Reachability analysis
Reachability analysis is a solution to the reachability problem in the particular context of distributed systems. It is used to determine which global states can be reached by a distributed system which consists of a certain number of local entities that communicated by the exchange of messages.
Overview
[edit]Reachability analysis was introduced in a paper of 1978 for the analysis and verification of communication protocols.[1] This paper was inspired by a paper by Bartlett et al. of 1968 [2] which presented the alternating bit protocol using finite-state modeling of the protocol entities, and also pointed out that a similar protocol described earlier had a design flaw. This protocol belongs to the Link layer and, under certain assumptions, provides as service the correct data delivery without loss nor duplication, despite the occasional presence of message corruption or loss.
For reachability analysis, the local entities are modeled by their states and transitions. An entity changes state when it sends a message, consumes a received message, or performs an interaction at its local service interface. The global state of a system with n entities [3] is determined by the states (i=1, ... n) of the entities and the state of the communication . In the simplest case, the medium between two entities is modeled by two FIFO queues in opposite directions, which contain the messages in transit (that are sent, but not yet consumed). Reachability analysis considers the possible behavior of the distributed system by analyzing all possible sequences of state transitions of the entities, and the corresponding global states reached.[4]
The result of reachability analysis is a global state transition graph (also called reachability graph) which shows all global states of the distributed system that are reachable from the initial global state, and all possible sequences of send, consume and service interactions performed by the local entities. However, in many cases this transition graph is unbounded and can not be explored completely. The transition graph can be used for checking general design flaws of the protocol (see below), but also for verifying that the sequences of service interactions by the entities correspond to the requirements given by the global service specification of the system.[1]
Protocol properties
[edit]Boundedness: The global state transition graph is bounded if the number of messages that may be in transit is bounded and the number states of all entities is bounded. The question whether the number of messages remains bounded in the case of finite state entities is in general not decidable.[5] One usually truncates the exploration of the transition graph when the number of messages in transit reaches a given threshold.
The following are design flaws:
- Global deadlock: The system is in a global deadlock if all entities wait for the consumption of a message and no message is in transit. Absence of global deadlocks can be verified by checking that no state in the reachability graph is a global deadlock.
- Partial deadlocks: An entity is in a deadlocked state if it waits for the consumption of a message and the system is in a global state where such a message is not in transit and will never be sent in any global state that can be reached in the future. Such a non-local property can be verified by performing model checking on the reachability graph.
- Unspecified reception: An entity has an unspecified reception if the next message to be consumed is not expected by the behavior specification of the entity in its current state. The absence of this condition can be verified by checking all states in the reachability graph.
An example
[edit]

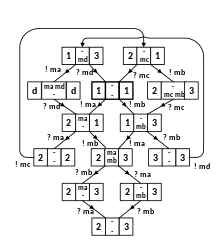
As an example, we consider the system of two protocol entities that exchange the messages ma, mb, mc and md with one another, as shown in the first diagram. The protocol is defined by the behavior of the two entities, which is given in the second diagram in the form of two state machines. Here the symbol "!" means sending a message, and "?" means consuming a received message. The initial states are the states "1".
The third diagram shows the result of the reachability analysis for this protocol in the form of a global state machine. Each global state has four components: the state of protocol entity A (left), the state of the entity B (right) and the messages in transit in the middle (upper part: from A to B; lower part: from B to A). Each transition of this global state machine corresponds to one transition of protocol entity A or entity B. The initial state is [1, - - , 1] (no messages in transit).
One sees that this example has a bounded global state space - the maximum number of messages that may be in transit at the same time is two. This protocol has a global deadlock, which is the state [2, - - , 3]. If one removes the transition of A in state 2 for consuming message mb, there will be an unspecified reception in the global states [2, ma mb ,3] and [2, - mb ,3].
Message transmission
[edit]The design of a protocol has to be adapted to the properties of the underlying communication medium, to the possibility that the communication partner fails, and to the mechanism used by an entity to select the next message for consumption. The communication medium for protocols at the Link level is normally not reliable and allows for erroneous reception and message loss (modeled as a state transition of the medium). Protocols using the Internet IP service should also deal with the possibility of out-of-order delivery. Higher-level protocols normally use a session-oriented Transport service which means that the medium provides reliable FIFO transmission of messages between any pair of entities. However, in the analysis of distributed algorithms, one often takes into account the possibility that some entity fails completely, which is normally detected (like a loss of message in the medium) by a timeout mechanism when an expected message does not arrive.
Different assumptions have been made about whether an entity can select a particular message for consumption when several messages have arrived and are ready for consumption. The basic models are the following:
- Single input queue: Each entity has a single FIFO queue where incoming messages are stored until they are consumed. Here the entity has no selection power and has to consume the first message in the queue.
- Multiple queues: Each entity has multiple FIFO queues, one for each communicating partner. Here the entity has the possibility to decide, depending on its state, from which queue (or queues) the next input message should be consumed.
- Reception pool: Each entity has a single pool where received messages are stored until they are consumed. Here the entity has the power to decide, depending on its state, which type of message should be consumed next (and wait for a message if none has been received yet), or possibly consume one from a set of message types (in order to deal with alternatives).
The original paper identifying the problem of unspecified receptions,[6] and much of the subsequent work, assumed a single input queue.[7] Sometimes, unspecified receptions are introduced by a race condition, which means that two messages are received and their order is not defined (which is often the case if they come from different partners). Many of these design flaws disappear when multiple queues or reception pools are used.[8] With the systematic use of reception pools, reachability analysis should check for partial deadlocks and messages remaining forever in the pool (without being consumed by the entity) [9]
Practical issues
[edit]Most of the work on protocol modeling use finite-state machines (FSM) to model the behavior of the distributed entities (see also Communicating finite-state machines). However, this model is not powerful enough to model message parameters and local variables. Therefore often so-called extended FSM models are used, such as supported by languages like SDL or UML state machines. Unfortunately, reachability analysis becomes much more complex for such models.
A practical issue of reachability analysis is the so-called ″state space explosion″. If the two entities of a protocol have 100 states each, and the medium may include 10 types of messages, up to two in each direction, then the number of global states in the reachability graph is bound by the number 100 x 100 x (10 x 10) x (10 x 10) which is 100 million. Therefore a number of tools have been developed to automatically perform reachability analysis and model checking on the reachability graph. We mention only two examples: The SPIN model checker and a toolbox for the construction and analysis of distributed processes.
Further reading
[edit]- Communication protocols
- Gerald Holzmann: Design and Validation of Computer Protocols, Prentice Hall, 1991.
- G.v. Bochmann, D. Rayner and C.H. West: Some notes on the history of protocol engineering, Computer Networks journal, 54 (2010), pp 3197–3209.
References and notes
[edit]- ^ a b Bochmann, G.v. "Finite State Description of Communication Protocols, Computer Networks, Vol. 2 (1978), pp. 361-372".
{{cite journal}}: Cite journal requires|journal=(help) - ^ K.A. Bartlett, R.A. Scantlebury and P.T. Wilkinson, A note on reliable full-duplex transmission over half- duplex links, C.ACM 12, 260 (1969).
- ^ Note: In the case of protocol analysis, there are normally only two entities.
- ^ Note: The corruption or loss of a message is modeled as a state transition of the .
- ^ M.G.Gouda, E.G.Manning, Y.T.Yu: On the progress of communication between two finite state machines, doi
- ^ P. Zafiropulo, C. West, H. Rudin, D. Cowan, D. Brand : Towards analyzing and synthesizing protocols, IEEE Transactions on Communications ( Volume: 28, Issue: 4, Apr 1980 )
- ^ Note: The SAVE construct of SDL can be used to indicate that certain types of messages should not be consumed in the current state, but saved for future processing.
- ^ M.F. Al-hammouri and G.v. Bochmann : Realizability of service specifications, Proc. System Analysis and Modelling (SAM) conference 2018, Copenhagen, LNCS, Springer
- ^ C. Fournet, T. Hoare, S. K. Rajamani, and J. Rehof : Stuck-free Conformance, Proc. 16th Intl. Conf. on Computer Aided Verification (CAV’04), LNCS, vol. 3114, Springer, 2004



