Risch algorithm

The Risch algorithm, named after Robert H. Risch, is an algorithm for the calculus operation of indefinite integration (i.e., finding antiderivatives). The algorithm transforms the problem of integration into a problem in algebra. It is based on the form of the function being integrated and on methods for integrating rational functions, radicals, logarithms, and exponential functions. Risch, who developed the algorithm in 1968, called it a decision procedure, because it is a method for deciding if a function has an elementary function as an indefinite integral; and also, if it does, determining it. The Risch algorithm is summarized (in more than 100 pages) in "Algorithms for Computer Algebra" by Keith O. Geddes, Stephen R. Czapor and George Labahn. The Risch–Norman algorithm, a faster but less powerful technique, was developed in 1976.

Description

The Risch algorithm is used to integrate elementary functions. These are functions obtained by composing exponentials, logarithms, radicals, trigonometry, and the four arithmetic operations (+ − × ÷). Laplace solved this problem for the case of rational functions, as he showed that the indefinite integral of a rational function is a rational function and a finite number of constant multiples of logarithms of rational functions. The algorithm suggested by Laplace is usually described in calculus textbooks; as a computer program it was finally implemented in the 1960s.

Liouville formulated the problem solved by the Risch algorithm. Liouville proved by analytical means that if there is an elementary solution g to the equation g ′ = f then for constants α_i and elementary functions u_i and v the solution is of the form

$g=v+\sum _{i<n}\alpha _{i}\,\ln(u_{i})$

Risch developed a method that allows one to only consider a finite set of elementary functions of Liouville's form.

The intuition for the Risch algorithm comes from the behavior of the exponential and logarithm functions under differentiation. For the function f e^g, where f and g are differentiable functions, we have

$(f\cdot e^{g})'=(f^{\prime }+f\cdot g^{\prime })\cdot e^{g},\,$

so if e^g were in the result of an indefinite integration, it should be expected to be inside the integral. Also, as

$(f\cdot \ln ^{n}g)'=f^{\prime }\ln ^{n}{g}+nf{\frac {g^{\prime }}{g}}\ln ^{n-1}{g}$

then if lnⁿg were in the result of an integration, then only a few powers of the logarithm should be expected.

Problem examples

Finding an elementary antiderivative is very sensitive to details. For instance, the following function has an elementary antiderivative:

$f(x)={\frac {x}{\sqrt {x^{4}+10x^{2}-96x-71}}}.$

But if 71 is changed to 72, it is not possible to represent the antiderivative using elementary functions. The reason is that the Galois group of

$x^{4}+10x^{2}-96x-71\,$

is D(4), e.g. generated by permutations (1 2 3 4) and (1 3), and contains 8 elements (same as in x⁴ − 2), while the Galois group of

$x^{4}+10x^{2}-96x-72\,$

is S(4), e.g. generated by permutations (1 2), (1 3), (1 4), and contains 24 elements.

Implementation

Transforming the Risch decision procedure into an algorithm that can be executed by a computer is a complex task that requires the use of heuristics and many refinements. No software (as of March 2008) is known to implement the full Risch algorithm, although several computer algebra systems have partial implementations. The only software that claims it has implemented in full the negative part is Axiom (i.e. if Axiom says "no" this means the antiderivative cannot be represented in terms of elementary functions, but in many cases Axiom says "error").

For example, of all known programs, only Axiom (see gallery), Mathematica and WolframAlpha (see [1]) can find an elementary antiderivative for the following function:

$f(x)={\frac {x}{\sqrt {x^{4}+10x^{2}-96x-71}}}$

The solution returned by Axiom is:

${\begin{aligned}F(x)=-{\frac {1}{8}}\ln &\,{\Big (}(x^{6}+15x^{4}-80x^{3}+27x^{2}-528x+781){\sqrt {x^{4}+10x^{2}-96x-71}}{\Big .}\\&-{\Big .}(x^{8}+20x^{6}-128x^{5}+54x^{4}-1408x^{3}+3124x^{2}+10001){\Big )}+C.\end{aligned}}$

Many programs can find the antiderivative for the above function using non-elementary functions (i.e. elliptic integrals, which are outside the scope of the Risch algorithm).

The following function is a more complex example, which most software cannot find an elementary antiderivative for:

$f(x)={\frac {x^{2}+2x+1+(3x+1){\sqrt {x+\ln x}}}{x\,{\sqrt {x+\ln x}}(x+{\sqrt {x+\ln x}})}}$

In fact, the antiderivative of this function has a fairly short form:

$F(x)=2({\sqrt {x+\ln x}}+\ln(x+{\sqrt {x+\ln x}}))+C.$

Decidability

The Risch algorithm applied to general elementary functions is not an algorithm but a semi-algorithm because it needs to check, as a part of its operation, if certain expressions are equivalent to zero (constant problem), in particular in the constant field. For expressions that involve only functions commonly taken to be elementary it is not known whether an algorithm performing such a check exists or not (current computer algebra systems use heuristics); moreover, if one adds the absolute value function to the list of elementary functions, it is known that no such algorithm exists; see Richardson's theorem.

Note that this issue also arises in the polynomial division algorithm; this algorithm will fail if it cannot correctly determine whether coefficients vanish identically. Therefore, the Risch algorithm too requires that the constant field be computable, i.e., that for elements not dependent on x, the problem of zero-equivalence is decidable.

Gallery

• 
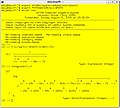
  Axiom computing the integral

See also

• Lists of integrals
• Liouville's theorem (differential algebra)
• Symbolic integration
• Axiom (computer algebra system)
• Incomplete Gamma function

References

• R. H. Risch (1969). "The problem of integration in finite terms". Transactions of the American Mathematical Society. 139. American Mathematical Society: 167–189. doi:10.2307/1995313.. http://www.ams.org/bull/1970-76-03/S0002-9904-1970-12455-7/S0002-9904-1970-12455-7.pdf
• R. H. Risch (1970). "The solution of the problem of integration in finite terms". Bulletin of the American Mathematical Society. 76 (3): 605–608. doi:10.1090/S0002-9904-1970-12454-5. AMS page PDF document
• Maxwell Rosenlicht (1972). "Integration in finite terms". American Mathematical Monthly. 79 (9). Mathematical Association of America: 963–972. doi:10.2307/2318066.
• Geddes, Czapor, Labahn (1992). Algorithms for Computer Algebra. Kluwer Academic Publishers. ISBN 0-7923-9259-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Manuel Bronstein (2005). Symbolic Integration I. Springer. ISBN 3-540-21493-3.
• Manuel Bronstein (1998). "Symbolic Integration Tutorial" (PDF). {{cite journal}}: Cite journal requires |journal= (help)
• Bhatt, Bhuvanesh. "Risch Algorithm". MathWorld.