Rule of Sarrus
In matrix theory, the rule of Sarrus is a mnemonic device for computing the determinant of a matrix named after the French mathematician Pierre Frédéric Sarrus.[1]
Consider a matrix
then its determinant can be computed by the following scheme.
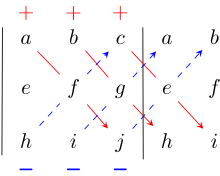
Write out the first two columns of the matrix to the right of the third column, giving five columns in a row. Then add the products of the diagonals going from top to bottom (solid) and subtract the products of the diagonals going from bottom to top (dashed). This yields[1][2]

A similar scheme based on diagonals works for matrices:[1]
Both are special cases of the Leibniz formula, which however does not yield similar memorization schemes for larger matrices. Sarrus' rule can also be derived using the Laplace expansion of a matrix.[1]
Another way of thinking of Sarrus' rule is to imagine that the matrix is wrapped around a cylinder, such that the right and left edges are joined.
References[edit]
- ^ a b c d Fischer, Gerd (1985). Analytische Geometrie (in German) (4th ed.). Wiesbaden: Vieweg. p. 145. ISBN 3-528-37235-4.
- ^ Paul Cohn: Elements of Linear Algebra. CRC Press, 1994, ISBN 9780412552809, p. 69
External links[edit]
- Sarrus' rule at Planetmath
- Linear Algebra: Rule of Sarrus of Determinants at khanacademy.org





