Serpentiles
Serpentiles is the name coined by Kurt N. Van Ness for the hexagonal tiles used in various edge-matching puzzle connection abstract strategy games, such as Psyche-Paths, Kaliko, and Tantrix.[1] For each tile, one to three colors are used to draw paths linking the six sides together in various configurations. Each side is connected to another side by a specific path route and color. Gameplay generally proceeds so that players take turns laying down tiles. During each turn, a tile is laid adjacent to existing tiles so that colored paths are contiguous across tile edges.
Serpentiles is also the name of a single-player puzzle connection game developed by Brett J. Gilbert and published by ThinkFun in 2008. The Serpentiles (2008) game includes square (1×1) and rectangular (2×1) tiles and challenge cards which provide a list of tiles that should be arranged to make a contiguous path.
Tile notation
[edit]Van Ness also coined a three-digit notation for tile categories, based on the paths shown on the tiles. The notation xyz refers to:[2]
- x = number of paths linking sides with adjacency 3, 2 segments apart (opposite sides)
- y = number of paths linking sides with adjacency 2, 1 segment apart
- z = number of paths linking sides with adjacency 1, 0 segments apart (adjacent sides)
It should be clear that adjacency 3 is the maximum. Because there are six sides, there are three paths between the sides, and the sum of the digits in the notation is always three. Van Ness also published a mathematical description: where is the count of segments with adjacency .[2] There are five distinct combinations of six sides and three paths,[3] ignoring for now the possibility of changing path color:
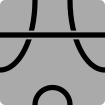
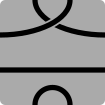
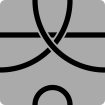
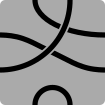
- 6S3P: Six-sided polygons with three paths
-
003, indicating the paths link three adjacent sides
-
021, indicating the paths link one adjacent side and two sides one segment apart
-
102, indicating the paths link two adjacent sides and one set of opposite sides
-
120, indicating the paths link two sides one segment apart and one set of opposite sides
-
300, indicating the paths link the complete set of three opposite sides
Rotational position
[edit]An orthogonal rotation that leaves the hexagon in the same orientation (with flat sides to the left and right) is 60°. There are six potential orthogonal rotational positions (360°/60°) of the regular six-sided hexagon. By examination, 300 has rotational symmetry: any rotation of 60° will result in the same sides being linked, so 0300 has one unique rotational position. Similarly, 003 has two unique rotational positions; one rotation of 60° will result in different sides being linked by the paths, but a second rotation of 60° in the same direction will result in the original sides being linked again. In a similar fashion, 102 and 120 both have three unique rotational positions, and 021 has six unique rotational positions.
To uniquely describe each rotational position, imagine a reference frame is applied where each side is numbered from 1 to 6 sequentially anti-clockwise. The paths connecting sides can be described as linked pairs.
For example, for 003 above, proceeding anti-clockwise from the lower right edge, the path/pair notation is 12-34-56. A single orthogonal rotation of the shape will add one (if anti-clockwise) or subtract one (if clockwise) to each number, modulo 6. In this way, the linked paths with an orthogonal rotation (60°) anti-clockwise would change to 23-45-67, or rewriting using modulo 6, 23-45-61, demonstrating that different sides are linked with a single orthogonal rotation. The specific order within a pair and the order in which the pairs are written does not affect the configuration. For example, 23-45-61 is equivalent to 23-45-16 and 16-23-45. Thus with a second orthogonal rotation, which results in 34-56-12, it is simple to demonstrate the second orthogonal rotation is equivalent to 12-34-56, the original orientation.
The reference frame could also be numbered sequentially in a clockwise fashion. In that case, a clockwise rotation would increment the values by 1, while an anti-clockwise rotation would decrement the values by 1. The orientation of the reference frame (clockwise or anti-clockwise) only affects the arithmetic required to rotate the tile. Likewise, the choice of origin (which side is designated the first side) for the reference frame is arbitrary, but the reference frame remains fixed during rotation.
| Class | Unique rotational positions |
Gallery of positions |
|---|---|---|
| 003 | 2 |
|
| 021 | 6 |
|
| 102 | 3 |
|
| 120 | 3 |
|
| 300 | 1 |
|
Describing the tiles by linked sides also implicitly includes the three-digit Van Ness notation. For any arbitrary three-pair sequence AB-CD-EF, the Van Ness notation can be recovered by the following formula:
Regular 4-sided square
[edit]Although a regular six-sided polygon (hexagon) can be used to cover a plane surface without gaps, a regular four-sided polygon (square) also can be used. The square with two paths linking sides can be described in a similar fashion, using a two-digit notation yz; there are just two potential configurations.[3]
- 4S2P: Four-sided polygons with two paths
-
02, indicating the paths link two adjacent sides
-
20, indicating the paths link two opposite sides
Like the hexagonal case, 20 (where all paths link opposite sides) has rotational symmetry. It is clear that 02 does not have rotational symmetry, as rotating the tile 90° clockwise or anti-clockwise will link different sides. Compare ![]() with the same tile rotated by 90°:
with the same tile rotated by 90°: ![]() Square tiles that lack rotational symmetry are known as Truchet tiles, as described in a 1704 memoir by Sébastien Truchet entitled "Mémoire sur les combinaisons" and popularized in 1987 by Cyril Stanley Smith.[4][5]
Square tiles that lack rotational symmetry are known as Truchet tiles, as described in a 1704 memoir by Sébastien Truchet entitled "Mémoire sur les combinaisons" and popularized in 1987 by Cyril Stanley Smith.[4][5]
Regular 8-sided octagon
[edit]Likewise, a regular eight-sided polygon (octagon) can have four paths pairing the eight sides, described using Van Ness's notation in a similar way with a four digit notation wxyz. There are 18 distinct combinations:[3]
- 8S4P: Eight-sided polygons with four paths
-
0004
-
0022
-
0040
-
0103
-
0121(a)
-
0121(b)
-
0202
-
0220
-
0301
-
0400
-
1012
-
1111(a)
-
1111(b)
-
1210
-
2002
-
2020
-
2200
-
4000
As with the preceding hexagon and square examples, the case linking all the opposite sides (4000) has rotational symmetry. Note that for the octagon, the notation no longer uniquely describes the path configuration. There are two duplicate notations in the gallery: 0121 and 1111. The 1111 pair are mirror-images. The rotational position notation can be applied to distinguish these tiles; with a reference frame numbered anti-clockwise starting from the bottom edge, 0121(a) above can be written as "0121 12-36-47-68", which is distinct from 0121(b): "0121 12-38-46-57". Likewise, 1111(a) is "1111 12-36-48-57", distinct from 1111(b): "1111 13-25-48-67". Using modular arithmetic (modulo 8), 1111(a) and (b) can each be rotated by one orthogonal rotation (45°) anti-clockwise to positions "15-24-36-78" and "15-68-47-23", respectively, demonstrating their paired reflective symmetry.
These octagonal tiles could be combined with the square tiles described here (rotated through 45° to fill the interstitial spaces) to completely tile a surface with paths across all edges.[6]
Regular polygons with 2 entry points per side
[edit]The preceding discussion covered the cases of regular 4-, 6-, and 8-sided polygons with a single entry point per side, with each side linked by a path. Because the paths link two different sides, using a single entry point per side requires regular 2n-sided polygons with an even number of sides to ensure that all entry points are linked by paths. If there are tiles with an odd number of sides, an even number of entry points would similarly ensure that all entry points are linked by paths.
- 3S3P: Three-sided polygons with three paths
-
003(a) 12-34-56
-
003(b) 16-23-45
-
021(a) 12-35-46
-
021(b) 13-26-45
-
102 12-36-45
-
120 15-24-36
-
300 14-25-36

For example, a regular 3-sided polygon (equilateral triangle) could have 2 entry points per side. There are 7 potential combinations using 3 paths per tile, depicted above.[3] Although the Van Ness notation can be applied by modifying it to count adjacency rather than sides, each tile is not uniquely described by the Van Ness notation, although the relationship between the 003(a) and (b) cases can be seen by inscribing a triangle, as the example shown here. A similar triangle could be inscribed for the 021(a) case to demonstrate its relationship to 021(b).
It may be simpler to describe the tile by path pairings instead. In the set of three-sided tiles with two entry points per side and three paths, the numbering starts from the left-hand point on the bottom edge and proceeds sequentially anti-clockwise.
One complete rotation turns the tile by 120° (=360°/3 sides). Rotation arithmetic is performed by adding two, modulo six. Consider the tile (12-34-56). Rotating the tile one or more complete rotations will, by inspection, not change the points that are linked. To demonstrate this, one rotation anti-clockwise results in the configuration (34-56-78), or, after the modulo arithmetic is performed, (34-56-12), which can be rearranged to (12-34-56), showing that one rotation does not affect the linked paths and so there is one distinct rotational position for this tile. On the other hand, consider the tile (13-26-45). The first two anti-clockwise rotations of this tile result in the configurations (16-24-35) and (15-23-46), respectively, so this tile has three distinct rotational positions.
Similarly, a regular 4-sided polygon (square) with 2 entry points per side has 35 potential combinations using 4 paths per tile.[3] The complete rotation is 90° and the rotational symmetry can be determined by adding 2, modulo 8 in a manner similar to that for the equilateral triangle case above. This set of four-sided polygons with two entry points per side and four paths per tile is used in the commercial board game Tsuro.
- 4S4P: Four-sided polygons with four paths
-
0004(a) 12-34-56-78
-
0004(b) 18-23-45-67
-
0022(a) 12-34-57-68
-
0022(b) 18-23-46-57
-
0040(a) 17-24-35-68
-
0040(b) 17-28-35-46
-
0103(a) 12-34-58-67
-
0103(b) 12-38-45-67
-
0121(a) 12-35-47-68
-
0121(b) 17-23-46-58
-
0121(x) 12-38-46-57
-
0121(y) 17-28-36-45
-
0202(a) 12-38-47-56
-
0202(b) 18-27-36-45
-
0220(a) 16-28-35-47
-
0220(b) 17-24-36-58
-
0301(a) 12-36-47-58
-
0301(b) 16-23-47-58
-
0400(a) 14-27-36-58
-
0400(b) 16-25-38-47
-
1012(a) 12-35-48-67
-
1012(b) 12-37-45-68
-
1111(a) 16-28-37-45
-
1111(b) 13-25-48-67
-
1111(x) 12-36-48-57
-
1111(y) 12-37-46-58
-
1210(a) 13-26-47-58
-
1210(b) 15-28-36-47
-
2002(a) 12-37-48-56
-
2002(b) 18-26-37-45
-
2020(a) 13-26-48-57
-
2020(b) 15-28-37-46
-
2200(a) 16-25-37-48
-
2200(b) 15-27-36-48
-
4000 15-26-37-48
In some cases, the (a) and (b) [or (a) and (x)] pairings can be recovered by inscribing a square in similar fashion. In other cases, the [(a) & (b)] or [(x) & (y)] sets are mirror-image pairs.
Generalization to regular polygons
[edit]For the general case where the tiles are n-sided regular polygons with m entry points per side so the product of n and m is even, the number of distinct combinations can be computed as .[3]
- is Euler's totient function, where
- is a conditional function defined as:
For example, a 10-sided decagon with a single path per side (5 paths total) has 105 combinations.[3]
| m Entry points per side | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| n Number of sides | 0 (circle) | 1 | 1 | 2 | 5 | 18 | ||||
| 1 (monogon) | 1 | 1 | 3 | 15 | 105 | |||||
| 2 (digon) | 1 | 1 | 3 | 11 | 65 | 513 | 5363 | 68219 | N/C | |
| 3 (triangle) | 1 | 7 | 3483 | N/C | N/C | |||||
| 4 (square) | 1 | 2 | 35 | 2688 | 508277 | N/C | N/C | N/C | N/C | |
| 5 (pentagon) | 1 | 193 | N/C | N/C | N/C | |||||
| 6 (hexagon) | 1 | 5 | 1799 | N/C | N/C | N/C | N/C | N/C | N/C | |
| 7 (heptagon) | 1 | 19311 | N/C | N/C | N/C | |||||
| 8 (octagon) | 1 | 18 | 254143 | N/C | N/C | N/C | N/C | N/C | N/C | |
| 9 (nonagon) | 1 | N/C | N/C | N/C | N/C | |||||
| 10 (decagon) | 1 | 105 | N/C | N/C | N/C | N/C | N/C | N/C | N/C | |
(Many of the values from the original source are N/C, meaning not computed)[3]
Variations
[edit]| Name | Year | Path colors | Tile material | Tile count | Notes | ||
|---|---|---|---|---|---|---|---|
| Psyche-Paths | 1969 | 3 | Cardboard | 85 + 6 blank | |||
| Kaliko | early 1980s | 3 | Lucite | (clear) | 85 | Lucite pieces until 2001. Current printing uses bamboo/wooden tiles. | |
| Wood | |||||||
| Tantrix | 1988 | 4 | Plastic | 56 | Up to three colors appear on a single tile. Tiles are numbered on the reverse. Triple Cross tiles not used. | ||
Psyche-Paths
[edit]A game of Psyche-Paths requires one to six players. Players take turns laying down tiles. Each tile laid down next to tiles that have already been laid must continue the color of the path(s) on the existing adjacent edge(s). Six blank tiles are provided as "wild cards" and are considered to continue any adjacent path. One tile is drawn at the start of the game and placed in the middle of the playing field to "seed" the game.[7]
In "Beginner" Psyche-Paths, players draw one tile from a pool of face-down tiles when it is their turn. One point is awarded for each connected path. If the player is unable to play the tile or makes an illegal play, it is retained and the player is penalized a number of points equal to the number of paths running through the retained tile at the end of the game.[7]
In "Standard" Psyche-Paths, two to four players each draw a hand of six tiles at the start of the game. During each turn, players may play any or all of their tiles, replenishing to a hand of six tiles at the end of their turn from the pool of face-down tiles. When laying down tiles, points are awarded only when two or more ends of an existing path is connected. The player scores a number of points equal to the number of tiles containing the connected color path. Three points are awarded if the path crosses itself, and the score is doubled if the path is closed. No penalty is taken for leftover tiles.[7] "Classic" Psyche-Paths is similar to "Standard", but adds a rule that each move must result in a single path through all the tiles in that move.[7]
"Solitaire" Psyche-Paths does not have specific rules, but rather suggestions, such as building alternating rows of eight and nine pieces in length using legal moves.[7]
Other games using regular polygonal tiles
[edit]Square tiles are used in connection games such as the Black Path Game (with a single-colored path) and Trax (with two colored paths). Octagonal tiles with a single path color are used with interstitial spaces and a game board with pre-printed links for the game Octiles.[8][9]
The Serpentiles (2008) game was developed by Brett J. Gilbert[10] and published by ThinkFun in 2008.[11] The Serpentiles (2008) game includes 19 plastic tiles: 4 square (1×1) and 12 rectangular (2×1) tiles with one printed green or blue path on each, and 3 square (1×1) node tiles with coincident blue and green path termini. The 2008 game also includes 40 challenge cards which provide a list of tiles (including two of the nodes) to be arranged so that one contiguous path of each color is made.[12]
History
[edit]The original hex-tile edge-matching connection game, Psyche-Paths, was designed by Charles Titus and Craige Schensted and published in the 1960s[13] with the 85 unique tile combinations and 6 blank "wild cards" on cardboard tiles.[7] In a review, researchers noted the game "accommodates a wide variety of ages, interests, and playing styles ... [involving] a number of skills that are of special interest to teachers and parents."[14] Steve Titus, the son of Charles, reissued the game in the 1980s as Kaliko using screen-printed acrylic tiles under the family business Future Games. Kaliko was licensed to Kadon in 1986 with a switch to wood tiles after 2001.[15]
Tantrix was released in 1988 by inventor Mike McManaway using four of the five possible path combinations (using Van Ness's notation: 003, 021, 102, and 120, excluding 300) to create 56 unique tiles, each with three different colors chosen from a palette of four. The primary innovation of Tantrix is the encoding of numbers on the reverse side of the tiles, allowing subsets of the 56 to be used for solitary puzzles.[16]
Hex tile sets
[edit]The complete set of 85 tiles, assuming a combination of up to three distinct path colors per tile, is shown in the table below, organized by notation and number of colors.
Tantrix uses the subset of tiles with three different path colors exclusively, and excludes the 300 Triple Cross series. With four possible path colors in Tantrix, there are four different color combinations with three different path colors, which gives 56 unique Tantrix tiles in a complete set:
- 003: 2 tiles with 3 path colors × 4 path color combinations = 8 Tantrix tiles in set 003
- 021: 6 tiles with 3 path colors × 4 path color combinations = 24 Tantrix tiles in set 021
- 102: 3 tiles with 3 path colors × 4 path color combinations = 12 Tantrix tiles in set 102
- 120: 3 tiles with 3 path colors × 4 path color combinations = 12 Tantrix tiles in set 120
References
[edit]- ^ Van Ness, Kurt N. "Serpentiles". van-ness.com. Retrieved 8 October 2017.
- ^ a b Van Ness, Kurt N. "Serpentile Descriptors". van-ness.com. Retrieved 8 October 2017.
- ^ a b c d e f g h i "Number of distinct Tsuro tiles which are square and have n points per side". The On-line Encyclopedia of Integer Sequences. July 9, 2014. Retrieved 31 May 2022.
- ^ Browne, Cameron (2008), "Truchet curves and surfaces", Computers & Graphics, 32 (2): 268–281, doi:10.1016/j.cag.2007.10.001.
- ^ Smith, Cyril Stanley (1987), "The tiling patterns of Sebastian Truchet and the topology of structural hierarchy", Leonardo, 20 (4): 373–385, doi:10.2307/1578535, JSTOR 1578535. With a translation of Truchet's text by Pauline Boucher.
- ^ Garrity, Mike (January 7, 2012). "Path Tile Games". From Here to There. Retrieved 31 May 2022.
- ^ a b c d e f "Psyche-Paths: Instructions". Funtastic, a Division of KMS Industries, Inc. 1969. Retrieved 8 October 2017.
- ^ O'Sullivan, Steffan (February 14, 1998). "Octiles, Designed by Dale Walton". Panix. Retrieved 26 May 2022.
- ^ "Octiles: Rules of play". Kadon Enterprises. Retrieved 26 May 2022.
- ^ "Serpentiles, published by ThinkFun". Brett J. Gilbert. Retrieved 23 September 2022.
- ^ "New ThinkFun Products for Spring of 2008" (Press release). ThinkFun. February 8, 2008. Retrieved 23 September 2022.
- ^ "Serpentiles from Thinkfun". The Puzzle Den [blog]. January 12, 201. Retrieved 23 September 2022.
- ^ Browne, Cameron (2005). "8: Connective Goal". Connection Games: Variations on a Theme. Boca Raton, Florida: CRC Press. p. 287. ISBN 978-1-56881-224-3. Retrieved 29 May 2022.
- ^ Parkis, Michael; Shea, Julia (1971). "Simulation Review". Simulation & Games. 2 (2): 233–236. doi:10.1177/003755007122009. hdl:2027.42/68407.
- ^ "Kaliko: Larger image and brief history". Kadon Games. November 2003. Retrieved 8 October 2017.
- ^ Browne, Cameron (2015). "Game Design Patterns: Explore the Design Space". Game & Puzzle Design. 1 (2). Raleigh, North Carolina: Lulu Press Inc: 75. ISBN 9781326494322. ISSN 2376-5097. Retrieved 8 October 2017.
External links
[edit]- Scherphuis, Jaap (2015). "Jaap's Puzzle Page: Tantrix". jaapsch.net. Retrieved 8 October 2017.


























![{\displaystyle 10^{[min(\left\vert B-A\right\vert ,6-\left\vert B-A\right\vert )-1]{\bmod {3}}}+10^{[min(\left\vert D-C\right\vert ,6-\left\vert D-C\right\vert )-1]{\bmod {3}}}+10^{[min(\left\vert F-E\right\vert ,6-\left\vert F-E\right\vert )-1]{\bmod {3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef7e2aa49fcde53816c9f668bd39d59a7eddaebc)