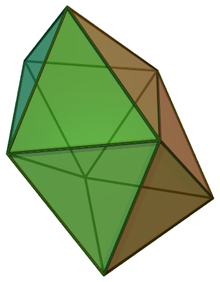
Snub disphenoid
| Snub disphenoid | |
|---|---|
 | |
| Type | Johnson J83 - J84 - J85 |
| Faces | 4+8 triangles |
| Edges | 18 |
| Vertices | 8 |
| Vertex configuration | 4(34) 4(35) |
| Symmetry group | D2d |
| Dual polyhedron | - |
| Properties | convex, deltahedron |
| Net | |
 | |
In geometry, the snub disphenoid, Siamese dodecahedron, or dodecadeltahedron is a three-dimensional convex polyhedron with twelve equilateral triangles as its faces. It is not a regular polyhedron because some vertices have four faces and others have five. It is a dodecahedron, one of the eight deltahedra (convex polyhedra with equilateral triangle faces) and one of the 92 Johnson solids (non-uniform convex polyhedra with regular faces).
History and naming
This shape was called a Siamese dodecahedron in the paper by Hans Freudenthal and B. L. van der Waerden (1947) which first described the set of eight convex deltahedra.[1] There are other simplicial dodecahedra, such as the hexagonal bipyramid, but this is the only one that can be realized with equilateral faces.
The dodecadeltahedron name was given to this shape by Bernal (1964), referring to the fact that it is a 12-sided deltahedron. Bernal was interested in the shapes of holes left in irregular close-packed arrangements of spheres, so he used a restrictive definition of deltahedra, in which a deltahedron is a convex polyhedron with triangular faces that can be formed by the centers of a collection of congruent spheres, whose tangencies represent polyhedron edges, and such that there is no room to pack another sphere inside the cage created by this system of spheres. This restrictive definition disallows the triangular bipyramid (as forming two tetrahedral holes rather than a single hole), pentagonal bipyramid (because the spheres for its apexes interpenetrate, so it cannot occur in sphere packings), and icosahedron (because it has interior room for another sphere). Bernal writes that the snub disphenoid is "a very common coordination for the calcium ion in crystallography".[2]
The snub disphenoid name comes from Norman Johnson's 1966 classification of the Johnson solids, convex polyhedra all of whose faces are regular.[3] As a Johnson solid, it is also given the notation J84.
Properties
The snub disphenoid is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the pentagonal bipyramid, and an irregular polyhedron with 12 vertices and 20 triangular faces.[4]
The snub disphenoid has the same symmetries as a tetragonal disphenoid: it has an axis of 180° rotational symmetry through the midpoints of its two opposite edges, two perpendicular planes of reflection symmetry through this axis, and four additional symmetry operations given by a reflection perpendicular to the axis followed by a quarter-turn and possibly another reflection parallel to the axis.[5] That is, it has D2d antiprismatic symmetry, a symmetry group of order 8.
Spheres centered at the vertices of the snub disphenoid form a cluster that, according to numerical experiments, has the minimum possible Lennard-Jones potential among all eight-sphere clusters.[6]
Up to symmetries and parallel translation, the snub disphenoid has five types of simple (non-self-crossing) closed geodesics. These are paths on the surface of the polyhedron that avoid the vertices and locally look like a shortest path: they follow straight line segments across each face of the polyhedron that they intersect, and when they cross an edge of the polyhedron they make complementary angles on the two incident faces to the edge. Intuitively, one could stretch a rubber band around the polyhedron along this path and it would stay in place: there is no way to locally change the path and make it shorter. For example, one type of geodesic crosses the two opposite edges of the snub disphenoid at their midpoints (where the symmetry axis exits the polytope) at an angle of π/3. A second type of geodesic passes near the intersection of the snub disphenoid with the plane that perpendicularly bisects the symmetry axis (the equator of the polyhedron), crossing the edges of eight triangles at angles that alternate between π/2 and π/6. Shifting a geodesic on the surface of the polyhedron by a small amount (small enough that the shift does not cause it to cross any vertices) preserves the property of being a geodesic and preserves its length, so both of these examples have shifted versions of the same type that are less symmetrically placed. The lengths of the five simple closed geodesics on a snub disphenoid with unit-length edges are
- (for the equatorial geodesic), , (for the geodesic through the midpoints of opposite edges), , and .
Except for the tetrahedron, which has infinitely many types of simple closed geodesic, the snub disphenoid has the most types of geodesic of any deltahedron.[7]
Construction
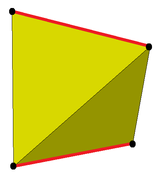
The snub disphenoid is constructed, as its name suggests, as the snub polyhedron formed from a tetragonal disphenoid, a lower symmetry form of a regular tetrahedron.
|

|
| Disphenoid | Snub disphenoid |
|---|
The snub operation produces a single cyclic band of triangles separating two opposite edges (red in the figure) and their adjacent triangles. The snub antiprisms are analogous in having a single cyclic band of triangles, but in the snub antiprisms these bands separate two opposite faces and their adjacent triangles rather than two opposite edges.
The snub disphenoid can also constructed from the square antiprism by replacing the two square faces by pairs of equilateral triangles. However, it is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.
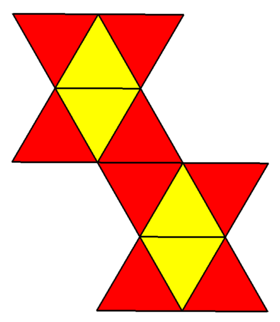
A physical model of the snub disphenoid can be formed by folding a net formed by 12 equilateral triangles (a 12-iamond), shown. An alternative net suggested by John Montroll has fewer concave vertices on its boundary, making it more convenient for origami construction.[8]
Coordinates
The eight vertices of the snub disphenoid may be given Cartesian coordinates
where the variables r, s, and t are algebraic numbers that can be expressed as follows. Let
and
where q is the positive real root of the cubic polynomial
Then
and
Because this construction involves the solution to a cubic equation, the snub disphenoid cannot be constructed with a compass and straightedge, unlike the other seven deltahedra.[9]
References
- ^ Freudenthal, H.; van d. Waerden, B. L. (1947), "On an assertion of Euclid", Simon Stevin, 25: 115–121, MR 0021687.
- ^ Bernal, J. D. (1964), "The Bakerian Lecture, 1962. The Structure of Liquids", Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 280 (1382): 299–322, JSTOR 2415872.
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- ^ Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), "On well-covered triangulations. III", Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002, MR 2602814.
- ^ Cundy, H. Martyn (1952), "Deltahedra", The Mathematical Gazette, 36: 263–266, doi:10.2307/3608204, MR 0051525.
- ^ a b Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H. (1995), "Minimal-energy clusters of hard spheres", Discrete and Computational Geometry, 14 (3): 237–259, doi:10.1007/BF02570704, MR 1344734.
- ^ Lawson, Kyle A.; Parish, James L.; Traub, Cynthia M.; Weyhaupt, Adam G. (2013), "Coloring graphs to classify simple closed geodesics on convex deltahedra.", International Journal of Pure and Applied Mathematics, 89 (2): 123–139, doi:10.12732/ijpam.v89i2.1, Zbl 1286.05048.
- ^ Montroll, John (2004), "Dodecadeltahedron", A Constellation of Origami Polyhedra, Dover Origami Papercraft Series, Dover Publications, Inc., pp. 38–40, ISBN 9780486439587.
- ^ Hartshorne, Robin (2000), Geometry: Euclid and Beyond, Undergraduate Texts in Mathematics, Springer-Verlag, p. 457, ISBN 9780387986500.








![{\displaystyle p={\sqrt[{3}]{-881+24i{\sqrt {237}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8bcef84b33cc2a254ad63b885e0c7a87ecbfd2b5)




