Well-covered graph

In graph theory, a well-covered graph is an undirected graph in which the minimal vertex covers all have the same size. Here, a vertex cover is a set of vertices that touches all edges, and it is minimal if removing any vertex from it would leave some edge uncovered. Equivalently, well-covered graphs are the graphs in which all maximal independent sets have equal size. Well-covered graphs were defined and first studied by Michael D. Plummer in 1970.
The well-covered graphs include all complete graphs, balanced complete bipartite graphs, and the rook's graphs whose vertices represent squares of a chessboard and edges represent moves of a chess rook. Known characterizations of the well-covered cubic graphs, well-covered claw-free graphs, and well-covered graphs of high girth allow these graphs to be recognized in polynomial time, but testing whether other kinds of graph are well-covered is a coNP-complete problem.
Definitions
[edit]A vertex cover in an undirected graph is a set of vertices that touches every edge in the graph. A vertex cover is minimal, or irredundant, if removing any vertex from it would destroy the covering property: the removal would cause some edge to become uncovered. It is minimum if there is no other vertex cover with fewer vertices. A well-covered graph is one in which every minimal cover is also minimum. In the original paper defining well-covered graphs, Plummer writes that this is "obviously equivalent" to the property that every two minimal covers have the same number of vertices as each other.[1]
An independent set in a graph is a set of vertices no two of which are adjacent to each other. If C is a vertex cover in a graph G, the complement of C must be an independent set, and vice versa. C is a minimal vertex cover if and only if its complement I is a maximal independent set, and C is a minimum vertex cover if and only if its complement is a maximum independent set. Therefore, a well-covered graph is, equivalently, a graph in which every maximal independent set has the same size, or a graph in which every maximal independent set is maximum.[2]
In the original paper defining well-covered graphs, these definitions were restricted to connected graphs,[3] although they are meaningful for disconnected graphs as well. Some later authors have replaced the connectivity requirement with the weaker requirement that a well-covered graph must not have any isolated vertices.[4] For both connected well-covered graphs and well-covered graphs without isolated vertices, there can be no essential vertices, vertices which belong to every minimum vertex cover. Additionally, every well-covered graph is a critical graph for vertex covering in the sense that, for every vertex v, deleting v from the graph produces a graph with a smaller minimum vertex cover.[3]
The independence complex of a graph G is the simplicial complex having a simplex for each independent set in G. A simplicial complex is said to be pure if all its maximal simplices have the same cardinality, so a well-covered graph is equivalently a graph with a pure independence complex.[5]
Examples
[edit]| a | b | c | d | e | f | g | h | ||
| 8 |  | 8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
A cycle graph of length four or five is well-covered: in each case, every maximal independent set has size two. A cycle of length seven, and a path of length three, are also well-covered.[6] Every complete graph is well-covered: every maximal independent set consists of a single vertex. Similarly, every cluster graph (a disjoint union of complete graphs) is well-covered.[7] A complete bipartite graph is well covered if the two sides of its bipartition have equal numbers of vertices, for these are its only two maximal independent sets. The complement graph of a triangle-free graph with no isolated vertices is well-covered: it has no independent sets larger than two, and every single vertex can be extended to a two-vertex independent set.[6]
A rook's graph is well covered: if one places any set of rooks on a chessboard so that no two rooks are attacking each other, it is always possible to continue placing more non-attacking rooks until there is one on every row and column of the chessboard.[8] The graph whose vertices are the diagonals of a simple polygon and whose edges connect pairs of diagonals that cross each other is well-covered, because its maximal independent sets are triangulations of the polygon and all triangulations have the same number of edges.[9]
If G is any n-vertex graph, then the rooted product of G with a one-edge graph (that is, the graph H formed by adding n new vertices to G, each of degree one and each adjacent to a distinct vertex in G) is well-covered. For, a maximal independent set in H must consist of an arbitrary independent set in G together with the degree-one neighbors of the complementary set, and must therefore have size n.[10] More generally, given any graph G together with a clique cover (a partition p of the vertices of G into cliques), the graph Gp formed by adding another vertex to each clique is well-covered; the rooted product is the special case of this construction when p consists of n one-vertex cliques.[11] Thus, every graph is an induced subgraph of a well-covered graph.
Bipartiteness, very well covered graphs, and girth
[edit]Favaron (1982) defines a very well covered graph to be a well-covered graph (possibly disconnected, but with no isolated vertices) in which each maximal independent set (and therefore also each minimal vertex cover) contains exactly half of the vertices. This definition includes the rooted products of a graph G and a one-edge graph. It also includes, for instance, the bipartite well-covered graphs studied by Ravindra (1977) and Berge (1981): in a bipartite graph without isolated vertices, both sides of any bipartition form maximal independent sets (and minimal vertex covers), so if the graph is well-covered both sides must have equally many vertices. In a well-covered graph with n vertices, without isolated vertices, the size of a maximum independent set is at most n/2, so very well covered graphs are the well covered graphs in which the maximum independent set size is as large as possible.[12]
A bipartite graph G is well-covered if and only if it has a perfect matching M with the property that, for every edge uv in M, the induced subgraph of the neighbors of u and v forms a complete bipartite graph.[13] The characterization in terms of matchings can be extended from bipartite graphs to very well covered graphs: a graph G is very well covered if and only if it has a perfect matching M with the following two properties:
- No edge of M belongs to a triangle in G, and
- If an edge of M is the central edge of a three-edge path in G, then the two endpoints of the path must be adjacent.
Moreover, if G is very well covered, then every perfect matching in G satisfies these properties.[14]
Trees are a special case of bipartite graphs, and testing whether a tree is well-covered can be handled as a much simpler special case of the characterization of well-covered bipartite graphs: if G is a tree with more than two vertices, it is well-covered if and only if each non-leaf node of the tree is adjacent to exactly one leaf.[13] The same characterization applies to graphs that are locally tree-like, in the sense that low-diameter neighborhoods of every vertex are acyclic: if a graph has girth eight or more (so that, for every vertex v, the subgraph of vertices within distance three of v is acyclic) then it is well-covered if and only if every vertex of degree greater than one has exactly one neighbor of degree one.[15] A closely related but more complex characterization applies to well-covered graphs of girth five or more.[16]
Regularity and planarity
[edit]

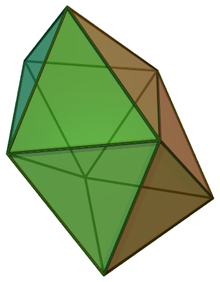
The cubic (3-regular) well-covered graphs have been classified: they consist of seven 3-connected examples, together with three infinite families of cubic graphs with lesser connectivity.[17]
The seven 3-connected cubic well-covered graphs are the complete graph K4, the graphs of the triangular prism and the pentagonal prism, the Dürer graph, the utility graph K3,3, an eight-vertex graph obtained from the utility graph by a Y-Δ transform, and the 14-vertex generalized Petersen graph G(7,2).[18] Of these graphs, the first four are planar graphs. They are the only four cubic polyhedral graphs (graphs of simple convex polyhedra) that are well-covered.[19] Four of the graphs (the two prisms, the Dürer graph, and G(7,2)) are generalized Petersen graphs.
The 1- and 2-connected cubic well-covered graphs are all formed by replacing the nodes of a path or cycle by three fragments of graphs which Plummer (1993) labels A, B, and C. Fragments A or B may be used to replace the nodes of a cycle or the interior nodes of a path, while fragment C is used to replace the two end nodes of a path. Fragment A contains a bridge, so the result of performing this replacement process on a path and using fragment A to replace some of the path nodes (and the other two fragments for the remaining nodes) is a 1-vertex-connected cubic well-covered graph. All 1-vertex-connected cubic well-covered graphs have this form, and all such graphs are planar.[17]
There are two types of 2-vertex-connected cubic well-covered graphs. One of these two families is formed by replacing the nodes of a cycle by fragments A and B, with at least two of the fragments being of type A; a graph of this type is planar if and only if it does not contain any fragments of type B. The other family is formed by replacing the nodes of a path by fragments of type B and C; all such graphs are planar.[17]
Complementing the characterization of well-covered simple polyhedra in three dimensions, researchers have also considered the well-covered simplicial polyhedra, or equivalently the well-covered maximal planar graphs. Every maximal planar graph with five or more vertices has vertex connectivity 3, 4, or 5.[20] There are no well-covered 5-connected maximal planar graphs, and there are only four 4-connected well-covered maximal planar graphs: the graphs of the regular octahedron, the pentagonal dipyramid, the snub disphenoid, and an irregular polyhedron (a nonconvex deltahedron) with 12 vertices, 30 edges, and 20 triangular faces. However, there are infinitely many 3-connected well-covered maximal planar graphs.[21] For instance, if a 3t-vertex maximal planar graph has t disjoint triangle faces, then these faces will form a clique cover. Therefore, the clique cover construction, which for these graphs consists of subdividing each of these t triangles into three new triangles meeting at a central vertex, produces a well-covered maximal planar graph.[22]
Complexity
[edit]Testing whether a graph contains two maximal independent sets of different sizes is NP-complete; that is, complementarily, testing whether a graph is well-covered is coNP-complete.[23] Although it is easy to find maximum independent sets in graphs that are known to be well-covered, it is also NP-hard for an algorithm to produce as output, on all graphs, either a maximum independent set or a guarantee that the input is not well-covered.[24]
In contrast, it is possible to test whether a given graph G is very well covered in polynomial time. To do so, find the subgraph H of G consisting of the edges that satisfy the two properties of a matched edge in a very well covered graph, and then use a matching algorithm to test whether H has a perfect matching.[14] Some problems that are NP-complete for arbitrary graphs, such as the problem of finding a Hamiltonian cycle, may also be solved in polynomial time for very well covered graphs.[25]
A graph is said to be equimatchable if every maximal matching is maximum; that is, it is equimatchable if its line graph is well-covered.[26] More strongly it is called randomly matchable if every maximal matching is a perfect matching. The only connected randomly matchable graphs are the complete graphs and the balanced complete bipartite graphs.[27] It is possible to test whether a line graph, or more generally a claw-free graph, is well-covered in polynomial time.[28]
The characterizations of well-covered graphs with girth five or more, and of well-covered graphs that are 3-regular, also lead to efficient polynomial time algorithms to recognize these graphs.[29]
Notes
[edit]- ^ Plummer (1970). Plummer uses "point" to mean a vertex in a graph, "line" to mean an edge, and "point cover" to mean a vertex cover; this terminology has fallen out of use.
- ^ Plummer (1993).
- ^ a b Plummer (1970).
- ^ Favaron (1982).
- ^ For examples of papers using this terminology, see Dochtermann & Engström (2009) and Cook & Nagel (2010).
- ^ a b Sankaranarayana (1994), Section 2.4, "Examples", p. 7.
- ^ Holroyd & Talbot (2005).
- ^ The rook's graphs are, equivalently, the line graphs of complete bipartite graphs, so the well-covered property of rook's graphs is equivalent to the fact that complete bipartite graphs are equimatchable, for which see Sumner (1979) and Lesk, Plummer & Pulleyblank (1984).
- ^ Greenberg (1993).
- ^ This class of examples was studied by Fink et al. (1985); they are also (together with the four-edge cycle, which is also well-covered) exactly the graphs whose domination number is n/2. Its well-covering property is also stated in different terminology (having a pure independence complex) as Theorem 4.4 of Dochtermann & Engström (2009).
- ^ For the clique cover construction, see Cook & Nagel (2010), Lemma 3.2. This source states its results in terms of the purity of the independence complex, and uses the term "fully-whiskered" for the special case of the rooted product.
- ^ Berge (1981).
- ^ a b Ravindra (1977); Plummer (1993).
- ^ a b Staples (1975); Favaron (1982); Plummer (1993).
- ^ Finbow & Hartnell (1983); Plummer (1993), Theorem 4.1.
- ^ Finbow & Hartnell (1983); Plummer (1993), Theorem 4.2.
- ^ a b c Campbell (1987); Campbell & Plummer (1988); Plummer (1993).
- ^ Campbell (1987); Finbow, Hartnell & Nowakowski (1988); Campbell, Ellingham & Royle (1993); Plummer (1993).
- ^ Campbell & Plummer (1988).
- ^ The complete graphs on 1, 2, 3, and 4 vertices are all maximal planar and well-covered; their vertex connectivity is either unbounded or at most three, depending on details of the definition of vertex connectivity that are irrelevant for larger maximal planar graphs.
- ^ Finbow, Hartnell, and Nowakowski et al. (2003, 2009, 2010).
- ^ The graphs constructed in this way are called the -family by Finbow et al. (2016); additional examples can be constructed by an operation they call an O-join for combining smaller graphs.
- ^ Sankaranarayana & Stewart (1992); Chvátal & Slater (1993); Caro, Sebő & Tarsi (1996).
- ^ Raghavan & Spinrad (2003).
- ^ Sankaranarayana & Stewart (1992).
- ^ Lesk, Plummer & Pulleyblank (1984).
- ^ Sumner (1979).
- ^ Lesk, Plummer & Pulleyblank (1984); Tankus & Tarsi (1996); Tankus & Tarsi (1997).
- ^ Campbell, Ellingham & Royle (1993); Plummer (1993).
References
[edit]- Berge, Claude (1981), "Some common properties for regularizable graphs, edge-critical graphs and B-graphs", Graph theory and algorithms (Proc. Sympos., Res. Inst. Electr. Comm., Tohoku Univ., Sendai, 1980), Lecture Notes in Computer Science, vol. 108, Berlin: Springer, pp. 108–123, doi:10.1007/3-540-10704-5_10, ISBN 978-3-540-10704-0, MR 0622929.
- Campbell, S. R. (1987), Some results on planar well-covered graphs, Ph.D. thesis, Vanderbilt University, Department of Mathematics. As cited by Plummer (1993).
- Campbell, S. R.; Ellingham, M. N.; Royle, Gordon F. (1993), "A characterisation of well-covered cubic graphs", Journal of Combinatorial Mathematics and Combinatorial Computing, 13: 193–212, MR 1220613.
- Campbell, Stephen R.; Plummer, Michael D. (1988), "On well-covered 3-polytopes", Ars Combinatoria, 25 (A): 215–242, MR 0942505.
- Caro, Yair; Sebő, András; Tarsi, Michael (1996), "Recognizing greedy structures", Journal of Algorithms, 20 (1): 137–156, doi:10.1006/jagm.1996.0006, MR 1368720.
- Chvátal, Václav; Slater, Peter J. (1993), "A note on well-covered graphs", Quo vadis, graph theory?, Annals of Discrete Mathematics, vol. 55, Amsterdam: North-Holland, pp. 179–181, MR 1217991.
- Cook, David II; Nagel, Uwe (2010), "Cohen-Macaulay graphs and face vectors of flag complexes", SIAM Journal on Discrete Mathematics, 26: 89–101, arXiv:1003.4447, Bibcode:2010arXiv1003.4447C, doi:10.1137/100818170.
- Dochtermann, Anton; Engström, Alexander (2009), "Algebraic properties of edge ideals via combinatorial topology", Electronic Journal of Combinatorics, 16 (2): Research Paper 2, doi:10.37236/68, MR 2515765.
- Favaron, O. (1982), "Very well covered graphs", Discrete Mathematics, 42 (2–3): 177–187, doi:10.1016/0012-365X(82)90215-1, MR 0677051.
- Finbow, A. S.; Hartnell, B. L. (1983), "A game related to covering by stars", Ars Combinatoria, 16 (A): 189–198, MR 0737090.
- Finbow, A.; Hartnell, B.; Nowakowski, R. (1988), "Well-dominated graphs: a collection of well-covered ones", Ars Combinatoria, 25 (A): 5–10, MR 0942485.
- Finbow, A.; Hartnell, B.; Nowakowski, R. J. (1993), "A characterization of well covered graphs of girth 5 or greater", Journal of Combinatorial Theory, Series B, 57 (1): 44–68, doi:10.1006/jctb.1993.1005, MR 1198396.
- Finbow, A.; Hartnell, B.; Nowakowski, R.; Plummer, Michael D. (2003), "On well-covered triangulations. I", Discrete Applied Mathematics, 132 (1–3): 97–108, doi:10.1016/S0166-218X(03)00393-7, MR 2024267.
- Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2009), "On well-covered triangulations. II", Discrete Applied Mathematics, 157 (13): 2799–2817, doi:10.1016/j.dam.2009.03.014, MR 2537505.
- Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), "On well-covered triangulations. III", Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002, MR 2602814.
- Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2016), "Well-covered triangulations: Part IV", Discrete Applied Mathematics, 215: 71–94, doi:10.1016/j.dam.2016.06.030, MR 3548980.
- Fink, J. F.; Jacobson, M. S.; Kinch, L. F.; Roberts, J. (1985), "On graphs having domination number half their order", Period. Math. Hungar., 16 (4): 287–293, doi:10.1007/BF01848079, MR 0833264, S2CID 121734811.
- Greenberg, Peter (1993), "Piecewise SL2Z geometry", Transactions of the American Mathematical Society, 335 (2): 705–720, doi:10.2307/2154401, JSTOR 2154401, MR 1140914.
- Holroyd, Fred; Talbot, John (2005), "Graphs with the Erdős-Ko-Rado property", Discrete Mathematics, 293 (1–3): 165–176, arXiv:math/0307073, doi:10.1016/j.disc.2004.08.028, MR 2136060.
- Lesk, M.; Plummer, M. D.; Pulleyblank, W. R. (1984), "Equi-matchable graphs", in Bollobás, Béla (ed.), Graph Theory and Combinatorics: Proceedings of the Cambridge Combinatorial Conference, in Honour of Paul Erdős, London: Academic Press, pp. 239–254, MR 0777180.
- Plummer, Michael D. (1970), "Some covering concepts in graphs", Journal of Combinatorial Theory, 8: 91–98, doi:10.1016/S0021-9800(70)80011-4, MR 0289347.
- Plummer, Michael D. (1993), "Well-covered graphs: a survey", Quaestiones Mathematicae, 16 (3): 253–287, doi:10.1080/16073606.1993.9631737, MR 1254158, archived from the original on May 27, 2012.
- Raghavan, Vijay; Spinrad, Jeremy (2003), "Robust algorithms for restricted domains", Journal of Algorithms, 48 (1): 160–172, doi:10.1016/S0196-6774(03)00048-8, MR 2006100, S2CID 16327087.
- Ravindra, G. (1977), "Well-covered graphs", Journal of Combinatorics, Information and System Sciences, 2 (1): 20–21, MR 0469831.
- Sankaranarayana, Ramesh S. (1994), Well-covered graphs: some new sub-classes and complexity results (Doctoral dissertation), University of Alberta
- Sankaranarayana, Ramesh S.; Stewart, Lorna K. (1992), "Complexity results for well-covered graphs", Networks, 22 (3): 247–262, CiteSeerX 10.1.1.47.9278, doi:10.1002/net.3230220304, MR 1161178.
- Staples, J. (1975), On some subclasses of well-covered graphs, Ph.D. thesis, Vanderbilt University, Department of Mathematics. As cited by Plummer (1993).
- Sumner, David P. (1979), "Randomly matchable graphs", Journal of Graph Theory, 3 (2): 183–186, doi:10.1002/jgt.3190030209, MR 0530304.
- Tankus, David; Tarsi, Michael (1996), "Well-covered claw-free graphs", Journal of Combinatorial Theory, Series B, 66 (2): 293–302, doi:10.1006/jctb.1996.0022, MR 1376052.
- Tankus, David; Tarsi, Michael (1997), "The structure of well-covered graphs and the complexity of their recognition problems", Journal of Combinatorial Theory, Series B, 69 (2): 230–233, doi:10.1006/jctb.1996.1742, MR 1438624.

