Supporting hyperplane

A convex set $S$ (in pink), a supporting hyperplane of $S$ (the dashed line), and the supporting half-space delimited by the hyperplane which contains $S$ (in light blue).

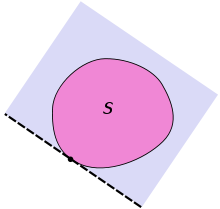
In geometry, a supporting hyperplane of a set $S$ in Euclidean space $\mathbb {R} ^{n}$ is a hyperplane that has both of the following two properties:

• $S$ is entirely contained in one of the two closed half-spaces bounded by the hyperplane,
• $S$ has at least one boundary-point on the hyperplane.

Here, a closed half-space is the half-space that includes the points within the hyperplane.

Supporting hyperplane theorem

A convex set can have more than one supporting hyperplane at a given point on its boundary.

This theorem states that if $S$ is a convex set in the topological vector space $X=\mathbb {R} ^{n},$ and $x_{0}$ is a point on the boundary of $S,$ then there exists a supporting hyperplane containing $x_{0}.$ If $x^{*}\in X^{*}\backslash \{0\}$ ($X^{*}$ is the dual space of $X$, $x^{*}$ is a nonzero linear functional) such that $x^{*}\left(x_{0}\right)\geq x^{*}(x)$ for all $x\in S$, then

$H=\{x\in X:x^{*}(x)=x^{*}\left(x_{0}\right)\}$

defines a supporting hyperplane.

Conversely, if $S$ is a closed set with nonempty interior such that every point on the boundary has a supporting hyperplane, then $S$ is a convex set, and is the intersection of all its supporting closed half-spaces.

The hyperplane in the theorem may not be unique, as noticed in the second picture on the right. If the closed set $S$ is not convex, the statement of the theorem is not true at all points on the boundary of $S,$ as illustrated in the third picture on the right.

The supporting hyperplanes of convex sets are also called tac-planes or tac-hyperplanes.

The forward direction can be proved as a special case of the separating hyperplane theorem (see the page for the proof). For the converse direction,

Proof

Define $T$ to be the intersection of all its supporting closed half-spaces. Clearly $S\subset T$. Now let $y\not \in S$, show $y\not \in T$.

Let $x\in \mathrm {int} (S)$, and consider the line segment $[x,y]$. Let $t$ be the largest number such that $[x,t(y-x)+x]$ is contained in $S$. Then $t\in (0,1)$.

Let $b=t(y-x)+x$, then $b\in \partial S$. Draw a supporting hyperplane across $b$. Let it be represented as a nonzero linear functional $f:\mathbb {R} ^{n}\to \mathbb {R}$ such that $\forall a\in T,f(a)\geq f(b)$. Then since $x\in \mathrm {int} (S)$, we have $f(x)>f(b)$. Thus by ${\frac {f(y)-f(b)}{1-t}}={\frac {f(b)-f(x)}{t-0}}<0$, we have $f(y)<f(b)$, so $y\not \in T$.

See also

A supporting hyperplane containing a given point on the boundary of $S$ may not exist if $S$ is not convex.

• Support function
• Supporting line (supporting hyperplanes in $\mathbb {R} ^{2}$)

References & further reading

• Ostaszewski, Adam (1990). Advanced mathematical methods. Cambridge; New York: Cambridge University Press. p. 129. ISBN 0-521-28964-5.

• Giaquinta, Mariano; Hildebrandt, Stefan (1996). Calculus of variations. Berlin; New York: Springer. p. 57. ISBN 3-540-50625-X.

• Goh, C. J.; Yang, X.Q. (2002). Duality in optimization and variational inequalities. London; New York: Taylor & Francis. p. 13. ISBN 0-415-27479-6.

• Soltan, V. (2021). Support and separation properties of convex sets in finite dimension. Extracta Math. Vol. 36, no. 2, 241-278.