Symmetric monoidal category

In category theory, a branch of mathematics, a symmetric monoidal category is a braided monoidal category that is maximally symmetric. That is, the braiding operator $s_{AB}$ obeys an additional identity: $s_{BA}\circ s_{AB}=1_{A\otimes B}$.

The classifying space (geometric realization of the nerve) of a symmetric monoidal category is an $E_\infty$ space, so its group completion is an infinite loop space.

Definition

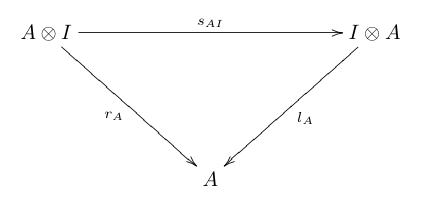
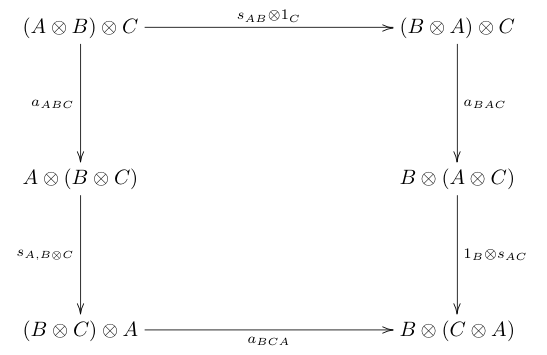
A symmetric monoidal category is a monoidal category (C, ⊗) such that, for every pair A, B of objects in C, there is an isomorphism $s_{AB}: A \otimes B \simeq B \otimes A$ that is natural in both A and B and such that the following diagrams commute:

• The unit coherence:

  

• The associativity coherence:

  

• The inverse law:

  

In the diagrams above, a, l , r are the associativity isomorphism, the left unit isomorphism, and the right unit isomorphism respectively.

Examples

The prototypical example is the category of vector spaces. Some examples and non-examples of symmetric monoidal categories:

• The category of sets. The tensor product is the set theoretic cartesian product, and any singleton can be fixed as the unit object.
• The category of groups. Like before, the tensor product is just the cartesian product of groups, and the trivial group is the unit object.
• More generally, a category with finite products, that is, a Cartesian monoidal category, is symmetric monoidal. The tensor product is the direct product of objects, and any terminal object (empty product) is the unit object.
• The category of bimodules over a ring R is monoidal, but not necessarily symmetric. If R is commutative, the category of left R-modules is symmetric monoidal.
• The dagger symmetric monoidal categories are symmetric monodal categories with an additional dagger structure.

A cosmos is a complete cocomplete closed symmetric monoidal category.

References

• Symmetric monoidal category in nLab
• This article incorporates material from Symmetric monoidal category on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.