Triangle wave

From Wikipedia, the free encyclopedia

A triangle wave is a non-sinusoidal waveform named for its triangular shape.

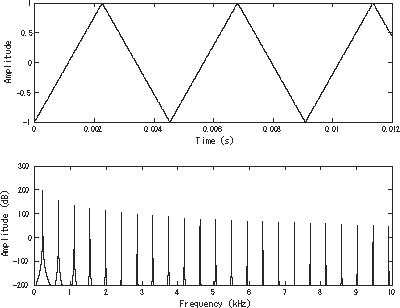A bandlimited triangle wave pictured in the time domain (top) and frequency domain (bottom). The fundamental is at 220 Hz (A2).

Like a square wave, the triangle wave contains only odd harmonics. However, the higher harmonics roll off much faster than in a square wave (proportional to the inverse square of the harmonic number as opposed to just the inverse).

It is possible to approximate a triangle wave with additive synthesis by adding odd harmonics of the fundamental, multiplying every (4n−1)th harmonic by −1 (or changing its phase by π), and rolling off the harmonics by the inverse square of their relative frequency to the fundamental.

This infinite Fourier series converges to the triangle wave:

$\begin{align} x_\mathrm{triangle}(t) & {} = \frac {8}{\pi^2} \sum_{k=0}^\infty (-1)^k \, \frac{ \sin \left(2\pi (2k+1)ft \right)}{(2k+1)^2} \\ & {} = \frac{8}{\pi^2} \left( \sin (2\pi ft)-{1 \over 9} \sin (6 \pi ft)+{1 \over 25} \sin (10 \pi ft) + \cdots \right) \end{align}$