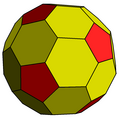
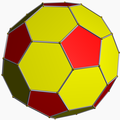
Chamfered dodecahedron

Truncated rhombic triacontahedron
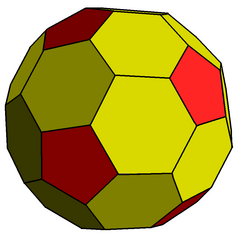
Type	Conway polyhedron
Faces	12 pentagons 30 hexagons
Edges	120 (2 types)
Vertices	80 (2 types)
Vertex configuration	(60) 5.6.6 (20) 6.6.6
Symmetry group	Icosahedral (Ih)
Dual polyhedron	-
Properties	convex, equilateral-faced

A net for truncated rhombic triacontahedron

The truncated rhombic triacontahedron is a convex polyhedron constructed from the rhombic triacontahedron by truncating the twelve vertices where five faces meet at their acute corners.

The 12 vertices can be truncated such that all edges are equal length. The original 30 rhombic faces become non-regular hexagons, and the truncated vertices become regular pentagons.

The hexagon faces can be equilateral but not regular with D₂ symmetry. The angles at the two vertices with vertex configuration 6.6.6 are arccos(-1/sqrt(5)) = 116.565 degrees, and at the remaining four vertices with 5.6.6, they are 121.717 degrees each.

Related polyhedra

This polyhedron looks very similar to the uniform truncated icosahedron which has 12 pentagons, but only 20 hexagons.

• 
  Truncated rhombic triacontahedron
• 
  Truncated icosahedron

Note that this name is ambiguous since only 12 vertices were truncated, and different polyhedra can be generated by truncating the other 20 vertices, or all 32 vertices of the original rhombic triacontahedron.

Chemistry

This is the shape of the fullerene C₈₀; sometimes this shape is denoted C₈₀(I_h) to describe its icosahedral symmetry and distinguish it from other less-symmetric 80-vertex fullerenes. It is one of only four fullerenes found by Deza, Deza & Grishukhin (1998) to have a skeleton that can be isometrically embeddable into an L₁ space.

References

• Deza, A.; Deza, M.; Grishukhin, V. (1998), "Fullerenes and coordination polyhedra versus half-cube embeddings", Discrete Mathematics, 192 (1): 41–80, doi:10.1016/S0012-365X(98)00065-X.

See also

• Truncated rhombic dodecahedron

External links

• VTML polyhedral generator Try "t5daD" (Conway polyhedron notation)
• Zometool model
• Fullerene C80
  1. [1] (Number 7 -Ih)
  2. [2]