Sphere eversion
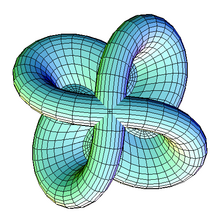


In differential topology, sphere eversion is the process of turning a sphere inside out in a three-dimensional space (the word eversion means "turning inside out"). It is possible to smoothly and continuously turn a sphere inside out in this way (allowing self-intersections of the sphere's surface) without cutting or tearing it or creating any crease. This is surprising, both to non-mathematicians and to those who understand regular homotopy, and can be regarded as a veridical paradox; that is something that, while being true, on first glance seems false.
More precisely, let
be the standard embedding; then there is a regular homotopy of immersions
such that ƒ0 = ƒ and ƒ1 = −ƒ.
History
[edit]An existence proof for crease-free sphere eversion was first created by Stephen Smale (1957). It is difficult to visualize a particular example of such a turning, although some digital animations have been produced that make it somewhat easier. The first example was exhibited through the efforts of several mathematicians, including Arnold S. Shapiro and Bernard Morin, who was blind. On the other hand, it is much easier to prove that such a "turning" exists, and that is what Smale did.
Smale's graduate adviser Raoul Bott at first told Smale that the result was obviously wrong (Levy 1995). His reasoning was that the degree of the Gauss map must be preserved in such "turning"—in particular it follows that there is no such turning of S1 in R2. But the degrees of the Gauss map for the embeddings f and −f in R3 are both equal to 1, and do not have opposite sign as one might incorrectly guess. The degree of the Gauss map of all immersions of S2 in R3 is 1, so there is no obstacle. The term "veridical paradox" applies perhaps more appropriately at this level: until Smale's work, there was no documented attempt to argue for or against the eversion of S2, and later efforts are in hindsight, so there never was a historical paradox associated with sphere eversion, only an appreciation of the subtleties in visualizing it by those confronting the idea for the first time.
See h-principle for further generalizations.
Proof
[edit]Smale's original proof was indirect: he identified (regular homotopy) classes of immersions of spheres with a homotopy group of the Stiefel manifold. Since the homotopy group that corresponds to immersions of in vanishes, the standard embedding and the inside-out one must be regular homotopic. In principle the proof can be unwound to produce an explicit regular homotopy, but this is not easy to do.
There are several ways of producing explicit examples and mathematical visualization:
- Half-way models: these consist of very special homotopies. This is the original method, first done by Shapiro and Phillips via Boy's surface, later refined by many others. The original half-way model homotopies were constructed by hand, and worked topologically but weren't minimal. The movie created by Nelson Max, over a seven-year period, and based on Charles Pugh's chicken-wire models (subsequently stolen from the Mathematics Department at Berkeley), was a computer-graphics 'tour de force' for its time, and set the bench-mark for computer animation for many years. A more recent and definitive graphics refinement (1980s) is minimax eversions, which is a variational method, and consist of special homotopies (they are shortest paths with respect to Willmore energy). In turn, understanding behavior of Willmore energy requires understanding solutions of fourth-order partial differential equations, and so the visually beautiful and evocative images belie some very deep mathematics beyond Smale's original abstract proof.
- Thurston's corrugations: this is a topological method and generic; it takes a homotopy and perturbs it so that it becomes a regular homotopy. This is illustrated in the computer-graphics animation Outside In developed at the Geometry Center under the direction of Silvio Levy, Delle Maxwell and Tamara Munzner.[2]
- Combining the above methods, the complete sphere eversion can be described by a set of closed equations giving minimal topological complexity [1]
Variations
[edit]- A six-dimensional sphere in seven-dimensional euclidean space admits eversion.[3] With an evident case of an 0-dimensional sphere (two distinct points) in a real line and described above case of a two-dimensional sphere in there are only three cases when sphere embedded in euclidean space admits eversion.
Gallery of eversion steps
[edit]
See also
[edit]References
[edit]- ^ a b Bednorz, Adam; Bednorz, Witold (2019). "Analytic sphere eversion using ruled surfaces". Differential Geometry and Its Applications. 64: 59–79. arXiv:1711.10466. doi:10.1016/j.difgeo.2019.02.004. S2CID 119687494.
- ^ "Outside In: Introduction". The Geometry Center. Retrieved 21 June 2017.
- ^ Goryunov, Victor V. (1997). "Local invariants of mappings of surfaces into three-space". The Arnold–Gelfand mathematical seminars. Boston, Massachusetts: Birkhäuser. pp. 223–255. ISBN 0-8176-3883-0.
Bibliography
[edit]- Iain R. Aitchison (2010) The `Holiverse': holistic eversion of the 2-sphere in R^3, preprint. arXiv:1008.0916.
- John B. Etnyre (2004) Review of "h-principles and flexibility in geometry", MR1982875.
- Francis, George K. (2007), A topological picturebook, Berlin, New York: Springer-Verlag, ISBN 978-0-387-34542-0, MR 2265679
- George K. Francis & Bernard Morin (1980) "Arnold Shapiro's Eversion of the Sphere", Mathematical Intelligencer 2(4):200–3.
- Levy, Silvio (1995), "A brief history of sphere eversions", Making waves, Wellesley, MA: A K Peters Ltd., ISBN 978-1-56881-049-2, MR 1357900
- Max, Nelson (1977) "Turning a Sphere Inside Out", https://www.crcpress.com/Turning-a-Sphere-Inside-Out-DVD/Max/9781466553941 Archived 2016-03-04 at the Wayback Machine
- Anthony Phillips (May 1966) "Turning a surface inside out", Scientific American, pp. 112–120.
- Smale, Stephen (1958), "A classification of immersions of the two-sphere", Transactions of the American Mathematical Society, 90 (2): 281–290, doi:10.2307/1993205, ISSN 0002-9947, JSTOR 1993205, MR 0104227
External links
[edit]- A History of Sphere Eversions Archived 2020-07-11 at the Wayback Machine
- "Turning a Sphere Inside Out"
- Software for visualizing sphere eversion
- Mathematics visualization: topology. The holiverse sphere eversion (Povray animation)
- The deNeve/Hills sphere eversion: video and interactive model
- Patrick Massot's project to formalise the proof in the Lean Theorem Prover
- An interactive exploration of Adam Bednorz and Witold Bednorz method of sphere eversion
- Outside In: A video exploration of sphere eversion, created by The Geometry Center of The University of Minnesota.