User:AndjelaVujovic/Рекурзивни алгоритам најмањих квадрата (RLS алгоритам)
Рекурзивни алгоритам најмањих квадрата (RLS) је адаптивни филтер који рекурзивно утврђује коефицијенте који смањују линеарни најмањи квадрат функција трошкова у вези улазних сигнала. Ово је за разликa у односу на друге алгоритме као што је алгоритам најмањих средњих квадрата (LMS) чији је циљ да смањи средње квадратне грешке. У извођење рекурзивног алгоритма најмањих квадрата, улазни сигнал се сматра детерминистичким, док се алгоритам најмањих средњих квадрата и слични алгоритми сматрају стохастичком. У поређењу са већином својих конкурената, експонати рекурзивног алгоритма најмањих квадрат изузетно брзо конвергирају. Међутим, ова корист долази по цену високог рачунарске комплексности.
Мотивација
[edit]RLS је открио Карл Фридрих Гаус али остаје неискоришћен или игнорисан до 1950. године, када Плацкет открива оригинални рад Гауса од 1821. У принципу, RLS алгоритми могу да се користе за решавање сваког проблема који могу да реше адаптивни филтери, На пример, претпоставимо да је сигнал d(n) који се преноси преко еха, бучни канал који узрокује да буде примљен као
где представља додатну буку. Ми ћемо покушати да опоравимо жељени сигнал употребом -tap импулса коначних одзива, :
где је вектор који садржи Најновији узорци . Наш циљ је да се процени параметре филтера , и у сваком тренутку n мислимо на нове најмањих квадрата процена . Како време пролази, желимо да се у потпуности избегну преправке алгоритма најмањих квадрата и да пронађу нову процену за , у смислу .
Корист од RLS алгоритма је да нема потребе обрнути матрицу, чиме се штеди рачунарска снага. Још једна предност је у томе што даје интуицију иза таквих резултата као Калман филтер.
Дискусија
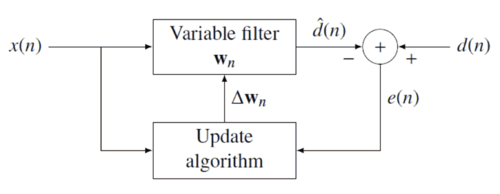
[edit]Идеја РЛС филтера је да се минимизира функцију трошкова адекватно избором филтер коефицијенти , ажурирање филтера као стиже нови подаци. Сигнал грешке <матх> и жељени сигнал су дефинисани у дијаграму негативне повратне спреге:
Грешка имплицитно зависи од коефицијента филтера путем процене :
Најмања функција квадрата грешка—желимо да се функција трошкова минимизира у функцији e(n) која такође зависи од коефицијента филтера:
где је "фактор заборављања" који даје експоненцијално мању тежину старијим узорцима грешака.
Функција трошкова је сведена на минимум узимањем парцијалних извода за све ставке коефицијената вектора и постављање резултата на нулу
Даље, замени са дефиницијом сигнала грешке
Преуређење једначине приноса
Овај образац може да се изрази у смислу матрице
- где је измерен узорак коваријанси матрица за , и је еквивалентна процена за попречну-коваријансу од и . На основу овог израза налазимо коефицијенте који минимизирају функцију трошкова као:
Ово је главни резултат дискусије.
Избор
[edit]Мањи је, мањи допринос претходних узорака. То чини филтера више осетљивији на недавним узорака, што значи више флуктуације у филтеру ко-еффициентс.The случај се као растућег прозор РЛС алгоритам . У пракси, је обично бира између 0,98 и 1. [1]
- ^ Emannual C. Ifeacor, Barrie W. Jervis.Дигитална обрада сигнала: практични приступ, друго издање. Индианаполис: Пеарсон Едуцатион Лимитед, 2002., стр. 718718







![{\displaystyle \mathbf {x} _{n}=[x(n)\quad x(n-1)\quad \ldots \quad x(n-p)]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09eb921b307dabe5f3f396085912215d09c02114)











![{\displaystyle \sum _{i=0}^{n}\lambda ^{n-i}\left[d(i)-\sum _{l=0}^{p}w_{n}(l)x(i-l)\right]x(i-k)=0\qquad k=0,1,\cdots ,p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f227f57b5708e2279ff63386d33c501f76f500b7)
![{\displaystyle \sum _{l=0}^{p}w_{n}(l)\left[\sum _{i=0}^{n}\lambda ^{n-i}\,x(i-l)x(i-k)\right]=\sum _{i=0}^{n}\lambda ^{n-i}d(i)x(i-k)\qquad k=0,1,\cdots ,p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43bb38e8f5f1fa0bb012d33ae44308679a9707c2)





