User:CrypticNfamous/Net force

Changes made:

In mechanics, the net force is the vector sum of all forces acting on a particle or object. It is a single force that replicates the effect of the original forces on the particle's motion, resulting in the same acceleration as all those actual forces combined, in accordance with Newton's second law of motion.

The associated torque of a net force can be determined, such that it continues the movement of parts of the object under the initial system of forces. This net force, along with its associated torque, becomes the resultant force. It affects the rotational motion of the object similarly to how all actual forces taken together would. In certain scenarios, a system of forces can define a resultant force that is free of torque. Here, the net force, when applied along the correct line of action, replicates the effect of all the forces at their respective points of application. However, it is not always possible to identify such a torque-free resultant force.

—----------------------------------------------------------------------------------------------------------------------------

The Concept of Total Force

An illustrative method for the addition of forces.

In physics, a force is considered a vector quantity. This means that it not only has a size (or magnitude) but also a direction in which it acts. We typically represent force with the symbol F in boldface, or sometimes, we place an arrow over the symbol to indicate its vector nature, like this: $\scriptstyle {\vec {F}}$.

When we need to visually represent a force, we draw a line segment. This segment starts at a point A, where the force is applied, and ends at another point B. This line not only gives us the direction of the force (from A to B) but also its magnitude: the longer the line, the stronger the force.

One of the essential concepts in physics is that forces can be added together, which is the basis of vector addition. This concept has been central to physics since the times of Galileo and Newton, forming the cornerstone of Vector calculus, which came into its own in the late 1800s and early 1900s.

The diagram on this page shows how to add two forces using the tip-to-tail method. This method involves drawing the first force, $\scriptstyle {\vec {F}}_{1}$, and then drawing the second force, $\scriptstyle {\vec {F}}_{2}$, starting from the tip of the first force. The resulting force, or 'total' force, $\scriptstyle {\vec {F}}$, is then drawn from the start of the first force (the tail) to the end of the second force (the tip).

Grasping this concept is fundamental to understanding how forces interact and combine to influence the motion and equilibrium of objects.

—----------------------------------------------------------------------------------------------------------------------------

When forces are applied to an extended body (a body that's not a single point), they can be applied at different points. Such forces are called 'bound vectors'. It's important to remember that to add these forces together, they need to be considered at the same point.

The concept of 'net force' comes into play when you look at the total effect of all these forces on the body. However, the net force alone may not necessarily preserve the motion of the body. This is because, besides the net force, the 'torque' or rotational effect associated with these forces also matters. The net force must be applied at the right point, and with the right associated torque, to replicate the effect of the original forces.

When the net force and the appropriate torque are applied at a single point, they together constitute what is known as the resultant force. This resultant force-and-torque combination will have the same effect on the body as all the original forces and their associated torques.

—----------------------------------------------------------------------------------------------------------------------------

In mechanics, the net force is the vector sum of forces acting on a particle or object. The net force is a single force that replaces the effect of the original forces on the particle's motion. It gives the particle the same acceleration as all those actual forces together as described by Newton's second law of motion.

It is possible to determine the torque associated with the point of application of a net force so that it maintains the movement of jets of the object under the original system of forces. Its associated torque, the net force, becomes the resultant force and has the same effect on the rotational motion of the object as all actual forces taken together. It is possible for a system of forces to define a torque-free resultant force. In this case, the net force, when applied at the proper line of action, has the same effect on the body as all of the forces at their points of application. It is not always possible to find a torque-free resultant force.

The Concept of Total Force

In physics, a force is considered a vector quantity. This means that it not only has a size (or magnitude) but also a direction in which it acts. We typically represent force with the symbol F in boldface, or sometimes, we place an arrow over the symbol to indicate its vector nature, like this: $\scriptstyle {\vec {F}}$.

When we need to visually represent a force, we draw a line segment. This segment starts at a point A, where the force is applied, and ends at another point B. This line not only gives us the direction of the force (from A to B) but also its magnitude: the longer the line, the stronger the force.

One of the essential concepts in physics is that forces can be added together, which is the basis of vector addition. This concept has been central to physics since the times of Galileo and Newton, forming the cornerstone of Vector calculus, which came into its own in the late 1800s and early 1900s.

Addition_af_vektorer

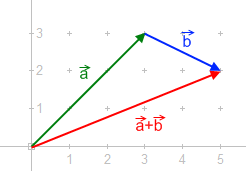
The picture to the right shows how to add two forces using the "tip-to-tail" method. This method involves drawing forces $\scriptstyle {\mathbf {\vec {a}}}$, and $\scriptstyle {\mathbf {\vec {b}}}$ from the tip of the first force. The resulting force, or 'total' force, $\scriptstyle {\vec {F}}_{t}$ = $\scriptstyle {\mathbf {\vec {a}}}+{\mathbf {\vec {b}}}$, is then drawn from the start of the first force (the tail) to the end of the second force (the tip).

Grasping this concept is fundamental to understanding how forces interact and combine to influence the motion and equilibrium of objects.

When forces are applied to an extended body (a body that's not a single point), they can be applied at different points. Such forces are called 'bound vectors'. It's important to remember that to add these forces together, they need to be considered at the same point.

The concept of 'net force' comes into play when you look at the total effect of all these forces on the body. However, the net force alone may not necessarily preserve the motion of the body. This is because, besides the net force, the 'torque' or rotational effect associated with these forces also matters. The net force must be applied at the right point, and with the right associated torque, to replicate the effect of the original forces.

When the net force and the appropriate torque are applied at a single point, they together constitute what is known as the resultant force. This resultant force-and-torque combination will have the same effect on the body as all the original forces and their associated torques.

Parallelogram rule for the addition of forces

See also: Parallelogram of force

Parallelogram ABCD