User:Danhoppe/Sandbox
|
Probability density function  | |||
|
Cumulative distribution function 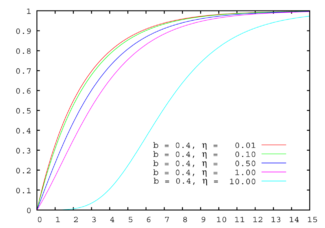 | |||
| Parameters |
scale (real) shape (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean |
where and | ||
| Mode | for , for where | ||
| Variance |
where and | ||
The shifted Gompertz distribution is the distribution of the largest order statistic of two independent random variables which are distributed exponential and Gompertz with parameters b and b and respectively. It has been used as a model of adoption of innovation.
Specification
[edit]Probability density function
[edit]The probability density function of the shifted Gompertz distribution is:
where is the scale parameter and is the shape parameter of the shifted Gompertz distribution.
Cumulative distribution function
[edit]The cumulative distribution function of the shifted Gompertz distribution is:
Properties
[edit]The shifted Gompertz distribution is right-skewed for all values of .
Shapes
[edit]The shifted Gompertz density function can take on different shapes depending on the values of the shape parameter :
- the probability density function has mode 0.
- the probability density function has the mode at where is the smallest root of which is
Related Distributions
[edit]If varies according to a gamma distribution with shape parameter and scale parameter (mean = ), the cumulative distribution function is Gamma/Shifted Gompertz.
See also
[edit]References
[edit]Bemmaor, Albert C. (1994), "Modeling the Diffusion of New Durable Goods: Word-of-Mouth Effect Versus Consumer Heterogeneity", in G. Laurent, G.L. Lilien & B. Pras (ed.), Research Traditions in Marketing, Boston: Kluwer Academic Publishers, pp. 201–223.
Van Den Bulte, Christophe (2004). "Social Contagion and Income Heterogeneity in New Product Diffusion: A Meta-Analytic Test". Marketing Science. 23 (4): 530–544. doi:10.1287/mksc.1040.0054. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Chandrasekaran, Deepa; Tellis, Gerard J. (2007), "A Critical Review of Marketing Research on Diffusion of New Products", in Naresh K. Malhotra (ed.), Review of Marketing Research, vol. 3, Armonk: M.E. Sharpe.




![{\displaystyle be^{-bx}e^{-\eta e^{-bx}}\left[1+\eta \left(1-e^{-bx}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbadea38d6b94a55d5f17ae57cfd323d3087c50d)

![{\displaystyle (-1/b)(\mathrm {E} [\ln(X)]-\ln(\eta ))\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08e2867f3877f7d78ee2f0b15cb788040b5e3d76)

![{\displaystyle {\begin{aligned}\mathrm {E} [\ln(X)]=&[1{+}1/\eta ]\!\!\int _{0}^{\eta }\!\!\!\!e^{-X}[\ln(X)]dX\\&-1/\eta \!\!\int _{0}^{\eta }\!\!\!\!Xe^{-X}[\ln(X)]dX\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e9b1348bed769f35ea2362aa83fc20e11d76102)




![{\displaystyle x^{\star }=[3+\eta -(\eta ^{2}+2\eta +5)^{1/2}]/(2\eta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1676a1bf6ec97c27abcaf11259f46ec7c9d62c7d)
![{\displaystyle (1/b^{2})(\mathrm {E} [\ln(X)^{2}]-(\mathrm {E} [\ln(X)])^{2})\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21b37be46413e129db4f3ee8a0bd2d205d9e868d)
![{\displaystyle {\begin{aligned}\mathrm {E} [\ln(X)^{2}]=&[1{+}1/\eta ]\!\!\int _{0}^{\eta }\!\!\!\!e^{-X}[\ln(X)]^{2}dX\\&-1/\eta \!\!\int _{0}^{\eta }\!\!\!\!Xe^{-X}[\ln(X)]^{2}dX\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/644b50e573de147469ba49bdadafd124f33009d5)

![{\displaystyle f(x;b,\eta )=be^{-bx}e^{-\eta e^{-bx}}\left[1+\eta \left(1-e^{-bx}\right)\right]\mathrm {for} \ x>0\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/727ca6585b1111c6f8221bc7e0ed83dcca6fa4be)






