User:Filip0998

Магнетен Монопол[edit]

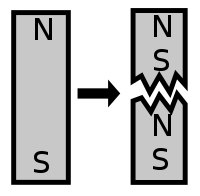
Невозможно е да се направат магнетни монополи од бар-магнет. Ако еден магнет се пресече на половина, не е случај дека една половина има северен пол, а другата половина има јужен пол. Наместо тоа, секое парче има свои северни и јужни полови. Магнетниот монопол не може да се создаде од нормална материја, како што се атомите и електроните, туку би била нова елементарна честичка.

Во Честичната физика , магнетен монопол е хипотетичка елементарна честичка која е изолиран магнет со само еден магнетски пол (северен пол без јужен пол и обратно). Магнетниот монопол ќе има нето "магнетно полнење". Современиот интерес за концептот произлегува од теориите на честички, особено големите унифицирани и суперструјни теории, кои го предвидуваат нивното постоење.

Магнетизмот во бар магнети и електромагнети не е предизвикан од магнетни монополи, и навистина, не постојат познати експериментални или опсервациски докази дека постојат магнетни монополи.

Некои системи со кондензирана материја содржат ефективни (неизолирани) магнетни монополни квази-честички, или содржат феномени кои се математички аналогни на магнетните монополи.

Историско потекло[edit]

Пред дваесеттиот век[edit]

Многу рани научници го припишуваат магнетизмот на лодестоните на две различни "магнетни флуиди" ("effluvia"), течност со северен пол на едниот крај и течност со југ пол на другиот, што привлече и се одбиваше едни со други по аналогија на позитивниот и негативниот електричен набој. Сепак, подобреното разбирање на електромагнетизмот во деветнаесеттиот век покажа дека магнетизмот на ловестоните е правилно објаснет не со магнетни монополни течности, туку со комбинација на електрични струи, електронскиот магнетски момент и магнетните моменти на другите честички. Законот на Гаус за магнетизам, една од Максвеловите равенки, е математичката изјава дека магнетните монополи не постојат. Сепак, Пјер Кири во 1894 година истакна дека може да постојат и магнетни монополи, и покрај тоа што досега не биле видени.

Дваесети век[edit]

Квантната теорија за магнетно полнење започна со хартија од страна на физичарот Пол АМ Дирак во 1931 година. Во овој труд, Дирак покажа дека ако има било какви магнетни монополи во универзумот, тогаш сите електрични набори во универзумот мора да се квантизираат (условот на Дирак-квантизацијата). Електричното полнење е всушност квантизирано, што е во согласност со (но не докажува) постоење на монополи.

Од весникот на Дирак, се направени неколку систематски пребарувања за монополи. Експериментите во 1975 и 1982 година произведоа настани за кандидати кои првично беа толкувани како монополи, но сега се сметаат за неубедливи. Затоа, останува отворено прашањето дали постојат монополи. Понатамошните напредоци во теоријата на физиката на честички, особено случувањата во големите унифицирани теории и квантната гравитација, доведоа до пореални аргументи (детално подолу) кои постојат монополи. Џозеф Полчински, теоретичар на стринг, го опиша постоењето на монополи како "еден од најбезбедните облози што може да ги направи за физиката што сé уште не се видени". Овие теории не се секогаш во согласност со експерименталните докази. Во некои теоретски модели, веројатно нема да се забележат магнетни монополи, бидејќи тие се премногу масивни за да создадат во акцелераторите на честички, а исто така премногу ретки во Универзумот за да влезат во детектор со честички со голема веројатност.

Некои системи за кондензирана материја предлагаат структура површно слична на магнетскиот монопол, познат како цевка на флукс. Краевите на флуксната цевка формираат магнетни диполи, но бидејќи тие се движат независно, тие можат да се третираат за многу цели како независни квазичастици на магнетен монопол. Од 2009 година, голем број новински извештаи од популарните медиуми неправилно ги опишаа овие системи како долгоочекуваното откривање на магнетните монополи, но двата феномени се поврзуваат само еден со друг. Овие системи со кондензирана материја остануваат област на активно истражување.

Полови и магнетизмот во обична материја[edit]

Сите материи кои се изолирани до денес, вклучувајќи го секој атом на периодниот систем и секоја честичка во стандардниот модел, немаат магнетски монополски полнеж. Затоа, обичните феномени на магнетизам и магнети немаат никаква врска со магнетните монополи.

Наместо тоа, магнетизмот во обичната материја доаѓа од два извори. Прво, електричните струи создаваат магнетни полиња според законот на Ампере. Второ, многу елементарни честички имаат вроден магнетски момент, од кои најважен е електронскиот магнетски диполен момент. (Овој магнетизам е поврзан со квантно-механички "спин").

Математички, магнетното поле на објектот често се опишува во смисла на мултиполна експанзија. Ова е израз на полето како збир на полиња на компоненти со специфични математички форми. Првиот термин во експанзијата се нарекува монополски поим, вториот се нарекува диполен, потоа квадрупол, потоа октупол и така натаму. Секој од овие термини може да биде присутен во мултиполното проширување на електричното поле, на пример. Меѓутоа, во мултиполното проширување на магнетното поле, терминот "монопол" е секогаш точно нула (за обична материја). Магнетниот монопол, ако постои, би имал дефинирачко својство за производство на магнетно поле чиј монополски поим е не-нула.

Магнетниот дипол е нешто чие магнетно поле е предоминантно или точно опишано од магнетскиот диполен термин на мултиполната експанзија. Терминот дипол значи два столба, што одговара на фактот дека диполниот магнет обично содржи северен пол од едната страна и јужниот пол од другата страна. Ова е аналогно на електричен дипол, кој има позитивен полнеж од една страна и негативен полнеж од друга страна. Сепак, електричниот дипол и магнетниот дипол се фундаментално сосема различни. Во електричен дипол од обична материја, позитивниот полнеж е изработен од протони, а негативното полнење е направено од електрони, но магнетниот дипол нема различни типови материи создавајќи го северниот пол и јужниот пол. Наместо тоа, двата магнетни столбови се појавуваат истовремено од збирниот ефект на сите струи и внатрешни моменти низ магнетот. Поради ова, двата пола на магнетниот дипол мора секогаш да имаат еднаква и спротивна сила, а двата пола не можат да се одделат едни од други.

Макселови равенки[edit]

Максвеловите равенки на електромагнетизмот ги поврзуваат електричните и магнетните полиња едни со други и со движењата на електричните полнежи. Стандардните равенки обезбедуваат електрични полнежи, но не поставуваат магнетни полнења. Освен за оваа разлика, равенките се симетрични под размена на електрични и магнетни полиња. Всушност, симетричните равенки на Максвел можат да бидат напишани кога сите полнења (а со тоа и електричните струи) се нула, и вака произлегува равенката на електромагнетниот бран.

Целосно симетрични равенките на Максвел, исто така, може да се напишат ако се дозволи можноста за "магнетни полнежи" аналогни на електричните полнежи. Со вклучувањето на променливата за густината на овие магнетни полнења, велат ρm, постои и променлива "густина на магнетна струја" во равенките, jm.

Ако магнетните полнежи не постојат - или ако тие постојат, но не се присутни во простор на вселената - тогаш новите термини во Максвеловите равенки се нула, а проширените равенки се сведуваат на конвенционалните равенки на електромагнетизмот како што е ∇⋅B = 0 (каде што ∇⋅ е дивергенција и B е магнетното поле B).

Лево: Полиња поради стационарни електрични и магнетни монополи.
Десно: Во движење (брзина в), електрично полнење индуцира поле Б додека магнетниот полнеж индуцира поле E. Се користи конвенционална струја.

Горе: E поле поради електричен диполен момент d.
Долно лево: B поле поради математички магнетни дипол m формирана од страна на два магнетни монополи..
Bottom right: B поле поради природен магнетски диполен момент m најден во обична материја (не од магнетни монополи). (Во долниот десен агол не треба да има црвени и сини кругови)

The E полетоs и B полето се должат на електричните полнежи(црно/бело) и магнетен столб (црвено/сино).^[1]^[2]

Во Гаусиан cgs едници[edit]

Проширените равенки на Максвел се следните,во Гаусиан cgs едници:

Максвеловите равенки и равенката на силата на Лоренц со магнетни монополи: единици на Гаусиан cgs
Име	Без магнетни монополи	Со магнетни монополи
Гаусов закон	$\nabla \cdot \mathbf {E} =4\pi \rho _{\mathrm {e} }$
Гаусов закон за магнетизам	$\nabla \cdot \mathbf {B} =0$	$\nabla \cdot \mathbf {B} =4\pi \rho _{\mathrm {m} }$
Фарадеев закон за индукција	$-\nabla \times \mathbf {E} ={\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}$	$-\nabla \times \mathbf {E} ={\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}+{\frac {4\pi }{c}}\mathbf {j} _{\mathrm {m} }$
Амперов закон (со продолжување на Максвел)	$\nabla \times \mathbf {B} ={\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}+{\frac {4\pi }{c}}\mathbf {j} _{\mathrm {e} }$
Лоренцова сила law^[3]^[4]	$\mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +{\frac {\mathbf {v} }{c}}\times \mathbf {B} \right)$	$\mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +{\frac {\mathbf {v} }{c}}\times \mathbf {B} \right)+q_{\mathrm {m} }\left(\mathbf {B} -{\frac {\mathbf {v} }{c}}\times \mathbf {E} \right)$

Во овие равенки ρm е густината на магнетниот полнеж, jm е густината на магнетната струја, а qm е магнетниот полнеж на тест честичка, сите дефинирани аналогно на соодветните количини на електричен полнеж и струја; v е брзината на честичката и c е брзината на светлината. За сите други дефиниции и детали, видете ги Максвеловите равенки. За равенките во недимензионална форма, отстранете ги факторите на c.

Во SI едници[edit]

Во единиците на SI, постојат две спротивставени единици кои се користат за магнетно полнење qm: мрежи (Wb) и ампериметри (Аm). Конверзијата помеѓу нив е qm (Wb) = μ0qm (A · m), бидејќи единиците се 1 Wb = 1 H · A = (1 H · m-1) · (1 A · m) со димензионална анализа (H е Хенри - SI единица на индуктивност).

Максвеловите равенки потоа ги земаат следните форми (користејќи ја истата нотација погоре):

Максвеловите равенки и равенката на силата на Лоренц со магнетни монополи: SI единици
Име	Без магнетни монополи	Со магнетни монополи
Име	Без магнетни монополи	Вебер конвенција	Ампер-метарска конвенција
Гаусовиот закон	$\nabla \cdot \mathbf {E} ={\frac {\rho _{\mathrm {e} }}{\varepsilon _{0}}}$
Гаусовиот закон за магнетизам	$\nabla \cdot \mathbf {B} =0$	$\nabla \cdot \mathbf {B} =\rho _{\mathrm {m} }$	$\nabla \cdot \mathbf {B} =\mu _{0}\rho _{\mathrm {m} }$
Фарадеев закон за индукција	$-\nabla \times \mathbf {E} ={\frac {\partial \mathbf {B} }{\partial t}}$	$-\nabla \times \mathbf {E} ={\frac {\partial \mathbf {B} }{\partial t}}+\mathbf {j} _{\mathrm {m} }$	$-\nabla \times \mathbf {E} ={\frac {\partial \mathbf {B} }{\partial t}}+\mu _{0}\mathbf {j} _{\mathrm {m} }$
Амперов закон (со проширување на Максвел)	$\nabla \times \mathbf {B} ={\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}+\mu _{0}\mathbf {j} _{\mathrm {e} }$
Лоренцова сила на равенката	$\mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)$	${\begin{aligned}\mathbf {F} ={}&q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)+\\&{\frac {q_{\mathrm {m} }}{\mu _{0}}}\left(\mathbf {B} -\mathbf {v} \times {\frac {\mathbf {E} }{c^{2}}}\right)\end{aligned}}$	${\begin{aligned}\mathbf {F} ={}&q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)+\\&q_{\mathrm {m} }\left(\mathbf {B} -\mathbf {v} \times {\frac {\mathbf {E} }{c^{2}}}\right)\end{aligned}}$

Тензорска формулација[edit]

Максвеловите равенки на јазикот на тензор ја прави Лоренц коваријансата јасна.Генерализираните равенки се:

Максвел равенки	Гаусови единици	SI единици (Wb)	SI единици (A⋅m)
Фарадеј-Гаус закон	$\partial _{\alpha }F^{\alpha \beta }={\frac {4\pi }{c}}J_{\mathrm {e} }^{\beta }$	$\partial _{\alpha }F^{\alpha \beta }=\mu _{0}J_{\mathrm {e} }^{\beta }$	$\partial _{\alpha }F^{\alpha \beta }=\mu _{0}J_{\mathrm {e} }^{\beta }$
Ампер-Гаус закон	$\partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {4\pi }{c}}J_{\mathrm {m} }^{\beta }$	$\partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {1}{c}}J_{\mathrm {m} }^{\beta }$	$\partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {\mu _{0}}{c}}J_{\mathrm {m} }^{\beta }$
Лоренц сила закон	${\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+q_{\mathrm {m} }{{\tilde {F}}_{\alpha \beta }}\right]{\frac {v^{\beta }}{c}}$	${\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{\mu _{0}c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }$	${\frac {dp_{\alpha }}{d\tau }}=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }$

каде

$F αβ$ е електромагнетски тензор, $~Fαβ = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}1/2εαβγδFγδ$ е двојниот електромагнетски тензор,
за честичка со електричен полнеж $q e$ и магнетен полнеж $q m$ ; $v$ е четири брзина и $p$ четири импулси,
за електрична и магнетна дистрибуција на полнеж; $J e = (ρ e, j e)$ е електричен четири струи и $J m = (ρ m, j m)$ магнетна четири-струја.

За честичка која има само електричен полнеж, може да се изрази своето поле со помош на четири потенцијали, според стандардната ковариантна формулација на класичниот електромагнетизам:

F_{\alpha \beta }=\partial _{\alpha }A_{\beta }-\partial _{\beta }A_{\alpha }\,

Сепак, оваа формула е несоодветна за честичка која има и електричен и магнетски полнеж, и ние мора да додадеме термин кој вклучува друг потенцијален P.

F_{\alpha \beta }=\partial _{\alpha }A_{\beta }-\partial _{\beta }A_{\alpha }\ +\partial ^{\mu }(\varepsilon _{\alpha \beta \mu \nu }P^{\nu }),

Оваа формула за полињата често се нарекува Кабиббо-Ферари, иако Шанмугадасан го предложи тоа порано. Количината εαβγδ е симбол на Леви-Чивита, а индексите (како и обично) се однесуваат според конвенцијата за збир на Ајнштајн.

Двојна трансформација[edit]

Генерализираните равенки на Максвел имаат одредена симетрија, наречена трансформација на двојност. Може да се избере било кој вистински агол ξ, а истовремено да се променат полињата и обвиненијата насекаде во универзумот како што следи (во Gaussian единици):

Надоместоци и струи	Полиња
${\begin{pmatrix}\rho _{\mathrm {e} }\\\rho _{\mathrm {m} }\end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\rho _{\mathrm {e} }'\\\rho _{\mathrm {m} }'\end{pmatrix}}$	${\begin{pmatrix}\mathbf {E} \\\mathbf {H} \end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {E'} \\\mathbf {H'} \end{pmatrix}}$
${\begin{pmatrix}\mathbf {J} _{\mathrm {e} }\\\mathbf {J} _{\mathrm {m} }\end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {J} _{\mathrm {e} }'\\\mathbf {J} _{\mathrm {m} }'\end{pmatrix}}$	${\begin{pmatrix}\mathbf {D} \\\mathbf {B} \end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {D'} \\\mathbf {B'} \end{pmatrix}}$

каде што основните количини се полнежите и полињата пред трансформацијата, а непостоените количини се после трансформацијата. Полињата и полнежите по оваа трансформација се уште ги почитуваат истите Максвелова равенки. Матрицата е дводимензионална ротациона матрица.

Поради трансформацијата на двојноста, не може еднозначно да се одлучи дали честичка има електричен полнеж, магнетно полнење, или и двете, само со набљудување на неговото однесување и споредување на тоа со Максвеловите равенки. На пример, тоа е само конвенција, а не барање на Максвеловите равенки, дека електроните имаат електричен полнеж, но не и магнетно полнење; по трансформацијата ξ = π / 2, тоа би било обратно. Клучниот емпириски факт е дека сите забележани честички имаат ист сооднос на магнетно полнење со електричен полнеж.Двојните трансформации може да го променат односот на било која произволна нумеричка вредност, но не може да го промени фактот дека сите честички имаат ист сооднос. Бидејќи ова е случај, може да се направи трансформација на двојност која го поставува овој сооднос на нула, така што сите честички немаат магнетно полнење. Овој избор е во основата на "конвенционалните" дефиниции за електрична енергија и магнетизам.

Квантизацијата на Дирак[edit]

Еден од дефинираните напредоци во квантната теорија беше работата на Пол Дирак за развој на релативистички квантен електромагнетизам. Пред неговата формулација, присуството на електричен полнеж беше едноставно "вметнато" во равенките на квантната механика (QM), но во 1931 Дирак покажа дека дискретно полнење природно "паѓа" од QM. Тоа е да се каже, ние можеме да ја одржиме формата на Максвеловите равенки и се уште има магнетни полнежи.

Размислете за систем кој се состои од еден стационарен електричен монопол (еден електрон, да речеме) и еден стационарен магнетски монопол. Класично, електромагнетното поле што ги опкружува има густина на импулсот дадена од векторот Појнтинг, а исто така има и вкупен аголен импулс, кој е пропорционален на производот qeqm и независен од растојанието меѓу нив.

Квантната механика диктира, сепак, дека аголниот моментум е квантизиран во единиците на ħ, па затоа производот qeqm, исто така, мора да се квантизира. Ова значи дека ако во универзумот постои и единствен магнетски монопол, а формата на Максвеловите равенки е валидна, тогаш сите електрични полнежи ќе се квантизираат.

Кои се единиците во кои ќе се квантифицира магнетното полнење? Иако би било можно едноставно да се интегрира низ целиот простор за да се најде вкупниот аголен импулс во горенаведениот пример, Дирак презеде поинаков пристап. Ова го доведе до нови идеи. Тој сметаше магнетно полнење слично на точка чие магнетно поле се однесува како qm / r 2 и е насочено во радијална насока, лоцирано во потеклото. Бидејќи дивергенцијата на Б е еднаква на нула речиси насекаде, освен за локусот на магнетниот монопол во r = 0, може локално да се дефинира векторскиот потенцијал така што кривината на векторскиот потенцијал А е еднаква на магнетното поле B.

Сепак, векторскиот потенцијал не може да се дефинира глобално токму поради тоа што дивергенцијата на магнетното поле е пропорционална со делтата функцијата на Дирак во потеклото. Мораме да дефинираме еден сет на функции за векторскиот потенцијал на "северната хемисфера" (полустената z> 0 над честичката) и друг сет на функции за "јужната хемисфера". Овие два векторни потенцијали се совпаѓаат на "екваторот" (рамнината z = 0 преку честичката), и тие се разликуваат со мерач трансформација. Функцијата на брановите на електрично наелектризирана честичка ("сонда") што орбитира околу "екваторот" генерално се менува со фаза, слично како во ефектот Ахаронов-Бохм. Оваа фаза е пропорционална на електричниот полнеж qe на сондата, како и на магнетното полнење qm на изворот. Дирак првично го разгледувал електронот чија функција на бранови е опишана со дираковската равенка.

Бидејќи електронот се враќа во истата точка по целото патување околу екваторот, фазата φ на неговата бранова функција eiφ мора да биде непроменета, што значи дека фазата φ додадена на брановата функција мора да биде повеќекратна од 2π:

Единици	Состојба
Гаусовски единици на ЦГС	$2{\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{\hbar c}}\in \mathbb {Z}$
SI единици (вебер конвенција)^[5]	${\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{2\pi \hbar }}\in \mathbb {Z}$
SI единици (Амперова·метарски конвенција)	${\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{2\pi \varepsilon _{0}\hbar c^{2}}}\in \mathbb {Z}$

каде што ε0 е вакуумната диелектричност, ħ = h / 2π е намалена константа на Планк, c е брзината на светлината, и ℤ е множество на цели броеви.

Ова е познато како услов за квантификација на Дирак. Хипотетичкото постоење на магнетна монопола би значело дека електричниот полнеж мора да се квантизира во одредени единици; исто така, постоењето на електрични полнежи подразбира дека магнетните обвиненија на хипотетичките магнетни монополи, доколку постојат, мора да се квантизираат во единици обратно пропорционални со основното електрично полнење.

Во тоа време не беше јасно дали постои такво нешто, па дури и требаше. Впрочем, може да дојде до друга теорија која би ја објаснила квантизацијата на полнежите без потреба од монополи. Концептот остана нешто од љубопитност. Меѓутоа, во времето по објавувањето на оваа плодна работа, не се појави друго широко прифатено објаснување за квантизацијата на полнежот. (Концептот на локална калибрација на инвариантност - види теорија на калибар - обезбедува природно објаснување за квантизацијата на полнеж, без да се повика на потребата за магнетни монополи, но само ако групата на U (1) е компактна, во кој случај ние во секој случај имаме магнетни монополи. )

Ако максимално ја прошириме дефиницијата на векторскиот потенцијал за јужната хемисфера, таа се дефинира насекаде, освен полу-бесконечна линија која се протега од потеклото во правец кон северниот пол. Оваа полу-бесконечна линија се нарекува низа на Дирак и нејзиното дејство врз функцијата на брановите е аналогно на ефектот на соленоид во ефектот Ахаронов-Бохм. Состојбата на квантификација произлегува од барањето дека фазите околу Дирацката низа се тривијални, што значи дека низата на Дирак мора да биде нефизичка. Стригата на Дирак е само артефакт на коригираната табела што се користи и не треба да се сфати сериозно.

Дираковиот монополот е единствен раствор на Максвеловата равенка (затоа што бара отстранување на светлината од spacetime); во покомплицирани теории, тој е заменет со мазно решение, како што е монополот "t hooft-polyakov".

Тополошка интерпретација[edit]

Дирак стринг[edit]

Теоријата за мерење, како што е електромагнетизмот, се дефинира со поле за мерење кое го поврзува групниот елемент со секој пат во просторот. За бесконечно мали патеки, елементот на групата е близу до идентитетот, додека за подолги патеки елементот на групата е сукцесивен производ на бесконечно мала група елементи на патот.

Во електродинамиката, групата е U (1), единица комплексни броеви под множење. За бесконечно мали патеки, елементот на групата е 1 + iAμdxμ што имплицира дека за конечни патеки параметрирани од s, групата е:

\prod _{s}\left(1+ieA_{\mu }{dx^{\mu } \over ds}\,ds\right)=\exp \left(ie\int A\cdot dx\right).

Мапата од патеките до елементите на групата се нарекува Вилсоновска јамка или холономија, а за U (1) мерен група е фазниот фактор кој што волффункцијата на наелектризирана честичка се стекнува додека ја поминува патеката.За јамка:

e\oint _{\partial D}A\cdot dx=e\int _{D}(\nabla \times A)\,dS=e\int _{D}B\,dS.

Така што фазата на наелектризирана честичка добива кога се движи во јамка е магнетниот флукс низ јамката. Кога мала соленоида има магнетен флукс, постојат пречки за препреки за наелектризирани честички кои се движат околу соленоид или околу различни страни на соленоид, кои го откриваат неговото присуство.

Но, ако сите полнежи за честички се целобројни множители на e, соленоидите со флукс од 2π / e немаат пречки на интерференција, бидејќи фазниот фактор за која било наелектризирана честичка е e2πi = 1. Таквиот соленоид, ако е тенок доволно, е квантно механички невидлив.Ако таков соленоид требаше да носи проток од 2π / e, кога флуксот протекува од еден од неговите краеви, тој не би се разликувал од монополот.

Монополното решение на Дирак всушност опишува бесконечно мала соленоидна линија која завршува во точка, а локацијата на соленоид е еднина дел од растворот, низата на Дирак. Структури на Дирак ги поврзуваат монополите и антимонополите со спротивен магнетски полнеж, иако во верзијата на Дирак, стрингот едноставно оди до бесконечност. Стрингот е невнимателен, така што можете да го ставите насекаде, и со користење на два координатни закрпи, полето во секој лепенка може да се направи несуштински со лизгање на низата до онаа каде што не може да се види.

Големи унифицирани теории[edit]

Во U (1) мерач група со квантизирани задолжен, групата е круг со радиус 2π / e. Таква U (1) мерен група се нарекува компактна. Секоја U (1) која доаѓа од голема унифицирана теорија е компактна - бидејќи само компактните групи со повисоки мерачи имаат смисла. Големината на групата на мерачи е мерка на константната константа за спојување, така што во границите на група со голем волумен, интеракцијата на секоја фиксна репрезентација оди на нула.

Случајот со групата на U (1) е посебен случај, бидејќи сите негови непривлечни претстави се со иста големина - наборот е поголем од цел број, но полето е сè уште само комплексен број - така што во U (1 ) Математичка теорија на полето е можно да се преземе декомпактифицираната граница без контрадикција. Квантот на полнежот станува мал, но секоја наелектризирана честичка има огромен број полнења за полнење, така што нејзиното полнење останува ограничено. Во некомпактна U (1) теорија на групата на мерачи,полнежите на честичките се генерички нечии кратки единици. Бидејќи квантизацијата на полнеж е експериментална сигурност, јасно е дека U (1) мерен група на електромагнетизам е компактна.

GUTs доведуваат до компактни U (1) мерачи, така што ја објаснуваат квантизацијата на полнеж на начин кој изгледа логично независен од магнетните монополи. Сепак, објаснувањето е во суштина истото, бидејќи во секој GUT кој се распаѓа во U (1) мерач на долги растојанија, постојат магнетни монополи.

Аргументот е тополошки:

Холономијата на полето за мерење ги прикажува јамките до елементите на мерачот. Инфинитимални јамки се мапирани во групите бесконечно близу до идентитетот.
Ако замислите голема сфера во вселената, можете да деформирате бесконечно мала јамка која започнува и завршува на северниот пол како што следува: истегнете ја јамката преку западната хемисфера додека не стане голем круг (кој сè уште започнува и завршува на северниот пол ) тогаш нека се смали назад кон мала јамка додека одите преку источната хемисфера. Ова се нарекува ласење на сферата.
Ласење е секвенца на јамки, така што холономијата го прикажува во секвенца на групни елементи, континуирана патека во групата на мерачи. Бидејќи јамката на почетокот на ласењето е иста како и јамката на крајот, патеката во групата е затворена.
Ако групната патека поврзана со процедурата на ласење се врти околу U (1), сферата содржи магнетно полнење. За време на ласењето, холономијата се менува од количината на магнетниот тек низ сферата.
Бидејќи холономијата на почетокот и на крајот е идентитетот, вкупниот магнетски флукс е квантизиран. Магнетниот полнеж е пропорционален на бројот на намотки N, магнетниот флукс низ сферата е еднаков на 2πN / e. Ова е состојбата на Дирак-квантизацијата, и тоа е тополошка состојба која бара конфигурации на долги растојанија од U (1) на полето да бидат конзистентни.
Кога U (1) мерачот група доаѓа од кршење на компактна Лие група, патот што врти околу U (1) група доволно пати е тополошки тривијална во големата група. Во не-U (1) компактна група Лие, покривниот простор е група Лие со истата Лиева алгебра, но каде што сите затворени јамки се склони. Групите на Ли се хомогени, така што секој циклус во групата може да се помести, така што тој започнува со идентитетот, тогаш неговото лифт до покривната група завршува на P, што претставува лифт од идентитетот. Одење околу јамката двапати ќе ве однесе до P2, три пати на P3, сите лифтови на идентитетот. Но, постојат само многу многу лифтови на идентитетот, бидејќи лифтовите не можат да се акумулираат. Овој број на пати што треба да се помине низ јамката за да се направи склучен е мал, на пример, ако GUT групата е SO (3), групата за покривање е SU (2), и одење околу секоја јамка двапати е доволно. ()!!!
Ова значи дека постои постојана конфигурација на мерен-поле во групата ГУТ овозможува U (1) монополната конфигурација да се одмора на кратки растојанија, по цена на не останувајќи во U (1). За да го направите ова со што е можно помалку енергија, треба да ја оставите само групата на U (1) во близина на една точка, која се нарекува јадро на монополата. Надвор од јадрото, монополот има само енергија од магнетно поле.

Оттука, Дирак монополот е тополошки дефект во компактната U (1) мерач теорија. Кога нема GUT, дефектот е сингуларност - јадрото се собира кон точка. Но, кога има некаков регулатор на кратко растојание во просторот, монополите имаат конечна маса. Монополи се случуваат во решетката U (1), и таму јадрото е големината на решетката. Генерално, се очекува да се појават секогаш кога постои регулатор на краток растојание.

Теорија на низа[edit]

Во универзумот, квантната гравитација обезбедува регулатор. Кога гравитацијата е вклучена, монополната сингуларност може да биде црна дупка, а за големи магнетни набори и маса, масата на црна дупка е еднаква на полнењето на црна дупка, така што масата на магнетната црна дупка не е бесконечна. Ако црна дупка целосно може да се распадне со радијација со Хокинг, најсветлата наелектризирана честичка не може да биде премногу тешка. Најлесниот монопол треба да има маса помала или споредлива со нејзиното полнење во природните единици.

Значи, во конзистентна холографска теорија, за која теоријата на низи е единствениот познат пример, секогаш постојат монополи со конечни маси. За обичниот електромагнетизам, горната граница на маса не е многу корисна, бидејќи е за иста големина како и масата на Планк.

Математичка формулација[edit]

Во математиката, полето (класично) мерач е дефинирано како врска над главен G-bundle над просторот. G е мерач група, и таа дејствува на секое влакно од пакетот посебно.

Поврзувањето на G-bundle ви кажува како да ги лепиме влакната заедно во блиските точки на M. Таа започнува со континуирана група на симетрија G која делува на влакно F, а потоа го поврзува групата со секој бесконечно мал пат. Множењето на групата по која било патека ви кажува како да се движите од една точка на пакетот на друг, со тоа што елементот Г е поврзан со патот чин на фибер Ф.

Во математиката, дефиницијата на пакетот е дизајнирана да ја нагласи топологијата, така што идејата за поврзување е додадена како последователна. Во физиката, врската е основниот физички објект. Едно од фундаменталните набљудувања во теоријата на карактеристичните класи во алгебарската топологија е дека многу хомотопски структури на нетривиалните главни снопови можат да се изразат како интеграл на некој полином над било каква врска над неа. Забележете дека поврзувањето преку тривијален пакет не може да ни даде нетривијален главен пакет.

Ако времето-просторот е ℝ4, се поврзува просторот од сите можни врски на G-пакетот. Но, размислете што се случува кога ќе се отстрани временската линија од време-просторот. Резултираното времетраење на времето е хомотетички еквивалентно на тополошката сфера S2.

Главен G-bundle над S2 се дефинира со покривање на S2 со две графикони, секоја од нив домамоморфни на отворената 2-топка така што нивната пресек е хомеоморфна на лентата S1 × I. 2-топки се хомотопски тривијални и лентата е хомотепски еквивалентна на кругот S1. Значи, тополошката класификација на можните врски се сведува на класификација на транзиционите функции. Функцијата за транзиција ја мапира лентата до G, а различните начини на мапирање лента во G се дадени од првата хомотопија група од G.

Така, во формулацијата на G-bundle, теоријата на мерачот признава монополи на Дирак ако G не е едноставно поврзан, секогаш кога постојат патеки што одат околу групата која не може да се деформира на константен пат (патека чија слика се состои од една точка). U (1), кој има квантизирани полнежи, не е едноставно поврзан и може да има монополи на Дирак, додека ℝ, нејзината универзална покривна група е едноставно поврзана, нема квантифицирани полнежи и не ги прифаќа монополите на Дирак. Математичката дефиниција е еквивалентна на дефиницијата за физика, под услов да се дозволуваат следниве полиња на Дирак-мера, кои се дефинирани само за далноводи, а полето на мерачот на различни лепенки е залепено по мерење на трансформација.

Вкупниот магнетски тек е никој друг освен од првиот број на Черн на главниот пакет и зависи само од изборот на главниот пакет, а не специфичната поврзаност над неа. Со други зборови, тоа е тополошки инвариант.

Овој аргумент за монополи е повторливост на аргументот за ласо за чиста U (1) теорија. Тој се генерализира на d + 1 димензии со d ≥ 2 на неколку начини. Еден начин е да се прошири сè во дополнителните димензии, така што U (1) монополи стануваат листови со димензија d-3. Друг начин е да се испита типот на тополошката сингуларност во точка со хомотопијална група πd-2 (G).

Големи унифицирани теории[edit]

Во поново време, нова класа на теории, исто така, сугерира постоење на магнетни монополи.

Во текот на раните 1970-ти, успесите на квантната теорија на полето и теоријата на мерење во развојот на електрослаба теорија и математиката на силната нуклеарна сила доведоа до тоа многу теоретичари да се обидат да ги комбинираат во една единствена теорија позната како Голема унифицирана теорија ( GUT). Предложени се неколку GUTs, од кои повеќето укажуваа на присуство на вистинска магнетна монополска честичка. Попрецизно, GUTs предвиделе голем број честички познати како диони, од кои најосновната состојба била монопола. Полнежот на магнетните монополи предвидени со GUTs е или 1 или 2 gD, во зависност од теоријата.

Поголемиот дел од честичките што се појавуваат во било која квантна теорија на полето се нестабилни и се распаѓаат во други честички во различни реакции кои мора да ги задоволуваат различните закони за зачувување. Стабилните честички се стабилни, бидејќи нема полесни честички во кои тие можат да се распаѓаат и се уште ги задоволуваат законите за конзервација. На пример, електронот има број на лептон од еден и електричен полнеж од еден, и немаат полесни честички кои ги зачувуваат овие вредности. Од друга страна, мионот, во суштина тежок електрон, може да се распаѓа во електрони плус два кванти на енергија, и оттаму не е стабилен.

Дионите во овие GUTs се исто така стабилни, но со сосема друга причина. Дионите се очекува да постојат како пропратен ефект на "замрзнување" на условите на раниот универзум, или кршење на симетријата. Во ова сценарио, дионите се јавуваат поради конфигурацијата на вакуумот во одредена област на универзумот, според оригиналната теорија на Дирак. Тие остануваат стабилни не поради состојбата на конзервација, туку затоа што не постои поедноставна тополошка состојба во која тие можат да се распаѓаат.

Должината на која постои оваа специјална вакуумска конфигурација се нарекува корелациона должина на системот. Должината на корелација не може да биде поголема од причината што би овозможила, па затоа корелационата должина за изработка на магнетни монополи мора да биде барем толку голема колку големина на хоризонтот одредена од метриката на проширувањето на универзумот. Според таа логика, треба да има барем еден магнетски монопол по обем на хоризонтот, како што беше кога се случило кршењето на симетријата.

Космолошките модели на настаните кои следат по големиот тресок прават предвидувања за тоа каков е обемот на хоризонтот, што доведува до предвидувања за моменталната густина на монополи. Раните модели предвидуваат огромна густина на монополи, во јасна контрадикција со експерименталните докази.Ова беше наречено "монополски проблем". Нејзината широко прифатена резолуција не беше промена во предвидување на монополи во физиката на честички, туку во космолошките модели кои се користат за да се заклучи нивната моментална густина. Поконкретно, поновите теории за космичка инфлација драстично го намалуваат предвидениот број на магнетни монополи, до густина доволно мала за да биде изненадувачка што луѓето никогаш не ја виделе.Оваа резолуција на "монополскиот проблем" се сметаше за успех на теоријата на космичка инфлација. (Сепак, се разбира, тоа е само значаен успех ако предвидување на монополи во физиката е точен). Од овие причини, монополи станаа главен интерес во 1970-тите и 80-тите години, заедно со другите "пристапни" предвидувања GUTs како протон распаѓање.

Многу од другите честички предвидени од овие GUTs беа надвор од способностите на тековните експерименти за откривање. На пример, широка класа на честички познати како X и Y бозони се предвидени да посредуваат во спојувањето на електрпслабите и силните сили, но овие честички се екстремно тешки и многу повеќе од можностите на било кој разумен забрзувач на честички за да се создаде.

Пребарувања за магнетни монополи[edit]

Експериментални пребарувања за магнетни монополи може да се стават во една од две категории: оние кои се обидуваат да ги детектираат постоечките магнетни монополи и оние кои се обидуваат да создадат и да детектираат нови магнетни монополи.

^ Parker, C. B. (1994). McGraw-Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. ISBN 0-07-051400-3.
^ Mansfield, M.; O'Sullivan, C. (2011). Understanding Physics (4th ed.). John Wiley & Sons. ISBN 978-0-47-0746370.
^ Cite error: The named reference moulin-2001 was invoked but never defined (see the help page).
^ Rindler, Wolfgang (November 1989). "Relativity and electromagnetism: The force on a magnetic monopole". American Journal of Physics. 57 (11). American Journal of Physics: 993–994. Bibcode:1989AmJPh..57..993R. doi:10.1119/1.15782.
^ Jackson 1999, section 6.11, equation (6.153), page 275

[1] Parker, C. B. (1994). McGraw-Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. ISBN 0-07-051400-3.

[2] Mansfield, M.; O'Sullivan, C. (2011). Understanding Physics (4th ed.). John Wiley & Sons. ISBN 978-0-47-0746370.

[moulin-2001-3] Cite error: The named reference moulin-2001 was invoked but never defined (see the help page).

[4] Rindler, Wolfgang (November 1989). "Relativity and electromagnetism: The force on a magnetic monopole". American Journal of Physics. 57 (11). American Journal of Physics: 993–994. Bibcode:1989AmJPh..57..993R. doi:10.1119/1.15782.

[5] Jackson 1999, section 6.11, equation (6.153), page 275

[1]

[2]

[3]

[4]

[5]