User:Gommini

초전도체의 기본적인 성질

초전도체의 비열이나 초전도성이 깨질 때의 임계 온도, 임계 자기장, 임계 전류 밀도와 같은 대부분의 성질은 물질마다 다르다.

그러나 한편으로는, 물질이 무엇이냐에 상관없이 초전도체이면 공통적으로 가지는 성질들이 있다. 예를 들면 모든 초전도체는 자기장이 없을 때 작은 전류에 대해 정확히 0인 전기 저항을 가진다. 이러한 '공통적인' 성질은 초전도성이 하나의 열역학적인 상이며, 물질의 미시적인 구조에 독립적인 특정한 성질을 가진다는 것을 암시한다.

DC에서의 초전도

시료의 전기적인 저항을 측정하는 가장 간단한 방법은 그 물질을 전기 회로에서 전류원과 직렬로 연결한 뒤 전류 I를 공급하고 시료 양단에 인가되는 전압 V를 측정하는 것이다. 시료의 저항은 옴의 법칙에 따라 $R={\frac {V}{I}}$ 로 주어진다. 만약 전압이 0이라면, 이것은 저항이 0임을 의미하며 그 시료는 초전도 상태에 있는 것이다.

또한 초전도는 전압이 인가되지 않은 상태에서도 전류를 유지할 수 있다. 이런 성질은 MRI와 같이 초전도 전자석을 이용하는 곳에서 사용된다. 실험에 의하면 초전도 코일은 측정 가능한 감소 없이 전류를 몇 년씩 유지할 수 있는 것으로 나타났다. 실험에 의하면 이런 전류의 유효수명은 최소한 100,000년이며, 이론적으로는 우주의 수명보다도 길 것으로 평가된다.

일반적인 도체에서는, 전류는 전자가 무거운 이온 격자 사이를 움직여 가는 것으로 표현된다. 전자들은 이온과 격자에 계속 충돌하며, 각각의 추돌에서 전류에 의해 전달되던 에너지의 일부가 격자로 흡수되고 열로 변환된다. 이것이 이온 격자의 운동에너지이다. 결과적으로 전류에 의해 운반되던 에너지는 점점 흩어진다. 이것이 전기적 저항이 일어나는 현상이다.

초전도체에서는 상황이 다르다. 일반적인 초전도체에서 전류의 흐름은 각각의 전자의 움직임으로 분리될 수 없다. 그 대신 전자는 Cooper 쌍이라는 쌍으로 묶인다. 포논의 교환에 의한 전자들 사이의 인력으로 생긴다. 양자 역학에 의해, 이러한 Cooper 쌍의 흐름은 에너지 스펙트럼에서 에너지 갭을 만들어내는데, 이는 전자의 흐름을 흥분시키기 위해서는 최소한 ΔE만큼의 에너지가 필요함을 의미한다. 그러므로, 만약 ΔE가 kT로 주어지는 격자의 열 에너지보다 크다면 (k는 볼츠만 상수이고 T는 온도이다.), 전자는 격자에 의해 산란되지 않게 된다. 그러므로 Cooper 쌍은 초유체를 이루며, 이는 에너지 손실없이 흐를 수 있다는 것을 의미한다.

모든 종류의 고온 초전도체를 포함하는 2종 초전도체는 초전도 상전이의 근방에서 전류가 그 전류로 인해 발생할 수도 있는 강한 자기장과 함께 가해졌을 때 아주 작은 양의 비저항을 보인다. 이것은 전자 초유체의 vortex(와동)에 의한 것으로서, 전류에 의해 전달되는 에너지의 일부를 흩뜨린다. 만약 전류가 충분히 작다면, vortex는 정지해있고 비저항은 사라진다. 이 효과에 의한 저항은 초전도체가 아닌 물질이 보이는 저항에 비하면 아주 작지만, 민감한 실험을 할 때에는 고려해야 한다. 그러나, 온도가 초전도 상전이에서 더 멀어짐에 따라, 이러한 vortex들은 불규칙하지만 고정되어 있는 "vortex glass"라는 상으로 변할 수 있다. 이러한 "vertex glass" 상전이 온도 아래에서는 초전도체의 저항이 정말로 0이 된다.

초전도 상전이

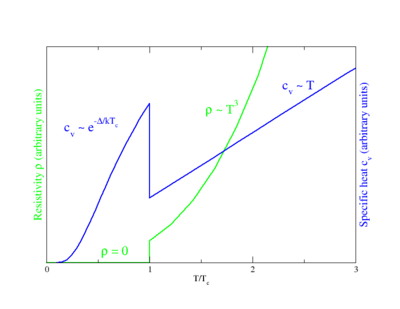
초전도 상태는 물질의 온도가 초전도 상전이가 일어나는 임계 온도 T_c이하로 내려갈 때 나타난다. 임계 온도의 값은 물질에 따라 다르다. (고온 초전도체가 아닌) 일반 초전도체들은 보통 20 K(kelvin)에서 1K 이하까지의 값을 가진다. 예를 들어 고체수은은 4.2 K의 임계 온도를 가진다. 현재까지 발견된 (고온 초전도체가 아닌) 일반 초전도체들의 임계온도는 2001년에 발견된 [[MgB₂]]에서 보이는 39 K이 최고이다. (단 이 물질이 보여준 성질 때문에 MgB₂를 일반 초전도체로 분류할 것이냐에 대해서는 논란이 있다.) 구리계 초전도체는 훨씬 높은 임계 온도를 가지는데, 최초로 발견된 구리계 초전도체 중의 하나인 YBa₂Cu₃O₇의 임계 온도는 92 K이며, 수은을 포함한 구리계 초전도체는 임계온도가 130 K을 넘는 것도 있다. 이런 높은 임계 온도에 대한 확실한 이론적 설명은 알려져 있지 않다. 일반 초전도체는 포논(phonon)의 교환에 의한 전자 쌍의 형성으로 설명되지만, 최근 발견된 고온 초전도체에 대해서는 이 설명이 맞지 않는다.

초전도성이 나타날 때는 다양한 물리량의 갑작스런 변화가 수반되는데, 이것은 상전이(phase transition)의 특징이다. 예를 들어, 전자에 의한 비열은 일반적으로 온도에 1승에 비례한다. 그러나 초전도 상전이를 할 때에 비열값은 갑자기 뛰어오르고 그 이후로는 더 이상 1승에 비례하지 않고 e^{−α /T}에 비례하게 된다. (α는 물질에 따라 정해지는 상수) 이런 양상은 에너지 갭의 존재에 대한 증거이다.

초전도 상전이의 상전이 차수는 논란의 대상이다. 실험 결과로 보면 초전도 상전이들은 잠열이 없는 2차 상전이인 것으로 보인다. 그러나 1970년 대의 계산에 의하면 초전도 상전이는 1차 상전이인데 전자기장의 장거리 요동에 의한 효과 때문에 약하게 보이는 것일 수도 있다. 최근에서야 무질서 장 이론(Disorder Field Theory)의 도움으로 vortex line이 초전도성에 중요한 역할을 하며, 초전도 상전이는 type I 영역에서는 1차이고 type II 영역에서는 2차이며 두 영역은 삼중점에 의해 분리됨이 보여진 바 있다.

마이스너 효과

외부의 자기장 H이 초전도체에 가해지면 얇은 두께 λ(London 투과 깊이(London penetration depth))만큼만 투과할 수 있다. 그보다 더 깊은 곳에서는 자기장이 급격히 감소하여 사라진다. 이것을 마이스너 효과(Meissner effect)라 하며, 초전도체를 규정짓는 중요한 특성이다. 대부분의 초전도체에서 이 깊이는 100nm 수준이다.

The Meissner effect is sometimes confused with the kind of diamagnetism one would expect in a perfect electrical conductor: according to Lenz's law, when a changing magnetic field is applied to a conductor, it will induce an electrical current in the conductor that creates an opposing magnetic field. In a perfect conductor, an arbitrarily large current can be induced, and the resulting magnetic field exactly cancels the applied field.

The Meissner effect is distinct from this because a superconductor expels all magnetic fields, not just those that are changing. Suppose we have a material in its normal state, containing a constant internal magnetic field. When the material is cooled below the critical temperature, we would observe the abrupt expulsion of the internal magnetic field, which we would not expect based on Lenz's law.

The Meissner effect was explained by the brothers Fritz and Heinz London, who showed that the electromagnetic free energy in a superconductor is minimized provided

\nabla ^{2}\mathbf {H} =\lambda ^{-2}\mathbf {H} \,

where H is the magnetic field and λ is the London penetration depth.

This equation, which is known as the London equation, predicts that the magnetic field in a superconductor decays exponentially from whatever value it possesses at the surface.

The Meissner effect breaks down when the applied magnetic field is too large. Superconductors can be divided into two classes according to how this breakdown occurs. In Type I superconductors, superconductivity is abruptly destroyed when the strength of the applied field rises above a critical value H_c. Depending on the geometry of the sample, one may obtain an intermediate state consisting of regions of normal material carrying a magnetic field mixed with regions of superconducting material containing no field. In Type II superconductors, raising the applied field past a critical value H_c1 leads to a mixed state in which an increasing amount of magnetic flux penetrates the material, but there remains no resistance to the flow of electrical current as long as the current is not too large. At a second critical field strength H_c2, superconductivity is destroyed. The mixed state is actually caused by vortices in the electronic superfluid, sometimes called fluxons because the flux carried by these vortices is quantized. Most pure elemental superconductors, except niobium, technetium, vanadium and carbon nanotubes, are Type I, while almost all impure and compound superconductors are Type II.