User:Halibutt/Spacetime/Mutual time dillation
Mutual time dilation and the twin paradox
[edit]Mutual time dilation
[edit]Click here for a brief section summary
Mutual time dilation and length contraction tend to strike beginners as inherently self-contradictory concepts. The worry is that if observer A measures observer B's clocks as running slowly, simply because B is moving at speed v relative to A, then the principle of relativity requires that observer B likewise measures A's clocks as running slowly. This is an important question that "goes to the heart of understanding special relativity."[1]: 198
Basically, A and B are performing two different measurements.
In order to measure the rate of ticking of one of B's clocks, A must use two of his own clocks, the first to record the time where B's clock first ticked at the first location of B, and second to record the time where B's clock emitted its second tick at the next location of B. Observer A needs two clocks because B is moving, so a grand total of three clocks are involved in the measurement. A's two clocks must be synchronized in A's frame. Conversely, B requires two clocks synchronized in her frame to record the ticks of A's clocks at the locations where A's clocks emitted their ticks. Therefore, A and B are performing their measurements with different sets of three clocks each. Since they are not doing the same measurement with the same clocks, there is no inherent necessity that the measurements be reciprocally "consistent" such that, if one observer measures the other's clock to be slow, the other observer measures the one's clock to be fast.[1]: 198–199
In regards to mutual length contraction, Fig. 2‑9 illustrates that the primed and unprimed frames are mutually rotated by a hyperbolic angle (analogous to ordinary angles in Euclidean geometry).[note 1] Because of this rotation, the projection of a primed meter-stick onto the unprimed x-axis is foreshortened, while the projection of an unprimed meter-stick onto the primed x′-axis is likewise foreshortened.

Fig. 2-10 reinforces previous discussions about mutual time dilation. In this figure, Events A and C are separated from event O by equal timelike intervals. From the unprimed frame, events A and B are measured as simultaneous, but more time has passed for the unprimed observer than has passed for the primed observer. From the primed frame, events C and D are measured as simultaneous, but more time has passed for the primed observer than has passed for the unprimed observer. Each observer measures the clocks of the other observer as running more slowly.[2]: 124
Please note the importance of the word "measure". An observer's state of motion cannot affect an observed object, but it can affect the observer's observations of the object.
In Fig. 2-10, each line drawn parallel to the x axis represents a line of simultaneity for the unprimed observer. All events on that line have the same time value of ct. Likewise, each line drawn parallel to the x′ axis represents a line of simultaneity for the primed observer. All events on that line have the same time value of ct′.
Twin paradox
[edit]Click here for a brief section summary
Elementary introductions to special relativity often illustrate the differences between Galilean relativity and special relativity by posing a series of supposed "paradoxes". All paradoxes are, in reality, merely ill-posed or misunderstood problems, resulting from our unfamiliarity with velocities comparable to the speed of light. The remedy is to solve many problems in special relativity and to become familiar with its so-called counter-intuitive predictions. The geometrical approach to studying spacetime is considered one of the best methods for developing a modern intuition.[3]
The twin paradox is a thought experiment involving identical twins, one of whom makes a journey into space in a high-speed rocket, returning home to find that the twin who remained on Earth has aged more. This result appears puzzling because each twin observes the other twin as moving, and so at first glance, it would appear that each should find the other to have aged less. The twin paradox sidesteps the justification for mutual time dilation presented above by avoiding the requirement for a third clock.[1]: 207 Nevertheless, the twin paradox is not a true paradox because it is easily understood within the context of special relativity.
The impression that a paradox exists stems from a misunderstanding of what special relativity states. Special relativity does not declare all frames of reference to be equivalent, only inertial frames. The traveling twin's frame is not inertial during periods when she is accelerating. Furthermore, the difference between the twins is observationally detectable: the traveling twin needs to fire her rockets to be able to return home, while the stay-at-home twin does not.[4]
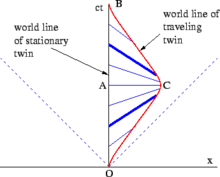
Deeper analysis is needed before we can understand why these distinctions should result in a difference in the twins' ages. Consider the spacetime diagram of Fig. 2‑11. This presents the simple case of a twin going straight out along the x axis and immediately turning back. From the standpoint of the stay-at-home twin, there is nothing puzzling about the twin paradox at all. The proper time measured along the traveling twin's world line from O to C, plus the proper time measured from C to B, is less than the stay-at-home twin's proper time measured from O to A to B. More complex trajectories require integrating the proper time between the respective events along the curve (i.e. the path integral) to calculate the total amount of proper time experienced by the traveling twin.[4]
Complications arise if the twin paradox is analyzed from the traveling twin's point of view.
For the rest of this discussion, we adopt Weiss's nomenclature, designating the stay-at-home twin as Terence and the traveling twin as Stella.[4]
We had previously noted that Stella is not in an inertial frame. Given this fact, it is sometimes stated that full resolution of the twin paradox requires general relativity. This is not true.[4]
A pure SR analysis would be as follows: Analyzed in Stella's rest frame, she is motionless for the entire trip. When she fires her rockets for the turnaround, she experiences a pseudo force which resembles a gravitational force.[4] Figs. 2‑6 and 2‑11 illustrate the concept of lines (planes) of simultaneity: Lines parallel to the observer's x-axis (xy-plane) represent sets of events that are simultaneous in the observer frame. In Fig. 2‑11, the blue lines connect events on Terence's world line which, from Stella's point of view, are simultaneous with events on her world line. (Terence, in turn, would observe a set of horizontal lines of simultaneity.) Throughout both the outbound and the inbound legs of Stella's journey, she measures Terence's clocks as running slower than her own. But during the turnaround (i.e. between the bold blue lines in the figure), a shift takes place in the angle of her lines of simultaneity, corresponding to a rapid skip-over of the events in Terence's world line that Stella considers to be simultaneous with her own. Therefore, at the end of her trip, Stella finds that Terence has aged more than she has.[4]
Although general relativity is not required to analyze the twin paradox, application of the Equivalence Principle of general relativity does provide some additional insight into the subject. We had previously noted that Stella is not stationary in an inertial frame. Analyzed in Stella's rest frame, she is motionless for the entire trip. When she is coasting her rest frame is inertial, and Terence's clock will appear to run slow. But when she fires her rockets for the turnaround, her rest frame is an accelerated frame and she experiences a force which is pushing her as if she were in a gravitational field. Terence will appear to be high up in that field and because of gravitational time dilation, his clock will appear to run fast, so much so that the net result will be that Terence has aged more than Stella when they are back together.[4] As will be discussed in the forthcoming section Curvature of time, the theoretical arguments predicting gravitational time dilation are not exclusive to general relativity. Any theory of gravity will predict gravitational time dilation if it respects the principle of equivalence, including Newton's theory.[1]: 16
- ^ a b c d Cite error: The named reference
Schutzwas invoked but never defined (see the help page). - ^ Cite error: The named reference
Collierwas invoked but never defined (see the help page). - ^ Schutz, Bernard F. (1985). A first course in general relativity. Cambridge, UK: Cambridge University Press. p. 26. ISBN 0521277035.
- ^ a b c d e f g Weiss, Michael. "The Twin Paradox". The Physics and Relativity FAQ. Retrieved 10 April 2017.
Cite error: There are <ref group=note> tags on this page, but the references will not show without a {{reflist|group=note}} template (see the help page).
