User:Infey7

Python

General

Running .py files in the interpreter

>>> exec(open('url.py').read())
Printing stuff...

Reloading modules

>>> import imp
>>> imp.reload(url)
Printing stuff...
<module 'url' from '.\\url.py'>

Adding directory to path

>>> import sys
>>> sys.path.append('C:\Python\Code')
>>> from url import parser

Finding variables and modules

>>> 'url' in globals().keys()
True

Dictionaries

>>> a = dict(first=1, second=2, third=3)
>>> b = {'first':1, 'second':2, 'third':3}
>>> a == b
True
>>> a['first']
1
>>> b['second']
2
>>> 'third' in a
True
>>> b.values()
dict_values([1, 2, 3])

Lists

>>> list = [2, 3, 4, 5]
>>> list.append(1)         # add to the end of list
>>> list
[2, 3, 4, 5, 1]
>>> list.sort()            # sort in ascending order
>>> list
[1, 2, 3, 4, 5]
>>> list.insert(0, 6)      # insert 6 at position 0
>>> list
[6, 1, 2, 3, 4, 5]
>>> list[:3]               # slice the list as desired
[6, 1, 2]
>>> list[3:5]
[3, 4]
>>> list.remove(4)         # remove the number 4 from the list
>>> list
[6, 1, 2, 3, 5]
>>> list.sort(reverse=True)
>>> list
[6, 5, 3, 2, 1]

Number conversion

>>> x=8
>>> y=bin(x)    # bin() will convert to a string
>>> y
'0b1000'
>>> type(y)
<class 'str'>
>>> int(y,2)    # cast to int with base 2
8

>>> import cmath
>>> z = 5-3j
>>> type(z)
<class 'complex'>
>>> r, phi = cmath.polar(z)    # convert complex to polar form
>>> r, phi
(5.830951894845301, -0.5404195002705842)
>>> cmath.rect(r, phi)         # convert polar form back to complex
(5-3.0000000000000004j)

For loops

>>> list = [1, 2, 3, 4, 5]
>>> for i in list:
...     print(i)
...
1
2
3
4
5

>>> for i in range(len(list)):
...     print(list[i])
...
1
2
3
4
5

Scipy and Numpy

Integrals

Consider the following integral:$\int _{0}^{4}\!2e^{3t}\,dt$

>>> import numpy as np
>>> func = lambda x: 2*np.exp(3*x)
>>> integrate.quad(func, 0, 4)
(108502.52761266934, 2.4994456113000214e-07)

Consider the following integral:$\int _{-\infty }^{\infty }\!e^{-|3t|}\,dt$

>>> func = lambda t: np.exp(-abs(3*t))
>>> integrate.quad(func, -np.inf, np.inf)
(0.6666666666666493, 7.022965268546203e-09)

Matrix operations

# Multiplication and dot product of two vectors
>>> a = np.array([1,2,3])
>>> b = np.array([4,5,6])
>>> a*b
array([ 4, 10, 18])
>>> np.dot(a, b)
32

# Find the inverse of a 3x3 matrix
>>> matrix = np.mat([[1,2,3],[4,5,6],[7,8,9]])
>>> matrix[0,:]
matrix([[1, 2, 3]])
>>> matrix[:,2]
matrix([[3],
        [6],
        [9]])
>>> inv = linalg.inv(matrix)
>>> inv
matrix([[ -4.50359963e+15,   9.00719925e+15,  -4.50359963e+15],
        [  9.00719925e+15,  -1.80143985e+16,   9.00719925e+15],
        [ -4.50359963e+15,   9.00719925e+15,  -4.50359963e+15]])

# Find the eigenvalues and eigenvectors of a 2x2 matrix
>>> b = np.mat([[1,1],[2,0]])
>>> d, v = linalg.eig(b)
>>> d
array([ 2., -1.])
>>> v
matrix([[ 0.70710678, -0.4472136 ],
        [ 0.70710678,  0.89442719]])

# Replace elements in a matrix
>>> f = np.ones((5,5))
>>> f
array([[ 1.,  1.,  1.,  1.,  1.],
       [ 1.,  1.,  1.,  1.,  1.],
       [ 1.,  1.,  1.,  1.,  1.],
       [ 1.,  1.,  1.,  1.,  1.],
       [ 1.,  1.,  1.,  1.,  1.]])
>>> r = np.array([2, 2, 2, 2, 2])
>>> f[1,:] = r
>>> f[:,0] = r
>>> f
array([[ 2.,  1.,  1.,  1.,  1.],
       [ 2.,  2.,  2.,  2.,  2.],
       [ 2.,  1.,  1.,  1.,  1.],
       [ 2.,  1.,  1.,  1.,  1.],
       [ 2.,  1.,  1.,  1.,  1.]])

Writing WAV files

from scipy.io.wavfile import write

def write_wave(duration, rate, freq, filename):
    period = rate / float(freq)
    omega = 2*np.pi / period
    t = np.arange(duration*rate, dtype=np.float)
    y = sp.sin(omega*t)
    
    # Normalize and convert to 16-bit integer
    z = np.int16(y/np.max(np.abs(y)) * 32767)
    sp.io.wavfile.write(filename, rate, z)

Math

Complex numbers

Rectangular form	Polar form	Exponential form
$x+jy\,$	$r\cdot (\cos \varphi +j\sin \varphi )$	$re^{j\varphi }\,$

$r={\sqrt {x^{2}+y^{2}}}$
$\varphi =\arctan(y/x)$

For polar form, $\varphi$ can be in degrees or radians. For exponential form, $\varphi$ must be in radians.

Complex to exponential

Example of transferring a complex representation to an exponential representation.

$x=-1+5j$
$\varphi =\arctan(5)=1.37{\text{ rad}}$
$\varphi =\pi -1.37=1.77$
$r={\sqrt {1^{2}+5^{2}}}={\sqrt {26}}=5.10$

$x=5.10e^{1.77j}$

Exponential to polar and rectangular

Here we transfer an exponential back to polar and rectangular form.

$x=2.50e^{3.84j}$
$3.84{\text{ rad}}=200{\text{ deg}}$
$2.50e^{3.84j}=2.50\cos(220)+j\sin(220)$

$x=2.50\cos(220)+j\sin(220)=1.92-1.61j$

Vectors

The dot product of two vectors results in a scalar. Two vectors are orthogonal if their dot product is zero.

$a={\begin{bmatrix}1\\2\\3\end{bmatrix}}{\text{ ,}}$ $b={\begin{bmatrix}4\\5\\6\end{bmatrix}}$

$\mathbf {a} \cdot \mathbf {b} =1*4+2*5+3*6=32$

The length of a vector is defined below.

$\left\|\mathbf {a} \right\|={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}={\sqrt {\mathbf {a} \cdot \mathbf {a} }}$

A unit vector (which has a length of 1) can be normalized as shown below.

$\mathbf {\hat {a}} ={\frac {\mathbf {a} }{\left\|\mathbf {a} \right\|}}$

Matrices

Reduction row echelon form (RREF)

Leading '1' is the only non-zero entry in the column; rows of all zeroes are at the bottom for style purposes.

$A=\left[{\begin{array}{cccc|c}1&2&1&1&7\\1&2&2&-1&12\\2&4&0&6&4\end{array}}\right]$
$A=\left[{\begin{array}{cccc|c}1&2&1&1&7\\0&0&-1&2&-5\\0&0&-2&4&-10\end{array}}\right]$
$A=\left[{\begin{array}{cccc|c}1&2&1&1&7\\0&0&1&-2&5\\0&0&-2&4&-10\end{array}}\right]$
$A=\left[{\begin{array}{cccc|c}1&2&1&1&7\\0&0&1&-2&5\\0&0&0&0&0\end{array}}\right]$
$A=\left[{\begin{array}{cccc|c}1&2&0&3&2\\0&0&1&-2&5\\0&0&0&0&0\end{array}}\right]$

Inverse

General algorithm

Create an augmented matrix with the identity matrix, then put the augmented matrix in RREF form. The inverse will be represented on the right side of the augmented matrix.

$A=\left[{\begin{array}{ccc|ccc}1&-1&-1&1&0&0\\-1&2&3&0&1&0\\1&1&4&0&0&1\end{array}}\right]$
$A=\left[{\begin{array}{ccc|ccc}1&-1&-1&1&0&0\\0&1&2&1&1&0\\0&2&5&-1&0&1\end{array}}\right]$
$A=\left[{\begin{array}{ccc|ccc}1&0&1&2&1&0\\0&1&2&1&1&0\\0&0&1&-3&-2&1\end{array}}\right]$
$A=\left[{\begin{array}{ccc|ccc}1&0&0&5&3&-1\\0&1&0&7&5&-2\\0&0&1&-3&-2&1\end{array}}\right]$

Formula

Formula for inverse of a 3x3 matrix

Computing ranks and bases

The Gaussian elimination algorithm can be applied to any $m\times n$ matrix $A$. In this way, for example, some $6\times 9$ matrices can be transformed to a matrix that has a row echelon form like

$T={\begin{bmatrix}a&*&*&*&*&*&*&*&*\\0&0&b&*&*&*&*&*&*\\0&0&0&c&*&*&*&*&*\\0&0&0&0&0&0&d&*&*\\0&0&0&0&0&0&0&0&e\\0&0&0&0&0&0&0&0&0\end{bmatrix}}$

where the *s are arbitrary entries and a, b, c, d, e are nonzero entries.

This echelon matrix $T$ contains a wealth of information about $A$: the rank of $A$ is 5 since there are 5 non-zero rows in $T$; the vector space spanned by the columns of $A$ has a basis consisting of the first, third, fourth, seventh and ninth column of $A$ (the columns of a, b, c, d, e in $T$), and the *s tell you how the other columns of $A$ can be written as linear combinations of the basis columns. This is a consequence of the distributivity of the dot product in the expression of a linear map.

Eigenvectors and eigenvalues

Eigenvectors and eigenvalues are related to matrix transformations. Specifically, certain transformations result in scalar multiples of the original vector.

$T({\overrightarrow {v}})=\tau ({\overrightarrow {v}})$
$\tau$ is the eigenvalue and $\tau ({\overrightarrow {v}})$ is the eigenvector

$\tau$ is an eigenvalue of A if and only if the determinant of $\tau (I_{n}-A)=0$
$A{\overrightarrow {v}}=\tau {\overrightarrow {v}}$
$0=\tau {\overrightarrow {v}}-A{\overrightarrow {v}}$
$0=\tau I_{n}{\overrightarrow {v}}-A{\overrightarrow {v}}$
$0=(\tau (I_{n})-A){\overrightarrow {v}}$

Calculating eigenvectors

Suppose we have the following eigenvalue of a given vector, and we want to calculate the corresponding unit length eigenvector.

$\tau =2{\text{ , }}B={\begin{bmatrix}1&1\\2&0\end{bmatrix}}$

$=2{\begin{bmatrix}1&0\\1&1\end{bmatrix}}-{\begin{bmatrix}1&1\\2&0\end{bmatrix}}$
$={\begin{bmatrix}2&0\\0&1\end{bmatrix}}-{\begin{bmatrix}1&1\\2&0\end{bmatrix}}$
$={\begin{bmatrix}1&-1\\-2&2\end{bmatrix}}$

Now translate the matrix to RREF form, and remember that $0=(\tau (I_{n})-A){\overrightarrow {v}}$
${\begin{bmatrix}1&-1\\0&0\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}$

$v_{1}-v_{2}=0$
$v_{1}=v_{2}$

If $\left\|\mathbf {v} \right\|=1$, then ${\sqrt {v_{1}^{2}+v_{2}^{2}}}=1$

${\sqrt {v_{1}^{2}+v_{2}^{2}}}=1$
$v_{1}^{2}+v_{2}^{2}=1$
$2v_{1}^{2}=1$
$v_{1}^{2}=1/2$
$v_{1}={\sqrt {1/2}}$
$v_{1}=v_{2}={\sqrt {1/2}}={\begin{bmatrix}1/{\sqrt {2}}\\1/{\sqrt {2}}\end{bmatrix}}$

Signal Processing

Polarization

Polarization refers to the orientation of the electric field during transmission. Remember the properties of electromagnetic wave, as illustrated below.

k is the direction of propagation, B is the magnetic field, E is the electric field

Additional Links

Antennas 101 - Video

Antenna Polarization

Phase Vocoder

Phase unwrapping

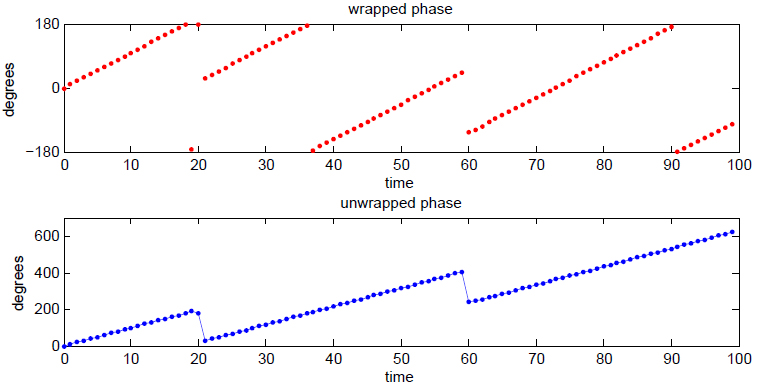
Multiples of 2 $\pi$ are discarded during the representation of a complex angle (based on the properties of the arctan function which will inherently "wrap" angles around the unit circle). If the phase were to be plotted, there would discontinuities (as shown below) when the phase crosses zero along the unit circle.

FFT frequency bins

Performing an FFT of 'N' samples will produce 'N' frequency bins, with an interval 'F/N' For real signal inputs, half of the frequency bins (from 'N/2 + 1' to 'N-1') are basically useless -- they are complex conjugates of the first half.

As an example, suppose we run the following code (with N = 1024 and F = 44100)...

>>> rate
44100
>>> len(frames[0])
1024
>>> fft = sp.fft(frames[0])

# Check to make sure we have 'N' bins
>>> len(fft)
1024

# The interval is 'F' / 'N'
>>> interval = rate / 1024
>>> abs(real(fft)).argmax()
12
>>> _ * interval
516.796875

# Can also be calculated using the fftfreq function
>>> freqs = sp.fftpack.fftfreq(frames[0].size, 1/rate)
>>> freqs[12]
516.796875

Phase code explained

We know the following facts:

- FFT of 'N' samples gives 'N' frequency bins

- Frequency interval between bins = rate/N

- Time for each sample = 1/rate

- Period = 1/F

- N/(1:N/2) is the length of the sinusoids at the center of bins 1:N/2 (remember that N/2 to N-1 are just complex conjugates)

- Therefore, bin 1 completes 1 cycle in N samples (N/1)

  .......... bin 2 completes 1 cycle in N/2 samples (N/2)

  .......... bin N/2 completes 1 cycle in 2 samples (N/(N/2))

We can show this with a bit of code:

# For bin 1
>>> rate = 44100
>>> fftSize = 1024
>>> time = 1/rate
>>> interval = rate/fftSize
>>> period = 1/interval
>>> period
0.023219954648526078
>>> time*fftSize
0.023219954648526078

# For bin 2
>>> rate = 44100
>>> fftSize = 1024
>>> time = 1/rate
>>> interval = rate/fftSize
>>> freq = interval*2
>>> period = 1/freq
>>> period
0.011609977324263039
>>> time*(fftSize/2)
0.011609977324263039

However, when calculating the phase shift, we must take into account the shift induced by our windowing:

- hopsize / (N/(1:N/2)) is the proportion of the cycle represented by the hop samples
- 2*pi*hopsize / (N/(1:N/2)) is that proportion in radians
- 2*pi*hopsize * ((1:N/2)/N) with cleaned up multiplication

Class notes

Eigenvectors of an LTI system (circulent matrix - finite length) are the complex harmonic sinusoids

Can stack the normalized eigenvectors into a matrix S that is NxN (complex) Can also create a frequency response matrix (F), which is a matrix of the corresponding eigenvalues along the diagonal

Where we wrote: y = Hx before, we can now write y = SFS(H)x