User:Silly rabbit/Sandbox/Exterior algebra

In mathematics, the exterior product or wedge product of vectors is an algebraic construction generalizing certain features of the cross product to higher dimensions. Like the cross product, and the scalar triple product, the exterior product of vectors is used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs. In linear algebra, the exterior product provides an abstract algebraic basis-independent manner for describing the determinant and the minors of a linear transformation, and is fundamentally related to ideas of rank and linear independence.

The exterior algebra (also known as the Grassmann algebra, after Hermann Grassmann) of a given vector space V is the algebra generated by the exterior product. It is widely used in contemporary geometry and multilinear algebra. In differential geometry, the exterior algebra arises naturally in the study of differential forms, and is used to provide algebraic characterizations of orientation and infinitesimal area (as needed in Stokes' theorem for example.) In algebraic geometry, it plays an important role in studies of projective space and other Grassmannians (see Plücker coordinates, for example.) In applications of ring theory to theoretical physics, it is the archetypal example of a superalgebra. In representation theory, it is a type of Schur functor, and is sometimes used as a tool to generate other Schur functors as well.

Formally, the exterior algebra is is a certain unital associative algebra over a field K which contains V as a subspace. It is denoted by Λ(V) or Λ^•(V) and its multiplication is also known as the wedge product or the exterior product and is written as $\wedge$. The wedge product is an associative and bilinear operation ∧ : Λ(V) × Λ(V) → Λ(V). Its essential feature is that it is alternating on V:

(1) $v\wedge v=0{\mbox{ for all }}v\in V,$

which implies in particular

(2) $u\wedge v=-v\wedge u$ for all $u,v\in V$, and

(3) $v_{1}\wedge v_{2}\wedge \cdots \wedge v_{k}=0$ whenever $v_{1},\ldots ,v_{k}\in V$ are linearly dependent.

Note that these three properties are only valid for the vectors in V, not for all elements of the algebra Λ(V).

Motivating examples

Areas in the plane

The area of a parallelogram in terms of the determinant of the matrix of coordinates of two of its vertices.

The Cartesian plane R² is a vector space equipped with a basis consisting of a pair of unit vectors

${\mathbf {e} }_{1}=(1,0),\quad {\mathbf {e} }_{2}=(0,1).$

Suppose that

$v=v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2},\quad w=w_{1}\mathbf {e} _{1}+w_{2}\mathbf {e} _{2}$

are a pair of given vectors in R², written in components. There is a unique parallelogram having v and w as two of its sides. The area of this parallelogram is given by the standard determinant formula:

$A=\left|\det {\begin{bmatrix}v&w\end{bmatrix}}\right|=|v_{1}w_{2}-v_{2}w_{1}|.$

Consider now the exterior product of v and w:

$v\wedge w=(v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2})\wedge (w_{1}\mathbf {e} _{1}+w_{2}\mathbf {e} _{2})=v_{1}w_{1}\mathbf {e} _{1}\wedge \mathbf {e} _{1}+v_{1}w_{2}\mathbf {e} _{1}\wedge \mathbf {e} _{2}+v_{2}w_{1}\mathbf {e} _{2}\wedge \mathbf {e} _{1}+v_{2}w_{2}\mathbf {e} _{2}\wedge \mathbf {e} _{2}$

$=(v_{1}w_{2}-v_{2}w_{1})\mathbf {e} _{1}\wedge \mathbf {e} _{2}$

where the first step uses the distributive law for the wedge product, and the last uses the fact that the wedge product is alternating. Note that the coefficient in this last expression is precisely the determinant of the matrix [v w]. The fact that this may be positive or negative has the intuitive meaning that v and w may be oriented in a counterclockwise or clockwise sense as the vertices of the parallelogram they define. Such an area is called the signed area of the parallelogram: the absolute value of the signed area is the ordinary area, and the sign determines its orientation.

The fact that this coefficient is the signed area is not an accident. In fact, it is relatively easy to see that the exterior product should be related to the signed area if one tries to axiomatize this area as an algebraic construct. In detail, if A(v,w) denotes the signed area of the parallelogram determined by the pair of vectors v and w, then A must satisfy the following properties:

1. A(av,bw) = a b A(v,w) for any real numbers a and b, since rescaling either of the sides rescales the area by the same amount (and reversing the direction of one of the sides reverses the orientation of the parallelogram).
2. A(v,v) = 0, since the area of the degenerate parallelogram determined by v (i.e., a line segment) is zero.
3. A(w,v) = -A(v,w), since interchanging the roles of v and w reverses the orientation of the parallelogram.
4. A(v + aw,w) = A(v,w), since adding a multiple of w to v affects neither the base nor the height of the parallelogram and consequently preserves its area.
5. A(e₁, e₂) = 1, since the area of the unit square is one.

With the exception of the last property, the wedge product satisfies the same formal properties as the area. In a certain sense, the wedge product generalizes the final property by allowing the area of a parallelogram to be compared to that of any "standard" chosen parallelogram. In other words, the exterior product in two-dimensions is a basis-independent formulation of area.

Cross and triple products

For vectors in R³, the exterior algebra is closely related to the cross product and triple product. Using the standard basis {e₁, e₂, e₃}, the wedge product of a pair of vectors

$\mathbf {u} =u_{1}\mathbf {e} _{1}+u_{2}\mathbf {e} _{2}+u_{3}\mathbf {e} _{3}$

and

$\mathbf {v} =v_{1}\mathbf {e} _{1}+v_{2}\mathbf {e} _{2}+v_{3}\mathbf {e} _{3}$

is

$\mathbf {u} \wedge \mathbf {v} =(u_{1}v_{2}-u_{2}v_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2})+(u_{1}v_{3}-u_{3}v_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{3})+(u_{2}v_{3}-u_{3}v_{2})(\mathbf {e} _{2}\wedge \mathbf {e} _{3})$

where {e₁ Λ e₂, e₁ Λ e₃, e₂ Λ e₃} is the basis for the three-dimensional space Λ²(R³). This imitates the usual definition of the cross product of vectors in three dimensions.

Bringing in a third vector

$\mathbf {w} =w_{1}\mathbf {e} _{1}+w_{2}\mathbf {e} _{2}+w_{3}\mathbf {e} _{3}$,

the wedge product of three vectors is

$\mathbf {u} \wedge \mathbf {v} \wedge \mathbf {w} =(u_{1}v_{2}w_{3}+u_{2}v_{3}w_{1}+u_{3}v_{1}w_{2}-u_{1}v_{3}w_{2}-u_{2}v_{1}w_{3}-u_{3}v_{2}w_{1})(\mathbf {e} _{1}\wedge \mathbf {e} _{2}\wedge \mathbf {e} _{3})$

where e₁ Λ e₂ Λ e₃ is the basis vector for the one-dimensional space Λ³(R³). This imitates the usual definition of the triple product.

The cross product and triple product in three dimensions each admit both geometric and algebraic interpretations. The cross product u×v can be interpreted as a vector which is perpendicular to both u and v and whose magnitude is equal to the area of the parallelogram determined by the two vectors. It can also be interpreted as the vector consisting of the minors of the matrix with columns u and v. The triple product of u, v, and w is geometrically a (signed) volume. Algebraically, it is the determinant of the matrix with columns u, v, and w. The exterior product in three-dimensions allows for similar interpretations. In fact, in the presence of a positively oriented orthonormal basis, the exterior product generalizes these notions to higher dimensions.

Formal definitions and algebraic properties

The exterior algebra Λ(V) over a vector space V is defined as the quotient algebra of the tensor algebra by the two-sided ideal I generated by all elements of the form $x\otimes x$ such that x ∈ V. Symbolically,

$\Lambda (V):=T(V)/(x\otimes x).$

The wedge product ∧ of two elements of Λ(V) is defined by

$\alpha \wedge \beta =\alpha \otimes \beta {\pmod {I}}.$

Anticommutativity of the wedge product

This product is anticommutative on elements of V, for supposing that x, y ∈ V,

$0\equiv (x+y)\wedge (x+y)=x\wedge x+x\wedge y+y\wedge x+y\wedge y\equiv x\wedge y+y\wedge x{\pmod {I}}$

whence

$x\wedge y=-y\wedge x.$

More generally, if x₁, x₂, ..., x_k are elements of V, and σ is a permutation of the integers [1,...,k], then

$x_{\sigma (1)}\wedge x_{\sigma (2)}\wedge \dots \wedge x_{\sigma (k)}={\rm {sgn}}(\sigma )x_{1}\wedge x_{2}\wedge \dots x_{k},$

where sgn(σ) is the signature of the permutation σ.

The exterior power

The k-th exterior power of V, denoted Λ^k(V), is the vector subspace of Λ(V) spanned by elements of the form

$x_{1}\wedge x_{2}\wedge \dots \wedge x_{k},\quad x_{i}\in V,i=1,2,\dots ,k.$

If α ∈ Λ^k(V), then α is said to be a k-multivector. If, furthermore, α can be expressed as a wedge product of k elements of V, then α is said to be decomposable. Although decomposable multivectors span Λ^k(V), not every element of Λ^k(V) is decomposable. For example, in R⁴, the following 2-multivector is not decomposable:

$\alpha =e_{1}\wedge e_{2}+e_{2}\wedge e_{3}+e_{3}\wedge e_{4}.$

(To see this, one need only check that α ∧ α ≠ 0.)

Basis and dimension

If the dimension of V is n and {e₁,...,e_n} is a basis of V, then the set

$\{e_{i_{1}}\wedge e_{i_{2}}\wedge \cdots \wedge e_{i_{k}}\mid 1\leq i_{1}<i_{2}<\cdots <i_{k}\leq n\}$

is a basis for Λ^k(V). The reason is the following: given any wedge product of the form

$v_{1}\wedge \cdots \wedge v_{k}$

then every vector v_j can be written as a linear combination of the basis vectors e_i; using the bilinearity of the wedge product, this can be expanded to a linear combination of wedge products of those basis vectors. Any wedge product in which the same basis vector appears more than once is zero; any wedge product in which the basis vectors do not appear in the proper order can be reordered, changing the sign whenever two basis vectors change places. In general, the resulting coefficients of the basis k-vectors can be computed as the minors of the matrix that describes the vectors v_j in terms of the basis e_i.

Counting the basis elements, we see that the dimension of Λ^k(V) is the binomial coefficient n choose k. In particular, Λ^k(V) = {0} for k > n.

Any element of the exterior algebra can be written as a sum of multivectors. Hence, as a vector space the exterior algebra is a direct sum

$\Lambda (V)=\Lambda ^{0}(V)\oplus \Lambda ^{1}(V)\oplus \Lambda ^{2}(V)\oplus \cdots \oplus \Lambda ^{n}(V)$

(where we set Λ⁰(V) = K and Λ¹(V) = V), and therefore its dimension is equal to the sum of the binomial coefficients, which is 2ⁿ.

Graded structure

The wedge product of a k-multivector with a p-multivector is a (k+p)-multivector, once again invoking bilinearity. As a consequence, the direct sum decomposition of the preceding section

$\Lambda (V)=\Lambda ^{0}(V)\oplus \Lambda ^{1}(V)\oplus \Lambda ^{2}(V)\oplus \cdots \oplus \Lambda ^{n}(V)$

gives the exterior algebra the additional structure of a graded algebra. Symbolically,

$\left(\Lambda ^{k}(V)\right)\wedge \left(\Lambda ^{p}(V)\right)\subset \Lambda ^{k+p}(V).$

Moreover, the wedge product is graded anticommutative, meaning that if α ∈ Λ^k(V) and β ∈ Λ^p(V), then

$\alpha \wedge \beta =(-1)^{pq}\beta \wedge \alpha .$

Universal property

Let V be a vector space over the field K (which in most applications will be the field of real numbers). The fact that Λ(V) is the "most general" unital associative K-algebra containing V with an alternating multiplication on V can be expressed formally by the following universal property:

Given any unital associative K-algebra A and any K-linear map j : V → A such that j(v)j(v) = 0 for every v in V, then there exists precisely one unital algebra homomorphism f : Λ(V) → A such that f(v) = j(v) for all v in V.

Universal property of the exterior algebra

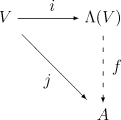
To construct the most general algebra that contains V and whose multiplication is alternating on V, it is natural to start with the most general algebra that contains V, the tensor algebra T(V), and then enforce the alternating property by taking a suitable quotient. We thus take the two-sided ideal I in T(V) generated by all elements of the form v⊗v for v in V, and define Λ(V) as the quotient

Λ(V) = T(V)/I

(and use Λ as the symbol for multiplication in Λ(V)). It is then straightforward to show that Λ(V) contains V and satisfies the above universal property.

As a consequence of this construction, the operation of assigning to a vector space V its exterior algebra Λ(V) is a functor from the category of vector spaces to the category of algebras.

Rather than defining Λ(V) first and then identifying the exterior powers Λ^k(V) as certain subspaces, one may alternatively define the spaces Λ^k(V) first and then combine them to form the algebra Λ(V). This approach is often used in differential geometry and is described in the next section.

Generalizations

Given a commutative ring R and an R-module M, we can define the exterior algebra Λ(M) just as above, as a suitable quotient of the tensor algebra T(M). It will satisfy the analogous universal property. Many of the properties of Λ(M) also require that M be a projective module. Where finite-dimensionality is used, the properties further require that M be finitely generated and projective.

Duality

Alternating operators

Given two vector spaces V and X, an alternating operator (or anti-symmetric operator) from V^k to X is a multilinear map

f: V^k → X

such that whenever v₁,...,v_k are linearly dependent vectors in V, then

f(v₁,...,v_k) = 0.

The most famous example is the determinant, an alternating operator from (Kⁿ)ⁿ to K.

The map

w: V^k → Λ^k(V)

which associates to k vectors from V their wedge product, i.e. their corresponding k-vector, is also alternating. In fact, this map is the "most general" alternating operator defined on V^k: given any other alternating operator f : V^k → X, there exists a unique linear map φ: Λ^k(V) → X with f = φ o w. This universal property characterizes the space Λ^k(V) and can serve as its definition.

Alternating multilinear forms

The above discussion specializes to the case when X = K, the base field. In this case an alternating multilinear function

f : V^k → K

is called an alternating multilinear form. The set of all alternating multilinear forms is a vector space, as the sum of two such maps, or the multiplication of such a map with a scalar, is again alternating. If V has finite dimension n, then this space can be identified with Λ^k(V^∗), where V^∗ denotes the dual space of V. In particular, the dimension of the space of anti-symmetric maps from V^k to K is the binomial coefficient n choose k.

Under this identification, and if the base field is R or C, the wedge product takes a concrete form: it produces a new anti-symmetric map from two given ones. Suppose ω : V^k → K and η : V^m → K are two anti-symmetric maps. As in the case of tensor products of multilinear maps, the number of variables of their wedge product is the sum of the numbers of their variables. It is defined as follows:

$\omega \wedge \eta ={\frac {(k+m)!}{k!\,m!}}{\rm {Alt}}(\omega \otimes \eta )$

where the alternation Alt of a multilinear map is defined to be the signed average of the values over all the permutations of its variables:

${\rm {Alt}}(\omega )(x_{1},\ldots ,x_{k})={\frac {1}{k!}}\sum _{\sigma \in S_{k}}{\rm {sgn}}(\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)})$

This definition of the wedge product is well-defined even if the fields K has finite characteristic, if one considers an equivalent version of the above that does not use factorials or any constants:

$\omega \wedge \eta (x_{1},\ldots ,x_{k+m})=\sum _{\sigma \in Sh_{k,m}}{\rm {sgn}}(\sigma )\,\omega (x_{\sigma (1)},\ldots ,x_{\sigma (k)})\eta (x_{\sigma (k+1)},\ldots ,x_{\sigma (k+m)})$,

where here $Sh_{k,m}\subset S_{k+m}$ is the subset of k,m shuffles: permutations $\sigma$ sending $1,2,\ldots ,k$ to numbers $\sigma (1)<\sigma (2)<\cdots <\sigma (k)$, and $k+1,k+2,\ldots ,k+m$ to numbers $\sigma (k+1)<\cdots <\sigma (k+m)$.

(Note. Some conventions, particularly in physics, define the wedge product as

$\omega \wedge \eta ={\rm {Alt}}(\omega \otimes \eta ).$

This convention is not adopted here, but see the Alternating tensor algebra section below for further details.)

Bialgebra structure

In formal terms, there is a correspondence between the graded dual of the graded algebra Λ(V) and alternating multilinear forms on V. The wedge product of multilinear forms defined above is dual to a coproduct defined on Λ(V), giving the structure of a coalgebra.

The coproduct is a linear function Δ : Λ(V) → Λ(V) ⊗ Λ(V) given on decomposable elements by

$\Delta (x_{1}\wedge \dots \wedge x_{k})=\sum _{p=0}^{k}\sum _{\sigma \in Sh_{p,k-p}}{\rm {sgn}}(\sigma )(x_{\sigma (1)}\wedge \dots \wedge x_{\sigma (p)})\otimes (x_{\sigma (p+1)}\wedge \dots \wedge x_{\sigma (k)}).$

This extends by linearity to an operation defined on the whole exterior algebra. In terms of the coproduct, the wedge product on the dual space is just the graded dual of the coproduct:

$(\alpha \wedge \beta )(x_{1}\wedge \dots \wedge x_{k})=(\alpha \otimes \beta )\left(\Delta (x_{1}\wedge \dots \wedge x_{k})\right)$

where the tensor product on the right-hand side is of multilinear linear maps (extended by zero on elements of incompatible homogeneous degree).

The counit is the homomorphism ε : Λ(V) → K which returns the 0-graded component of its argument. The coproduct and counit, along with the wedge product, define the structure of a bialgebra on the exterior algebra.

The interior product

See also: interior product

Suppose that V is finite-dimensional. If V* denotes the dual space to the vector space V, then for each α ∈ V^*, it is possible to define an antiderivation on the algebra Λ(V),

$i_{\alpha }:\Lambda ^{k}V\rightarrow \Lambda ^{k-1}V.$

This derivation is called the interior product with α, or sometimes the insertion operator.

Suppose that w ∈ Λ^kV. Then w is a multilinear mapping of V^* to R, so it is defined by its values on the k-fold Cartesian product V^*× V^*× ... × V^*. If u₁, u₂, ..., u_k-1 are k-1 elements of V^*, then define

$(i_{\alpha }{\mathbf {w} })(u_{1},u_{2}\dots ,u_{k-1})={\mathbf {w} }(\alpha ,u_{1},u_{2},\dots ,u_{k-1})$

Additionally, let i_αf = 0 whenever f is a pure scalar (i.e., belonging to Λ⁰V).

Axiomatic characterization and properties

The interior product satisfies the following properties:

1. For each k and each α ∈ V^*,

   $i_{\alpha }:\Lambda ^{k}V\rightarrow \Lambda ^{k-1}V.$

   (By convention, Λ^-1 = 0.)

2. If v is an element of V ( = Λ¹V), then i_αv = α(v) is the dual pairing between elements of V and elements of V^*.
3. For each α ∈ V^*, iα is a graded derivation of degree -1:

   $i_{\alpha }(a\wedge b)=(i_{\alpha }a)\wedge b+(-1)^{\deg a}a\wedge (i_{\alpha }b)$.

In fact, these three properties are sufficient to characterize the interior product as well as define it in the general infinite-dimensional case.

Further properties of the interior product include:

• $i_{\alpha }\circ i_{\alpha }=0.$
• $i_{\alpha }\circ i_{\beta }=-i_{\beta }\circ i_{\alpha }.$

The duality isomorphism

In general, there are two different kinds of alternating structures defined via duality:

• The structure of alternating multilinear forms on Λ(V). The space of all such forms is the graded dual Λ(V)^*, and the product of such forms dualizes the coproduct on the exterior algebra.
• The exterior algebra of the dual vector space Λ(V^*).

If V is finite-dimensional, then these two exterior algebras are naturally isomorphic.

Hodge duality

Main article: Hodge dual

Suppose that V has finite dimension n. Then the interior product induces a canonical isomorphism of vector spaces

$\Lambda ^{k}(V^{*})\otimes \Lambda ^{n}(V)\to \Lambda ^{n-k}(V).$

In the geometrical setting, an element of the top exterior power Λⁿ(V) (which is a one-dimensional vector space) is sometimes called a volume form (or orientation form, although this term may sometimes lead to ambiguity.) Relative to a given volume form σ, the isomorphism is given explicitly by

$\alpha \in \Lambda ^{k}(V^{*})\mapsto i_{\alpha }\sigma \in \Lambda ^{n-k}(V).$

If, in addition to a volume form, the vector space V is equipped with an inner product identifying V with V^*, then the resulting isomorphism is called the Hodge dual (or more commonly the Hodge star operator)

$*:\Lambda ^{k}(V)\rightarrow \Lambda ^{n-k}(V).$

The composite of * with itself maps Λ^k(V) → Λ^k(V) and is always a scalar multiple of the identity map. In most applications, the volume form is compatible with the inner product in the sense that it is a wedge product of an orthonormal basis of V. In this case,

$*\circ *:\Lambda ^{k}(V)\to \Lambda ^{k}(V)=(-1)^{k(n-k)+q}I$

where I is the identity, and the inner product has metric signature (p,q) — p plusses and q minuses.

Along with the bialgebra structure, the Hodge star operator on Λ(V) defines the antipode map for a Hopf algebra on the exterior algebra.

Functoriality

Suppose that V and W are a pair of vector spaces and f : V → W is a linear transformation. Then, by the universal construction, there exists a unique homomorphism of graded algebras

$\Lambda (f):\Lambda (V)\rightarrow \Lambda (W)$

such that

$\Lambda (f)|_{\Lambda ^{1}(V)}=f:V=\Lambda ^{1}(V)\rightarrow W=\Lambda ^{1}(W).$

In particular, Λ(f) preserves homogeneous degree. The k-graded components of Λ(f) are given on decomposable elements by

$\Lambda (f)(x_{1}\wedge \dots \wedge x_{k})=f(x_{1})\wedge \dots \wedge f(x_{k}).$

Let

$\Lambda ^{k}(f)=\Lambda (f)_{\Lambda ^{k}(V)}:\Lambda ^{k}(V)\rightarrow \Lambda ^{k}(W).$

The components of the transformation Λ(k) relative to a basis of V and W is the matrix of k × k minors of f. In particular, if V = W and V is of finite dimension n, then Λⁿ(f) is a mapping of a one-dimensional vector space Λⁿ to itself, and is therefore given by a scalar: the determinant of f.

Exactness

The functor Λ is exact, meaning that if

$0\rightarrow U\rightarrow V\rightarrow W\rightarrow 0$

is a short exact sequence of vector spaces, then

$0\rightarrow \Lambda (U)\rightarrow \Lambda (V)\rightarrow \Lambda (W)\rightarrow 0$

is also exact.

One consequence of the exactness is that the exterior powers of a direct sum of two vector spaces decompose into tensor products:

$\Lambda ^{k}(V\oplus W)=\bigoplus _{a+b=k}\Lambda ^{a}(V)\otimes \Lambda ^{b}(W).$

Furthermore, if

$0\to U\to V\to W\to 0$

is an exact sequence of vector spaces, with dim(U) = a, dim(V) = a+b, and dim(W) = b, then

$\Lambda ^{a+b}(V)=\Lambda ^{a}(U)\otimes \Lambda ^{b}(W).$

The alternating tensor algebra

If K is a field of characteristic 0, then the exterior algebra of a vector space V can be canonically identified with the vector subspace of T(V) consisting of antisymmetric tensors. Recall that the exterior algebra is the quotient of T(V) by the ideal I generated by x ⊗ x.

Let T^r(V) be the space of homogeneous tensors of rank r. This is spanned by decomposable tensors

$v_{1}\otimes \dots \otimes v_{r},\quad v_{i}\in V.$

The antisymmetrization (or sometimes the skew-symmetrization) of a decomposable tensor is defined by

${\text{Alt}}(v_{1}\otimes \dots \otimes v_{r})={\frac {1}{r!}}\sum _{\sigma \in {\mathfrak {S}}_{r}}{\rm {sgn}}(\sigma )x_{\sigma (1)}\otimes \dots \otimes x_{\sigma (r)}$

where the sum is taken over the symmetric group of permutations on the symbols {1,...,r}. This extends by linearity and homogeneity to an operation, also denoted by Alt, on the full tensor algebra T(V). The image Alt(T(V)) is the alternating tensor algebra, denoted A(V). This is a vector subspace of T(V), and it inherits the structure of a graded vector space from that on T(V). It carries an associative graded product ${\widehat {\otimes }}$ defined by

$t{\widehat {\otimes }}s={\text{Alt}}(t\otimes s).$

Although this product differs from the tensor product, the kernel of Alt is precisely the ideal I (again, assuming that K has characteristic 0), and there is a canonical isomorphism

$A(V)\cong \Lambda (V).$

Index notation

Suppose that V has finite dimension n, and that a basis e₁, ..., e_n of V is given. then any alternating tensor t ∈ A^r(V) ⊂ T^r(V) can be written in index notation as

$t=t^{i_{1}i_{2}\dots i_{r}}\,{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \dots \otimes {\mathbf {e} }_{i_{r}}$

where t^i₁...i_r is completely antisymmetric in its indices.

The wedge product of two alternating tensors t and s of ranks r and p is given by

$t{\widehat {\otimes }}s={\frac {1}{(r+p)!}}\sum _{\sigma \in {\mathfrak {S}}_{r+p}}t^{i_{\sigma (1)}\dots i_{\sigma (r)}}s^{i_{\sigma (r+1)}\dots i_{\sigma (r+p)}}{\mathbf {e} }_{i_{1}}\otimes {\mathbf {e} }_{i_{2}}\otimes \dots \otimes {\mathbf {e} }_{i_{r+p}}.$

The components of this tensor are precisely the skew part of the components of the tensor product s ⊗ t, denoted by square brackets on the indices:

$(t{\widehat {\otimes }}s)^{i_{1}\dots i_{r+p}}=t^{[i_{1}\dots i_{r}}s^{i_{r+1}\dots i_{r+p}]}$

The interior product may also be described in index notation as follows. Let $t=t^{i_{0}i_{1}\dots i_{k-1}}$ be an antisymmetric tensor of rank k. Then, for α ∈ V^*, i_αw is an alternating tensor of rank k-1, given by

$(i_{\alpha }t)^{i_{1}\dots i_{k-1}}=k\sum _{j=0}^{n}\alpha _{j}w^{ji_{1}\dots i_{k-1}}$.

where n is the dimension of V.

Applications

Linear geometry

The decomposable k-vectors have geometric interpretations: the bivector $u\wedge v$ represents the plane spanned by the vectors, "weighted" with a number, given by the area of the oriented parallelogram with sides u and v. Analogously, the 3-vector $u\wedge v\wedge w$ represents the spanned 3-space weighted by the volume of the oriented parallelepiped with edges u, v, and w.

Differential geometry

The exterior algebra has notable applications in differential geometry, where it are used to define differential forms. A differential forms can intuitively be interpreted as a function on weighted subspaces of the tangent space of a differentiable manifold. As a consequence, there is a natural wedge product for differential forms. Differential forms play a major role in diverse areas of differential geometry.

Physics

The exterior algebra is an archetypal example of a superalgebra, which plays a fundamental role in physical theories pertaining to fermions and supersymmetry. For a physical discussion, see Grassmann number. For various other applications of related ideas to physics, see superspace and supergroup (physics).

History

The exterior algebra was first introduced by Hermann Grassmann in 1844 under the blanket term of Ausdehnungslehre, or Theory of Extension. This referred more generally to an algebraic (or axiomatic) theory of extended quantities and was one of the early precursors to the modern notion of a vector space.

The algebra itself was built from a set of rules, or axioms, capturing the formal aspects of Cayley and Sylvester's theory of multivectors. It was thus a calculus, much like the propositional calculus, except focused exclusively on the task of formal reasoning in geometrical terms. In particular, this new development allowed for an axiomatic characterization of dimension, a property that had previously only been examined from the coordinate point of view.

The import of this new theory of vectors and multivectors was lost to mid 19th century mathematicians, until being thoroughly vetted by Giuseppe Peano in 1888. Peano's work also remained somewhat obscure until the turn of the century, when the subject was unified by members of the French geometry school (notably Henri Poincaré, Elie Cartan, and Gaston Darboux) who applied Grassmann's ideas to the calculus of differential forms.

A short while later, Alfred North Whitehead, borrowing from the ideas of Peano and Grassmann, introduced his universal algebra. This then paved the way for the 20th century developments of abstract algebra by placing the axiomatic notion of an algebraic system on a firm logical footing.

References

Mathematical references

• Bishop, R. and Goldberg, S.I. (1980). Tensor analysis on manifolds. Dover. ISBN 0-486-64039-6.{{cite book}}: CS1 maint: multiple names: authors list (link)

Includes a treatment of alternating tensors and alternating forms, as well as a detailed discussion of Hodge duality from the perspective adopted in this article.

• Bourbaki, Nicolas (1989). Elements of mathematics, Algebra I. Springer-Verlag. ISBN 3-540-64243-9.

This is the main mathematical reference for the article. It introduces the exterior algebra of a module over a commutative ring (although this article specializes primarily to the case when the ring is a field), including a discussion of the universal property, functoriality, duality, and the bialgebra structure. See chapters III.7 and III.11.

• MacLane, S. and Birkhoff, G. (1999). Algebra. AMS Chelsea. ISBN 0-8218-1646-2.{{cite book}}: CS1 maint: multiple names: authors list (link)

Chapter XVI sections 6-10 give a more elementary account of the exterior algebra, including duality, determinants and minors, and alternating forms.

• Sternberg, Shlomo (1964). Lectures on Differential Geometry. Prentice Hall.

Contains a classical treatment of the exterior algebra as alternating tensors, and applications to differential geometry.

Historical references

• Bourbaki, Nicolas (1989). "Historical note on chapters II and III". Elements of mathematics, Algebra I. Springer-Verlag.
• Browne, J.M. (2007). Grassmann algebra - Exploring applications of Extended Vector Algebra with Mathematica. Published on line. {{cite book}}: External link in |publisher= (help)
• Clifford, W. (1878). "Applications of Grassmann's Extensive Algebra". American Journal of Mathematics. 1 (4): 350–358.
• Forder, H. G. (1941). The Calculus of Extension. Cambridge University Press.
• Grassmann, Hermann (1844). Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik. {{cite book}}: External link in |title= (help) (The Linear Extension Theory - A new Branch of Mathematics)
• Grassmann, Hermann (2000). Extension Theory (translation by L.C. Kannenberg). American Mathematical Society. ISBN 0821820311.
• Peano, Giuseppe (1888). Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva. [Geometric Calculus according to Grassmann's Ausdehnungslehre, preceded by the Operations of Deductive Logic]
• Whitehead, Alfred North (1898). A Treatise on Universal Algebra, with Applications. Cambridge.

See also

• multilinear algebra
• tensor algebra
• symmetric algebra
• Clifford algebra
• geometric algebra
• Koszul complex

Category:Multilinear algebra Category:Differential forms