Mathematics desk
< December 18	<< Nov \| December \| Jan >>	December 20 >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

December 19

Are these groups isomorph to $(\mathbb {Q} ,+)$

Assume $\forall m,n\in \mathbb {N}$

${\begin{cases}n\star 1=n\\(2n)\star (2n+1)=1\\(2n)\star (2m)=2n+2m\\(2n+1)\star (2m+1)=2n+2m+1\\(2n)\star (2m+1)={\begin{cases}2m-2n+1&2m+1>2n\\2n-2m&2n>2m+1\end{cases}}\end{cases}}$

It is clear $(\mathbb {N} ,\star )$ is a cyclic group, $\langle 2\rangle =(\mathbb {N} ,\star )\cong (\mathbb {Z} ,+).$ and let $Q_{1}=\left\{{m \over n}\,|\,m,n\in \mathbb {N} \right\}$ , it is clear $(Q_{1},\star _{1})$ is an Abelian group with:

${\begin{cases}\forall m,n,u,v\in \mathbb {N} \\({m \over n})\star _{1}1={m \over n}\\({m \over n})^{-1}={m^{-1} \over n^{-1}}\qquad m\star m^{-1}=1=n\star n^{-1}\\{m \over n}\star _{1}{u \over v}={m_{1} \over n_{1}}\star _{1}{u_{1} \over v_{1}}={{m_{1}\star u_{1}} \over {n_{1}\star v_{1}}}\quad {\text{if}}\,\,{\begin{cases}{m \over n}={m_{1} \over n_{1}},\,\,{u \over v}={u_{1} \over v_{1}},\,\,{mu \over nv}={m_{1}u_{1} \over n_{1}v_{1}}\\\gcd(m_{1},n_{1})=\gcd(m_{1},v_{1})=1\\\gcd(u_{1},n_{1})=\gcd(u_{1},v_{1})=1\end{cases}}\end{cases}}$

Question: does $(Q_{1},\star _{1})\cong (\mathbb {Q} ,+)$ ?

$\color {red}{Problem:}$ Suppose $N_{1}=\{(m,n)\,|\,m,n\in \mathbb {N} ,\,\gcd(m,n)=1\}$ , make a group on $N_{1}$ correspondence to $(Q_{1},\star _{1})$ in terms of members production and isomorph to $(Q_{1},\star _{1})$ .

Thanks in advance. Alireza Badali (talk) 15:13, 19 December 2017 (UTC)[reply]

Your second set can't be a group unless you're adding the multiplicative inverses

m_{i}^{-1}

to

N_{1}

.--Jasper Deng (talk) 09:12, 20 December 2017 (UTC)[reply]

Thank you, so I remodeled the latter question. Alireza Badali (talk) 13:43, 20 December 2017 (UTC)[reply]

Is there any motivation for this question? Does it come from somewhere? A class assignment? --JBL (talk) 16:43, 20 December 2017 (UTC)[reply]

No it isn't a class assignment only I want make a group on

\mathbb {N}

isomorph to

(\mathbb {Q} ,+)

, of course probably I won't succeed because I have reached to another open problem but I want prepare way towards it. Alireza Badali (talk) 17:45, 20 December 2017 (UTC)[reply]

"I want" -- why do you want this? What is the point of this activity? It is easy to write down formally such an operation (I've done it below), but so what? --JBL (talk) 18:12, 21 December 2017 (UTC)[reply]

Purpose is the formula of prime numbers but for it I think Goldbach's conjecture and Polignac's conjecture and tuple is needed, but most important is Goldbach and for it I am theorizing of course it is very unlikely and remote I will succeed! of course in addition to this question below question should be answered but it is impossible:

$\color {red}{[[[}$ Question: To define an Abelian group structure on $\mathbb {N}$ that is not a finitely generated Abelian group and is isomorph to $(\mathbb {Q} ,+)$ , I need to know what is function of a subsequence of $(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),...,(1,2k-2),$ $(2,2k-3),...,(k-1,k),(k,k-1),...,(2k-3,2),(2k-2,1),(1,2k-1),(2,2k-2),$ $...,(k-1,k+1),(k,k),(k+1,k-1),...,(2k-2,2),(2k-1,1),...$ such that $(u,v)$ is belong to this subsequence iff gcd $(u,v)=1$ as: $(1,1),(1,2),(2,1),(1,3),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(5,1),(1,6),(2,5),(3,4),(4,3),$ $(5,2),(6,1),(1,7),(3,5),(5,3),(7,1),...\color {red}{]]]}$ Alireza Badali (talk) 19:34, 21 December 2017 (UTC)[reply]

I'm not sure how the *₁ operation is supposed to work. For example, what is (2/3) *₁ (3/4)? The condition says 2n₁ = 3m₁, 3v₁ = 4u₁, so m₁ and v₁ are even and GCD(m₁, v₁) = 1 is impossible. --RDBury (talk) 15:23, 20 December 2017 (UTC)[reply]

I mean is first simplification of fractions and then calculation like

{44 \over 12}

that gets

{11 \over 3}

. Alireza Badali (talk) 17:45, 20 December 2017 (UTC)[reply]

Per the 17:45, 20 December 2017 (UTC) reply, the real question seems to be "find a binary operation * on N such that (N,*) is homomorph to (Q,+)". ~~While I have no proof of that, my money is on the proposition that no such operation exists.~~ Tigraan^{Click here to contact me} 14:19, 21 December 2017 (UTC)[reply]

Of course such an operation exists: take any bijection f between N and Q, and define * by (a * b) = f^{-1}(f(a) + f(b)). Why anyone would want to write such a thing down explicitly, though, is a total mystery. --JBL (talk) 14:51, 21 December 2017 (UTC)[reply]

Huh... I actually meant to require (N,*) to be a group. I thought the structure would "obviously" be lost by the bijection, but that is not the case (per above). Tigraan^{Click here to contact me} 12:49, 22 December 2017 (UTC)[reply]

Why not, maybe more, even algebraic numbers! and more and more and more! Alireza Badali (talk) 17:30, 21 December 2017 (UTC)[reply]

This comment is incomprehensible, and it is also not clear to whom it is directed. --JBL (talk) 18:12, 21 December 2017 (UTC)[reply]

I mean is making group on algebraic numbers by using natural numbers or on some other undiscovered larger countable subsets of real numbers and larger and again larger and so on until the last but the philosophy is that: thinking on finite sets is normal and on countable sets is possible but about uncountable sets is imagination unless after than discovering of formula of prime numbers a good definition of transcendental numbers be obtained and so on that I can not say or think or imagine

\color {green}{!}

Alireza Badali (talk) 19:46, 21 December 2017 (UTC)[reply]

What is a lampshade?

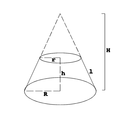
In an earlier question I found out a pyramid with a flat top, like those in Mexico, was called a frustum. What do you call it when the same thing happens to a cone?— Vchimpanzee • talk • contributions • 21:49, 19 December 2017 (UTC)[reply]

Frustum, or perhaps conical frustum or even right circular conical frustrum if you wish to be more specific. Interestingly, while our article discusses and gives formulae for them, none of the illustrations are of circular conical frustums. -- ToE 21:56, 19 December 2017 (UTC)[reply]

See conical image-ish at Frustum#Examples. hydnjo (talk) 16:51, 20 December 2017 (UTC)[reply]

@Vchimpanzee: Do you mean something like these?

'Trunctated cone'
'Cropped cone'

--CiaPan (talk) 17:21, 20 December 2017 (UTC)[reply]

Yes, that's exactly what I mean. Thank you.— Vchimpanzee • talk • contributions • 14:34, 21 December 2017 (UTC)[reply]

December 19

Are these groups isomorph to ( Q , + ) {\displaystyle (\mathbb {Q} ,+)}

What is a lampshade?

Are these groups isomorph to $(\mathbb {Q} ,+)$