Mathematics desk
< October 22	<< Sep \| October \| Nov >>	Current desk >

Welcome to the Wikipedia Mathematics Reference Desk Archives
The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages.

October 23[edit]

Klein bottle colouring exception[edit]

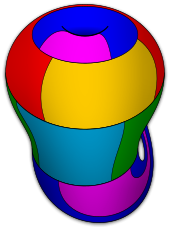
Would anyone here know if it's proven that the Klein bottle is the only exception to the Heawood conjecture?

I added this diagram to the article and wondered if the caption should read "A 6-colored Klein bottle, the only known exception to the Heawood conjecture" instead.

Thanks,
cmɢʟee⎆τaʟκ 17:43, 23 October 2021 (UTC)[reply]

@Cmglee: The article states This relation holds, as Ringel and Youngs showed, for all surfaces except for the Klein bottle. Philip Franklin (1930) proved that the Klein bottle requires at most 6 colors, rather than 7 as predicted by the formula so it would seem that it's proven to be the only counterexample. eviolite (talk) 20:49, 23 October 2021 (UTC)[reply]

Thank you very much, @Eviolite:. The current caption is correct, then. Cheers, cmɢʟee⎆τaʟκ 01:14, 24 October 2021 (UTC)[reply]

Resolved

Confusing Bayesian principle[edit]

In this video the Bayesian argument seems to be that every guess brings one closer to the actual location of the ball insofar as we are able to compare it to some reference point. But how does that actually help? Assume for example a very large table where the thrower happens to be particularly bad at tossing a ball. Now suppose that the original guess is in fact 100% correct. Surely each successive guess could possibly move the point further and further away from the actual position? Earl of Arundel (talk) 19:10, 23 October 2021 (UTC)[reply]

It is a bit longish and boring to watch the whole thing, but isn't the argument that every test increases one's confidence in (the refined guesses of) its location? So, in statistical terms, in the limit the locations of one's successive updated distributions tend to the true location, while the corresponding confidence regions contract to a point. One of the comments on the video quips, "With every throw, you get more and more information. For instance, that you needed a bigger table." But, actually, a large table would invalidate the experiment. It only works because the table is smallish. Some unspecified but strong conditions (including the independence of successive tests) need to be added to make this a theorem, and then this is the Bayesian counterpart of the central limit theorem of (non-Bayesian) probability theory. --Lambiam 09:43, 24 October 2021 (UTC)[reply]

Ok so as is the claim is somewhat dubious. Well that's rather disappointing. I would have expected a little more rigor from such a popular maths channel! Oy vey...Earl of Arundel (talk) 13:26, 24 October 2021 (UTC)[reply]

But do they actually state at any time that every guess brings one closer to the actual location? --Lambiam 17:12, 24 October 2021 (UTC)[reply]

Maybe not but either way it kind of calls in to question the actual utility (or even relevance) of such an approach. Perhaps it is somewhat applicable to understanding vague properties of metric spaces or some such. It doesn't really seem to be a very intriguing fact quite frankly. The "classic" formulation of Bayes' theorem is much more interesting imo... Earl of Arundel (talk) 18:10, 24 October 2021 (UTC)[reply]

The point of the video – if I understood correctly – is that the experiment shown is the dramatized execution of a thought experiment described by the reverend Thomas Bayes in the manuscript in which he described the basic idea, unpublished during his lifetime and probably written in the late 1750s. Bayes' formulation of the theorem was in terms of the prior and posterior distribution of the (unknown) parameter of the binomial distribution. The (much more general) "classic" formulation of Bayes' theorem in explicit terms of conditional probabilities is, I think, due to Laplace (1814). --Lambiam 19:23, 24 October 2021 (UTC)[reply]

I see. So this was the initial insight that would eventually lead Laplace and others to develop the idea further into what we now know of as Bayesian statistics which is of course arguably one of the most important subfields of mathematics. Well I can certainly appreciate that! I still say the Gedanken experiment itself is just a bit too vague. Without better constraints it almost seems paradoxical... Earl of Arundel (talk) 17:33, 25 October 2021 (UTC)[reply]