Wikipedia:Reference desk/Archives/Mathematics/2024 February 18
| Mathematics desk | ||
|---|---|---|
| < February 17 | << Jan | February | Mar >> | Current desk > |
| Welcome to the Wikipedia Mathematics Reference Desk Archives |
|---|
| The page you are currently viewing is a transcluded archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
February 18[edit]
Cramer's paradox[edit]
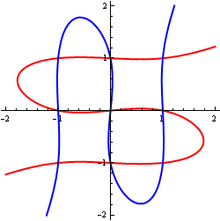
Cramer's paradox states:
| “ | Cramer pointed out that the cubic curves and intersect in precisely nine points. | ” |
When I plotted the curves, I found only three intersects.
The plot in the article (right) has nine intersects but the curves don't look cubic but rather contrived to intersect at the required points:
What is the mistake in my understanding?
Thanks, cmɢʟee⎆τaʟκ 15:12, 18 February 2024 (UTC)
- You plotted (in blue) the curve defined by the equation which is very different from Cramer's equation.*
- so its graph is the union of the three graphs for and each of which is a vertical line. --Lambiam 16:57, 18 February 2024 (UTC)
- *I cannot find an RS for the statement this example is due to Cramer. It is used by Sandifer (see Extermal links), who does not give an attribution. --Lambiam 19:24, 18 February 2024 (UTC)
- If you want an illustration with non-degenerate cubics, this will do:
- Using a blow-up factor of instead of or in fact any factor strictly larger than , already gives nine points of intersection. The best choice is more a matter of esthetics. --Lambiam 17:55, 18 February 2024 (UTC)
- You might have to use the complex projective plane or have duplicate points to get all the points. Circular points at infinity is an interesting case which gives two extra points where circles intersect besides the obvious ones. NadVolum (talk) 18:15, 18 February 2024 (UTC)
- Possibly prettier:
- Then the graph of the second curve is not mirrored along the diagonal but rotated by a quarter turn. In this case the critical value for the blow-up factor is larger than the previous ; it equals --Lambiam 18:53, 18 February 2024 (UTC)
- FWIW, the equations of the curves given in the illustration are x3 - x = 10(y3 - y) and y3 - y = 10(x3 - x). The Mathematica source code for the plot is given on the file information page.
- Bezout's theorem says that any two cubics, assuming a few non-degeneracy conditions, have 9 points of intersection, if multiplicities, imaginary points, and points at infinity are counted correctly. This would apply to the curves in the upper left as well, so even though only three points of intersection are visible there should be more. It might be an interesting exercise to find them. I'm thinking the origin has multiplicity more than 1, so that accounts for at least some of the missing ones. --RDBury (talk) 09:22, 19 February 2024 (UTC)
- (Solution to exercise) The 9 points of intersection are (0, 0) with multiplicity 3, (√2, √2), (-√2, -√2), (eiπ/12, ei5π/12), (ei5π/12, eiπ/12), (e-iπ/12, e-i5π/12), (e-i5π/12, e-iπ/12). So there are two accounted for by multiplicity, and 4 which are complex and so not visible on the graph. --RDBury (talk) 09:50, 19 February 2024 (UTC)
- Thank you very much, everyone. I understand now, and have updated my diagram to Cramer's degenerate cubics. Cheers, cmɢʟee⎆τaʟκ 14:34, 20 February 2024 (UTC)
- If they are Cramer's; I can't find a reliable source for the statement this example is due to Cramer. --Lambiam 20:02, 20 February 2024 (UTC)
- According to this site, the three lines example is actually due to Euler. In fact all curves of the form A(x3+x)+B(y3+y)=0, several of which have been mentioned here, intersect in the same nine points. The example isn't the paradox though, it's just an example of it. It might be worth mentioning that the statement of Cramer's paradox given in the the original question is not the correct statement. It's really two general theorems about cubic and higher order curves that seem to contradict each other.
1) Cramer's theorem: n(n+3)/2 points determine a curve of order n.
2) Bézout's theorem: Two curves of order n intersect in n2 points.
This is a seeming contradiction for n2 ≥ n(n+3)/2, in other words for n≥3. --RDBury (talk) 06:33, 21 February 2024 (UTC)- @RDBury: I have added three HTML line-breaks to your comment above to make the two theorems more prominent. Feel free to revert my change if you don't like it. --CiaPan (talk) 07:20, 21 February 2024 (UTC)
- Thanks. I also added the title Bézout's theorem to the second statement, though it wasn't known as that when Cramer and Euler were working on the issue. I just read the Bradley & Stemkoski paper given in the link above and added it to "Enternal links" section of the article; it seems like an excellent summary of the topic and well worth mining for material to include in our article, in particular Cayley's theorem mentioned near the end. The GeoGebra applets seem especially instructive and I wonder if it's possible to include them in Wikipedia. I'm guessing there would be technical or copyright issues with that. --RDBury (talk) 08:09, 21 February 2024 (UTC)
- Euler's example of a 9-point set in is a counterexample to an unqualified statement of Cramer's theorem, which holds generically but not universally. It is a counterexample because it does not determine a unique cubic but a whole family characterized by the parametrized set of equations . One doesn't need Bézout's theorem to see this. Any pair of independent cubics from this family can be chosen as an illustration; none of these pairs can IMO be called an example "due to Euler". --Lambiam 09:24, 21 February 2024 (UTC)
- @RDBury: I have added three HTML line-breaks to your comment above to make the two theorems more prominent. Feel free to revert my change if you don't like it. --CiaPan (talk) 07:20, 21 February 2024 (UTC)
- According to this site, the three lines example is actually due to Euler. In fact all curves of the form A(x3+x)+B(y3+y)=0, several of which have been mentioned here, intersect in the same nine points. The example isn't the paradox though, it's just an example of it. It might be worth mentioning that the statement of Cramer's paradox given in the the original question is not the correct statement. It's really two general theorems about cubic and higher order curves that seem to contradict each other.
- If they are Cramer's; I can't find a reliable source for the statement this example is due to Cramer. --Lambiam 20:02, 20 February 2024 (UTC)
@Cmglee: I would just point out that the fact that you went and changed the image on the left makes it very hard to follow your original question for someone looking at the discussion after the fact. Before this question gets archived, you might put in a note somewhere saying "here is the original image" and reproducing it, or something. (It's especially confusing since you have the original caption that says "[o]nly three intersects?" in a picture that clearly has nine — I puzzled over that for some time.) --Trovatore (talk) 07:33, 22 February 2024 (UTC)
- Good point, @Trovatore: I've updated my question accordingly. cmɢʟee⎆τaʟκ 12:59, 22 February 2024 (UTC)
- Note that the change was not made here but at the Commons; its changing here was a (probably not intended) side effect. --Lambiam 13:38, 22 February 2024 (UTC)





















