Wild arc

The Fox-Artin wild arc lying in R³ Note that each "tail" of the arc is converging to a point.

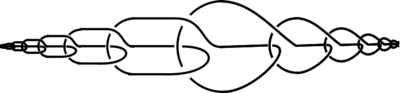
In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to a straight line segment. Antoine (1920) found the first example of a wild arc, and Fox & Artin (1948) found another example called the Fox–Artin arc whose complement is not simply connected.

See also

• Wild knot

Further reading

• Antoine, L. (1920), "Sur la possibilité d'étendre l'homéomorphie de deux figures à leurs voisinages", C.R. Acad. Sci. Paris, 171: 661
• Fox, Ralph H.; Harrold, O. G. (1962), "The Wilder arcs", Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice Hall, pp. 184–187, MR 0140096
• Fox, Ralph H.; Artin, Emil (1948), "Some wild cells and spheres in three-dimensional space", Annals of Mathematics. Second Series, 49: 979–990, ISSN 0003-486X, JSTOR 1969408, MR 0027512
• Hocking, John Gilbert; Young, Gail Sellers (1988) [1961]. Topology. Dover. pp. 176–177. ISBN 0-486-65676-4. {{cite book}}: Invalid |ref=harv (help)
• McPherson, James M. (1973), "Wild arcs in three-space. I. Families of Fox–Artin arcs", Pacific Journal of Mathematics, 45: 585–598, doi:10.2140/pjm.1973.45.585, ISSN 0030-8730, MR 0343276