Icositruncated dodecadodecahedron
Appearance
| Icositruncated dodecadodecahedron | |
|---|---|
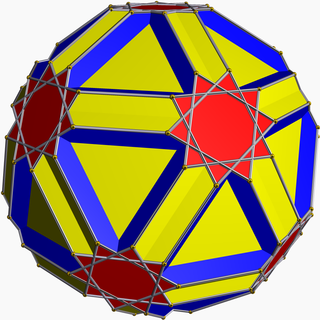
| |
| Type | Uniform star polyhedron |
| Elements | F = 44, E = 180 V = 120 (χ = −16) |
| Faces by sides | 20{6}+12{10}+12{10/3} |
| Coxeter diagram | |
| Wythoff symbol | 3 5 5/3 | |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U45, C57, W84 |
| Dual polyhedron | Tridyakis icosahedron |
| Vertex figure |  6.10.10/3 |
| Bowers acronym | Idtid |

In geometry, the icositruncated dodecadodecahedron or icosidodecatruncated icosidodecahedron is a nonconvex uniform polyhedron, indexed as U45.
Convex hull
[edit]Its convex hull is a nonuniform truncated icosidodecahedron.
 Truncated icosidodecahedron |
 Convex hull |
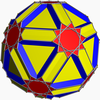 Icositruncated dodecadodecahedron |
Cartesian coordinates
[edit]Cartesian coordinates for the vertices of an icositruncated dodecadodecahedron are all the even permutations of
where is the golden ratio.
Related polyhedra
[edit]Tridyakis icosahedron
[edit]| Tridyakis icosahedron | |
|---|---|

| |
| Type | Star polyhedron |
| Face | 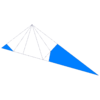
|
| Elements | F = 120, E = 180 V = 44 (χ = −16) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU45 |
| dual polyhedron | Icositruncated dodecadodecahedron |
The tridyakis icosahedron is the dual polyhedron of the icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.
See also
[edit]- Catalan solid Duals to convex uniform polyhedra
- Uniform polyhedra
- List of uniform polyhedra
References
[edit]- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208 Photo on page 96, Dorman Luke construction and stellation pattern on page 97.
External links
[edit]

![{\displaystyle {\begin{array}{crrlc}{\Bigl (}&\pm {\bigl [}2-{\frac {1}{\varphi }}{\bigr ]},&\pm \,1,&\pm {\bigl [}2+\varphi {\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,1,&\pm \,{\frac {1}{\varphi ^{2}}},&\pm {\bigl [}3\varphi -1{\bigr ]}&{\Bigr )},\\{\Bigl (}&\pm \,2,&\pm \,{\frac {2}{\varphi }},&\pm \,2\varphi &{\Bigr )},\\{\Bigl (}&\pm \,3,&\pm \,{\frac {1}{\varphi ^{2}}},&\pm \,\varphi ^{2}&{\Bigr )},\\{\Bigl (}&\pm \,\varphi ^{2},&\pm \,1,&\pm {\bigl [}3\varphi -2{\bigr ]}&{\Bigr )},\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc946dd2ad1cf9490fbc40f2b13dd9958049b453)
