Schwarz lantern

Schwarz lantern on display in the German Museum of Technology Berlin.

In mathematics, the Schwarz lantern is a polyhedral approximation to a cylinder, used as a pathological example of the difficulty of defining the area of a smooth (curved) surface as the limit of the areas of polyhedra. It is formed by stacked rings of isosceles triangles, arranged in each ring in the same pattern as an antiprism. The resulting shape can be folded from paper, and is named for mathematician Hermann Schwarz and for its resemblance to a cylindrical paper lantern. It is also known as Schwarz's boot.

As Schwarz showed, it is not sufficient to simply increase the number of rings and the number of isosceles triangles per ring, if the surface area of the polyhedron is to converge to the surface area of the curved surface. Depending on the relation of the number of rings to the number of triangles per ring, the area of the lantern can converge to the area of the cylinder, to a limit arbitrarily larger than the area of the cylinder, to infinity or in other words to diverge. Thus, the Schwarz lantern demonstrates that, to approximate the area of a curved surface, sampling the surface by close-together points and connecting them by triangles of small diameter is inadequate to ensure an accurate approximation. The phenomenon in which closely sampled points on a smooth surface can lead to polyhedral approximations of arbitrarily large area has been called the Schwarz paradox.

History and motivation

In the work of Archimedes it already appears that the length of a circle can be approximated by the length of regular polyhedra inscribed or circumscribed in the circle. In general, for smooth or rectifiable curves their length can be defined as the supremum of the lengths of polygonal curves inscribed in them. The Schwarz lantern shows that surface area cannot be defined as the supremum of inscribed polyhedral surfaces.

The Schwarz lantern is named for Hermann Schwarz

German mathematician Hermann Schwarz (1843–1921) devised his construction in the late 19th century as a counterexample to the erroneous definition in J. A. Serret's 1868 book Cours de calcul differentiel et integral, which incorrectly states that:

Soit une portion de surface courbe terminée par un contour $C$; nous nommerons aire de cette surface la limite $S$ vers laquelle tend l'aire d'une surface polyédrale inscrite formée de faces triangulaires et terminee par un contour polygonal $\Gamma$ ayant pour limite le contour $C$.

Il faut démontrer que la limite $S$ existe et qu'elle est indépendante de la loi suivant laquelle décroissent les faces de la surface polyedrale inscrite.

In English:

Let a portion of curved surface be bounded by a contour $C$; we will define the area of this surface to be the limit $S$ tended towards by the area of an inscribed polyhedral surface formed from triangular faces and bounded by a polygonal contour $\Gamma$ whose limit is the contour $C$.

It must be shown that the limit $S$ exists and that it is independent of the law according to which the faces of the inscribed polyhedral surface shrink.

Independently of Schwarz, Giuseppe Peano found the same counterexample. At the time, Peano was a student of Angelo Genocchi, who already knew about the difficulty of defining surface area from communication with Schwarz. Genocchi informed Charles Hermite, who had been using Serret's erroneous definition in his course. Hermite asked Schwarz for details, revised his course, and published the example in the second edition of his lecture notes (1883). The original note from Schwarz to Hermite was not published until the second edition of Schwarz's collected works in 1890.

As well as continuing to serve as an instructive example of the need for careful definitions in calculus, the Schwarz paradox is important for the finite element method for scientific and engineering simulations. Basic forms of this method involve approximating smooth functions on the plane by piecewise-linear functions on triangulations of the plane, and for the Schwarz lantern this approximation can converge to the wrong value. Its incorrect result can be attributed to the possibility that its triangles have angles arbitrarily close to 180°. In contrast, Schwarz lanterns whose angles are bounded away from 180° accurately approximate the cylinder area. This phenomenon has been used to motivate mesh generation methods for which all angles are bounded away from 180°, such as nonobtuse meshes.

Construction

The discrete polyhedral approximation considered by Schwarz can be described by two parameters, $m$ and $n$. The cylinder is sliced by parallel planes into $m$ shorter cylinders, bounded by $m+1$ circles: two circles at the ends of the starting cylinder, and $m-1$ more cylinders in each of the slicing planes. Each of these circles contains $n$ vertices of the Schwarz lantern, spaced equally along the circle. The resulting regular polygons in each circle are rotated by an angle of $\pi /n$ with respect to each other, so that each vertex on one circle is placed near to the arc midpoints of the adjacent circles. From these vertices, the Schwarz lantern is defined as a polyhedral surface formed from isosceles triangles. Each triangle has as its base two consecutive vertices along one of the circular slices, and as its apex a vertex from an adjacent cycle. These triangles meet edge-to-edge to form a polyhedral manifold, topologically equivalent to the cylinder that is being approximated.

Origami crease pattern for a Schwarz lantern with $m=16$ and $n=4$

Each interior vertex touches two apex angles and four base angles of congruent isosceles triangles, adding to a total angle of $2\pi$, the same as it would in a tessellation of a flat plane by triangles of the same shape. As a consequence, the Schwarz lantern can be folded out of a flat piece of paper, although the resulting surface will have a seam rather than forming a continuous cylinder. The crease pattern for this folded surface is the tessellation of the paper by isosceles triangles. This crease pattern has also been called the Yoshimura pattern, after the work of Y. Yoshimura on the Yoshimura buckling pattern of cylindrical surfaces under axial compression, which can be similar in shape to the Schwarz lantern.

Area

The area of the Schwarz lantern, for any particular choice of the parameters $m$ and $n$, can be calculated by a straightforward application of trigonometry. A straight circular cylinder of radius $r$ and length $\ell$ has area $2\pi r\ell$. For a Schwarz lantern with parameters $m$ and $n$, each band is a shorter cylinder of length $\ell /m$, approximated by $2n$ isosceles triangles. The length of the base of each triangle can be found from the formula for the edge length of a regular $n$-gon, as

$$2r\sin {\frac {\pi }{n}}.$$

The height $h$ of each triangle can be found by applying the Pythagorean theorem to a right triangle formed by the apex of the triangle, the midpoint of the base, and the midpoint of the arc of the circle bounded by the endpoints of the base. The two sides of this right triangle are the length $\ell /m$ of the cylindrical band, and the sagitta of the arc, giving the formula

$$h^{2}=\left({\frac {\ell }{m}}\right)^{2}+\left(r\left(1-\cos {\frac {\pi }{n}}\right)\right)^{2}.$$

Combining the formula for the area of each triangle from its base and height, and the total number $2mn$ of the triangles, gives the Schwarz lantern a total area of

$$A(m,n)=2mn\left(r\sin {\frac {\pi }{n}}\right){\sqrt {\left({\frac {\ell }{m}}\right)^{2}+r^{2}\left(1-\cos {\frac {\pi }{n}}\right)^{2}}}.$$

Limits

Animation of Schwarz lantern convergence (or lack thereof) for various relations between its two parameters

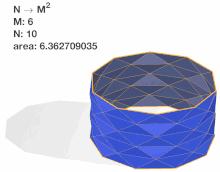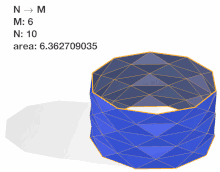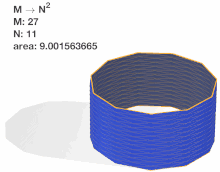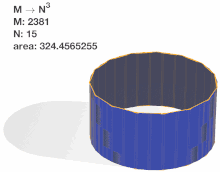
Because there are two free parameters $m$ and $n$, the limiting area of the Schwarz lantern, as both $m$ and $n$ become arbitrarily large, can be evaluated in different orders, with different results. If $m$ is fixed while $n$ grows, and the resulting limit is then evaluated for arbitrarily large choices of $m$, one obtains

$$\lim _{m\to \infty }\lim _{n\to \infty }A(m,n)=2\pi r\ell ,$$

the correct area for the cylinder. In this case, the inner limit already converges to the same value, and the outer limit is superfluous. Geometrically, substituting each cylindrical band by a band of very sharp isosceles triangles accurately approximates its area.

On the other hand, reversing the ordering of the limits gives

$$\lim _{n\to \infty }\lim _{m\to \infty }A(m,n)=\infty .$$

In this case, for a fixed choice of $n$, as $m$ grows and the length $\ell /m$ of each cylindrical band becomes arbitrarily small, each corresponding band of isosceles triangles becomes nearly planar. Each triangle approaches the triangle formed by two consecutive edges of a regular $2n$-gon, and the area of the whole band of triangles approaches $2n$ times the area of one of these planar triangles, a finite number. However, the number $m$ of these bands grows arbitrarily large. Therefore, the area of the Schwarz lantern grows in approximate proportion to $m$, itself becoming arbitrarily large.

It is also possible to fix a functional relation between $m$ and $n$, and to examine the limit as both parameters grow large simultaneously, maintaining this relation. Different choices of this relation can lead to either of the two behaviors described above, convergence to the correct area or divergence to infinity. For instance, setting $m=cn$ (for an arbitrary constant $c$) and taking the limit for large $n$ leads to convergence to the correct area, while setting $m=cn^{3}$ leads to divergence. A third type of limiting behavior is obtained by setting $m=cn^{2}$. For this choice,

$$\lim _{n\to \infty }A(cn^{2},n)=2\pi r{\sqrt {\ell ^{2}+{\frac {r^{2}\pi ^{4}c^{2}}{4}}}}.$$

In this case, the area of the Schwarz lantern, parameterized in this way, converges, but it converges to a larger value than the area of the cylinder it is inscribed into. Any desired larger area can be obtained by making an appropriate choice of the constant $c$.

See also

• Runge's phenomenon, another example of failure of convergence

External links

• Bogomolny, Alexander. "The Schwarz Lantern Explained". Cut-the-knot.
• Marx, Jean-Pierre (September 17, 2016). "The Schwarz Lantern". Math Counterexamples.
• Lamb, Evelyn (November 30, 2013). "Counterexamples in origami". Roots of unity. Scientific American.