Triaugmented triangular prism: Difference between revisions
vandalism |
merge from Fritsch graph and copyedit |
||
| Line 13: | Line 13: | ||
}} |
}} |
||
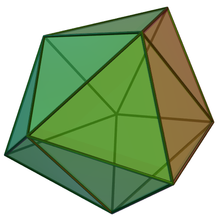
In [[geometry]], the '''triaugmented triangular prism''', '''tetracaidecadeltahedron''', or '''tetrakis triangular prism''' is |
In [[geometry]], the '''triaugmented triangular prism''', '''tetracaidecadeltahedron''', or '''tetrakis triangular prism''' is a [[convex polyhedron]] with 14 [[equilateral triangle]]s as its faces. It is a [[deltahedron]] (a convex polyhedron with equilateral triangle faces) and a [[Johnson solid]] (a convex polyhedron with regular faces, <math>J_{51}</math>). It can be constructed by attaching [[equilateral square pyramid]]s to each of the three square faces of a [[triangular prism]]. |
||
The graph of the triaugmented triangular prism, a [[maximal planar graph]] with 9 vertices and 21 edges, has been called the '''Fritsch graph'''. The [[dual polyhedron]] of the the triaugmented triangular prism is an [[associahedron]]. |
|||
{{Johnson solid}} |
|||
==Area and volume== |
|||
A triaugmented triangular prism with edge length <math>a</math> has surface area |
|||
<math display=block>\frac{7\sqrt{3}}{2}a^2,</math> |
|||
the area of 14 equilateral triangles. Its volume |
|||
<math display=block>\frac{2\sqrt{2}+\sqrt{3}}{4}a^3,</math> |
|||
can be derived by partitioning it into a central prism and three square pyramids, and summing their volumes. |
|||
== Fritsch graph == |
|||
The graph of the triaugmented triangular prism has 9 vertices and 21 edges. It was used by {{harvtxt|Fritsch|Fritsch|1998}} as a small counterexample to [[Alfred Kempe]]'s false proof of the [[four color theorem]] using [[Kempe chain]]s, and its dual graph (the graph of the [[associahedron]]) is used as the cover illustration to {{harvtxt|Fritsch|Fritsch|1998}}.{{r|ff98}} Because of this usage, this graph has subsequently been named the '''Fritsch graph'''.{{r|involve}} |
|||
== Dual polyhedron == |
== Dual polyhedron == |
||
| Line 21: | Line 31: | ||
The [[Dual polyhedron|dual]] of the triaugmented triangular prism is an '''order-4 truncated triangular bipyramid''', also known as an order-5 [[associahedron]]. This transparent image shows its three [[Square (geometry)|square]], and six congruent irregular [[pentagon]]al [[Face (geometry)|face]]s. [[Edge (geometry)|Edges]] are colored to distinguish the 3 different edge lengths. |
The [[Dual polyhedron|dual]] of the triaugmented triangular prism is an '''order-4 truncated triangular bipyramid''', also known as an order-5 [[associahedron]]. This transparent image shows its three [[Square (geometry)|square]], and six congruent irregular [[pentagon]]al [[Face (geometry)|face]]s. [[Edge (geometry)|Edges]] are colored to distinguish the 3 different edge lengths. |
||
== |
==References== |
||
{{reflist|refs= |
|||
For edge length ''a'', the surface area is <math>\frac{7\sqrt{3}}{2}a^2</math> and the volume is <math>\frac{2\sqrt{2}+\sqrt{3}}{4}a^3</math>, derivable by summing up the respective contributions from the prism and the pyramids. |
|||
<ref name=involve>{{citation |
|||
| last1 = Gethner | first1 = Ellen | author1-link = Ellen Gethner |
|||
| last2 = Kallichanda | first2 = Bopanna |
|||
| last3 = Mentis | first3 = Alexander |
|||
| last4 = Braudrick | first4 = Sarah |
|||
| last5 = Chawla | first5 = Sumeet |
|||
| last6 = Clune | first6 = Andrew |
|||
| last7 = Drummond | first7 = Rachel |
|||
| last8 = Evans | first8 = Panagiota |
|||
| last9 = Roche | first9 = William |
|||
| last10 = Takano | first10 = Nao |
|||
| date = October 2009 |
|||
| doi = 10.2140/involve.2009.2.249 |
|||
| issue = 3 |
|||
| journal = Involve, a Journal of Mathematics |
|||
| pages = 249–265 |
|||
| publisher = Mathematical Sciences Publishers |
|||
| title = How false is Kempe's proof of the Four Color Theorem? Part II |
|||
| volume = 2}}</ref> |
|||
<ref name=ff98>{{citation |
|||
| last1 = Fritsch | first1 = Rudolf |
|||
| last2 = Fritsch | first2 = Gerda |
|||
| doi = 10.1007/978-1-4612-1720-6 |
|||
| isbn = 0-387-98497-6 |
|||
| location = New York |
|||
| mr = 1633950 |
|||
| publisher = Springer-Verlag |
|||
| title = The Four-Color Theorem: History, Topological Foundations, and Idea of Proof |
|||
| year = 1998}}</ref> |
|||
}} |
|||
==External links== |
==External links== |
||
* {{MathWorld | urlname=TriaugmentedTriangularPrism | title= Triaugmented triangular prism }} |
* {{MathWorld | urlname=TriaugmentedTriangularPrism | title= Triaugmented triangular prism |mode=cs2}} |
||
[[Category:Johnson solids]] |
[[Category:Johnson solids]] |
||
Revision as of 01:26, 26 September 2022
| Triaugmented triangular prism | |
|---|---|
 | |
| Type | Deltahedron, Johnson J50 – J51 – J52 |
| Faces | 14 (2+2×6) triangles |
| Edges | 21 |
| Vertices | 9 |
| Vertex configuration | 3(34) 6(35) |
| Symmetry group | D3h |
| Dual polyhedron | Order-4 truncated triangular bipyramid (associahedron K5) |
| Properties | convex |
| Net | |
 | |
In geometry, the triaugmented triangular prism, tetracaidecadeltahedron, or tetrakis triangular prism is a convex polyhedron with 14 equilateral triangles as its faces. It is a deltahedron (a convex polyhedron with equilateral triangle faces) and a Johnson solid (a convex polyhedron with regular faces, ). It can be constructed by attaching equilateral square pyramids to each of the three square faces of a triangular prism.
The graph of the triaugmented triangular prism, a maximal planar graph with 9 vertices and 21 edges, has been called the Fritsch graph. The dual polyhedron of the the triaugmented triangular prism is an associahedron.
Area and volume
A triaugmented triangular prism with edge length has surface area
Fritsch graph
The graph of the triaugmented triangular prism has 9 vertices and 21 edges. It was used by Fritsch & Fritsch (1998) as a small counterexample to Alfred Kempe's false proof of the four color theorem using Kempe chains, and its dual graph (the graph of the associahedron) is used as the cover illustration to Fritsch & Fritsch (1998).[1] Because of this usage, this graph has subsequently been named the Fritsch graph.[2]
Dual polyhedron
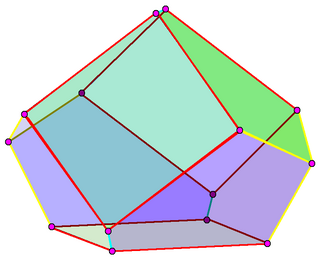
The dual of the triaugmented triangular prism is an order-4 truncated triangular bipyramid, also known as an order-5 associahedron. This transparent image shows its three square, and six congruent irregular pentagonal faces. Edges are colored to distinguish the 3 different edge lengths.
References
- ^ Fritsch, Rudolf; Fritsch, Gerda (1998), The Four-Color Theorem: History, Topological Foundations, and Idea of Proof, New York: Springer-Verlag, doi:10.1007/978-1-4612-1720-6, ISBN 0-387-98497-6, MR 1633950
- ^ Gethner, Ellen; Kallichanda, Bopanna; Mentis, Alexander; Braudrick, Sarah; Chawla, Sumeet; Clune, Andrew; Drummond, Rachel; Evans, Panagiota; Roche, William; Takano, Nao (October 2009), "How false is Kempe's proof of the Four Color Theorem? Part II", Involve, a Journal of Mathematics, 2 (3), Mathematical Sciences Publishers: 249–265, doi:10.2140/involve.2009.2.249




