Snub disphenoid: Difference between revisions
move convex |
Dedhert.Jr (talk | contribs) rewrite the article, refactor the sections, pulls ref for readibility, add facts and more sources (probably needs provide more than ever), remove wolfram source and fact (per talk), mathfying, and other changes |
||
| Line 1: | Line 1: | ||
{{short description| |
{{short description|Convex polyhedron with 12 triangular faces}} |
||
{{Infobox polyhedron |
{{Infobox polyhedron |
||
|image=snub_disphenoid.png |
|image=snub_disphenoid.png |
||
| Line 12: | Line 12: | ||
|net=Johnson_solid_84_net.png |
|net=Johnson_solid_84_net.png |
||
}} |
}} |
||
[[File:J84 snub disphenoid.stl|thumb|3D model of a snub disphenoid]] |
|||
In [[geometry]], the '''snub disphenoid |
In [[geometry]], the '''snub disphenoid''' is a [[convex polyhedron]] with 12 [[equilateral triangle]]s as its [[face (geometry)|faces]]. It is an example of [[deltahedron]] and [[Johnson solid]]. It can be constructed in different approaches. This shape also has alternative names called '''Siamese dodecahedron''', '''triangular dodecahedron''', '''trigonal dodecahedron''', or '''dodecadeltahedron'''; these names mean the 12-sided polyhedron. |
||
The applications of snub disphenoid can be visualized as an [[atom cluster]] surrounding a central atom, that is the [[dodecahedral molecular geometry]]. Its vertices may be placed in a sphere and can also be used as a minimum possible [[Lennard-Jones potential]] among all eight-sphere clusters. The dual polyhedron of the snub disphenoid is the [[elongated gyrobifastigium]]. |
|||
The snub disphenoid is also the vertex figure of the [[Isogonal figure|isogonal]] 13-5 step prism, a [[polychoron]] constructed from a 13-13 [[duoprism]] by selecting a vertex on a [[tridecagon]], then selecting the 5th vertex on the next tridecagon, doing so until reaching the original tridecagon. It cannot be made uniform, however, because the snub disphenoid has no [[circumscribed sphere]]. |
|||
== Construction == |
|||
=== Involving polyhedron === |
|||
The snub disphenoid can be constructed in different ways. As suggested by the name, the snub disphenoid is constructed from [[tetragonal disphenoid]] by cutting all the edges from its faces, and adding [[equilateral triangle]]s (the light blue colors in the following image) that are twisted in a certain angle between them.{{cn|date=March 2024|reason=Missing source mentions specifically about the construction of snub disphenoid. The latter citation is about the snubification in general.}} This process construction is known as [[Snub (geometry)|snubification]].{{r|holme}} |
|||
{{multiple image |
|||
| image1 = Digonal antiprism.png |
|||
| image2 = Snub digonal antiprism.png |
|||
| footer = Process of constructing snub disphenoid by [[Snub (geometry)|snubification]] |
|||
| total_width = 400 |
|||
| align = center |
|||
}} |
|||
The snub disphenoid may also be constructed from a triangular bipyramid, by cutting its two edges along the apices. These apices can be pushed toward each other resulting in the new two vertices pushed away.{{r|hartshorne}} Alternatively, the snub disphenoid can be constructed from [[pentagonal bipyramid]] by cutting the two edges along that connecting the base of the bipyramid and then inserting two equilateral triangles between them.{{r|timofeenko}} Another way to construct the snub disphenoid is started from the [[square antiprism]], by replacing the two square faces with pairs of equilateral triangles. Another construction of the ''snub disphenoid'' is as a digonal [[gyrobianticupola]]. It has the same topology and symmetry but without equilateral triangles. It has 4 vertices in a [[square]] on a center plane as two [[anticupola]]e attached with rotational symmetry. |
|||
A physical model of the snub disphenoid can be formed by folding a [[Net (polyhedron)|net]] formed by 12 equilateral triangles (a [[polyiamond|12-iamond]]), shown. An alternative net suggested by [[John Montroll]] has fewer concave vertices on its boundary, making it more convenient for [[origami]] construction.{{r|montroll}} |
|||
=== By Cartesian coordinates === |
|||
The eight vertices of the snub disphenoid may then be given [[Cartesian coordinate]]s: |
|||
<math display="block"> \begin{align} |
|||
(\pm t, r, 0), &\qquad (0, -r, \pm t), \\ |
|||
(\pm 1, -s, 0), &\qquad (0, s, \pm 1). |
|||
\end{align} </math> |
|||
Here, <math> q \approx 0.16902 </math> is the positive real solution of [[Casus irreducibilis|the cubic polynomial]] <math display="inline"> 2x^3 +11x^2+4x-1.</math>. The three variables <math> r </math>, <math> s </math>, and <math> t </math> is the expression of:{{r|shdc}} |
|||
<math display="block"> r = \sqrt{q} \approx 0.41112, \qquad s = \sqrt{\frac{1-q}{2q}} \approx 1.56786, \qquad t = 2rs = \sqrt{2-2q} \approx 1.28917.</math> |
|||
Because this construction involves the solution to a cubic equation, the snub disphenoid cannot be [[Compass-and-straightedge construction|constructed with a compass and straightedge]], unlike the other seven deltahedra.{{r|hartshorne}} |
|||
==Properties== |
|||
As a consequence of such constructions, the snub disphenoid has 12 equilateral triangles. A [[deltahedron]] is a polyhedron in which all faces are equilateral triangles. There are eight convex deltahedra, one of which is the snub disphenoid.{{r|cundy}} More generally, the [[Convex set|convex]] polyhedron in which all faces are [[regular polygon]] are the [[Johnson solid]]s, and every convex deltahedron is Johnson solid. The snub disphenoid is among them, enumerated as the 84th Johnson solid <math> J_{84} </math>.{{r|francis}} |
|||
=== Measurement === |
|||
A snub disphenoid with edge length <math> a </math> has a surface area: |
|||
<math display="block"> 2 \left(1 + 3\sqrt{3}\right)a^2 \approx 12.392a^2, </math> |
|||
the area of 12 equilateral triangles.{{r|berman}} Its volume can be calculated by using the following formula |
|||
<math display="block"> \xi a^3 \approx \approx 0.85949 a^3. </math> |
|||
=== Symmetry and geodesic === |
|||
[[File:J84 snub disphenoid.stl|thumb|left|3D model of a snub disphenoid]] |
|||
The snub disphenoid has the same symmetries as a [[tetragonal disphenoid]], the [[Dihedral symmetry in three dimensions|antiprismatic symmetry]] <math> D_{2 \mathrm{d}} </math> of order 8: it has an axis of 180° rotational symmetry through the midpoints of its two opposite edges, two perpendicular planes of [[reflection symmetry]] through this axis, and four additional symmetry operations given by a reflection perpendicular to the axis followed by a quarter-turn and possibly another reflection parallel to the axis.{{r|cundy}}. |
|||
Up to symmetries and parallel translation, the snub disphenoid has five types of simple (non-self-crossing) [[closed geodesic]]s. These are paths on the surface of the polyhedron that avoid the vertices and locally look like the shortest path: they follow straight line segments across each face of the polyhedron that they intersect, and when they cross an edge of the polyhedron they make complementary angles on the two incident faces to the edge. Intuitively, one could stretch a rubber band around the polyhedron along this path and it would stay in place: there is no way to locally change the path and make it shorter. For example, one type of geodesic crosses the two opposite edges of the snub disphenoid at their midpoints (where the symmetry axis exits the polytope) at an angle of <math> \pi/3 </math>. A second type of geodesic passes near the intersection of the snub disphenoid with the plane that perpendicularly bisects the symmetry axis (the [[equator]] of the polyhedron), crossing the edges of eight triangles at angles that alternate between <math> \pi/2 </math> and <math> \pi/6 </math>. Shifting a geodesic on the surface of the polyhedron by a small amount (small enough that the shift does not cause it to cross any vertices) preserves the property of being a geodesic and preserves its length, so both of these examples have shifted versions of the same type that are less symmetrically placed. The lengths of the five simple closed geodesics on a snub disphenoid with unit-length edges are |
|||
:<math>2\sqrt{3}\approx 3.464</math> (for the equatorial geodesic), <math>\sqrt{13}\approx 3.606</math>, <math>4</math> (for the geodesic through the midpoints of opposite edges), <math>2\sqrt{7}\approx 5.292</math>, and <math>\sqrt{19}\approx 4.359</math>. |
|||
Except for the tetrahedron, which has infinitely many types of simple closed geodesics, the snub disphenoid has the most types of geodesics of any deltahedron.{{r|lptw}} |
|||
=== Representation by the graph === |
|||
The snub disphenoid is [[k-vertex-connected graph|4-connected]], meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected [[simplicial polytope|simplicial]] [[well-covered graph|well-covered]] polyhedra, meaning that all of the [[maximal independent set]]s of its vertices have the same size. The other three polyhedra with this property are the [[regular octahedron]], the [[pentagonal bipyramid]], and an irregular polyhedron with 12 vertices and 20 triangular faces.{{r|fhnp}} |
|||
== Dual polyhedron == |
|||
[[File:Dual digonal gyrobianticupola.png|240px|thumb|right|The dual polyhedron of elongated gyrobifastigium]] |
|||
The dual polyhedron of the snub disphenoid is the [[elongated gyrobifastigium]]. It has right-angled pentagons and can self-tessellate space. |
|||
== Applications == |
|||
Spheres centered at the vertices of the snub disphenoid form a cluster that, according to numerical experiments, has the minimum possible [[Lennard-Jones potential]] among all eight-sphere clusters.{{r|shdc}} |
|||
In the geometry of [[chemical compound]]s, a polyhedron may be visualized as the [[atom cluster]] surrounding a central atom. The [[dodecahedral molecular geometry]] describes the cluster for which it is a snub disphenoid.{{r|bhf}} |
|||
==History and naming== |
==History and naming== |
||
This shape was called a ''Siamese dodecahedron'' in the paper by [[Hans Freudenthal]] and [[Bartel Leendert van der Waerden|B. L. van der Waerden]] (1947) which first described the set of eight convex [[Deltahedron|deltahedra]]. |
This shape was called a ''Siamese dodecahedron'' in the paper by [[Hans Freudenthal]] and [[Bartel Leendert van der Waerden|B. L. van der Waerden]] (1947) which first described the set of eight convex [[Deltahedron|deltahedra]].{{r|fw}} |
||
| last1 = Freudenthal | first1 = H. | author1-link = Hans Freudenthal |
|||
The ''dodecadeltahedron'' name was given to the same shape by {{harvtxt|Bernal|1964}}, referring to the fact that it is a 12-sided deltahedron. There are other [[simplicial polyhedron|simplicial dodecahedra]], such as the [[hexagonal bipyramid]], but this is the only one that can be realized with equilateral faces. Bernal was interested in the shapes of holes left in irregular close-packed arrangements of spheres, so he used a restrictive definition of deltahedra, in which a deltahedron is a convex polyhedron with triangular faces that can be formed by the centers of a collection of congruent spheres, whose tangencies represent polyhedron edges, and such that there is no room to pack another sphere inside the cage created by this system of spheres. This restrictive definition disallows the [[triangular bipyramid]] (as forming two tetrahedral holes rather than a single hole), [[pentagonal bipyramid]] (because the spheres for its apexes interpenetrate, so it cannot occur in sphere packings), and [[icosahedron]] (because it has interior room for another sphere). Bernal writes that the snub disphenoid is "a very common [[Coordination geometry|coordination]] for the [[calcium ion]] in [[crystallography]]".{{r|bernal}} In coordination geometry, it is usually known as the trigonal dodecahedron or simply as the dodecahedron.{{r|hartshorne}}{{cn|date=March 2024|reason=Cannot find the source for the alternative name, dodecahedron.}} |
|||
| last2 = van d. Waerden | first2 = B. L. | author2-link = Bartel Leendert van der Waerden |
|||
| journal = [[Simon Stevin (journal)|Simon Stevin]] |
|||
The ''snub disphenoid'' name comes from [[Norman Johnson (mathematician)|Norman Johnson]]'s 1966 classification of the [[Johnson solid]]s, convex polyhedra all of whose faces are regular.{{r|johnson}} It exists first in a series of polyhedra with axial symmetry, so also can be given the name ''digonal [[gyrobianticupola]]''. |
|||
| mr = 0021687 |
|||
| pages = 115–121 |
|||
== References == |
|||
| title = On an assertion of Euclid |
|||
{{reflist|refs= |
|||
| volume = 25 |
|||
| year = 1947}}.</ref> The ''dodecadeltahedron'' name was given to the same shape by {{harvtxt|Bernal|1964}}, referring to the fact that it is a 12-sided deltahedron. There are other [[simplicial polyhedron|simplicial dodecahedra]], such as the [[hexagonal bipyramid]], but this is the only one that can be realized with equilateral faces. Bernal was interested in the shapes of holes left in irregular close-packed arrangements of spheres, so he used a restrictive definition of deltahedra, in which a deltahedron is a convex polyhedron with triangular faces that can be formed by the centers of a collection of congruent spheres, whose tangencies represent polyhedron edges, and such that there is no room to pack another sphere inside the cage created by this system of spheres. This restrictive definition disallows the [[triangular bipyramid]] (as forming two tetrahedral holes rather than a single hole), [[pentagonal bipyramid]] (because the spheres for its apexes interpenetrate, so it cannot occur in sphere packings), and [[icosahedron]] (because it has interior room for another sphere). Bernal writes that the snub disphenoid is "a very common [[Coordination geometry|coordination]] for the [[calcium ion]] in [[crystallography]]".<ref>{{citation |
|||
<ref name="berman">{{citation |
|||
| last = Berman | first = Martin |
|||
| doi = 10.1016/0016-0032(71)90071-8 |
|||
| journal = Journal of the Franklin Institute |
|||
| mr = 290245 |
|||
| pages = 329–352 |
|||
| title = Regular-faced convex polyhedra |
|||
| volume = 291 |
|||
| year = 1971| issue = 5 |
|||
}}.</ref> |
|||
<ref name="bernal">{{citation |
|||
| last = Bernal | first = J. D. | author-link = John Desmond Bernal |
| last = Bernal | first = J. D. | author-link = John Desmond Bernal |
||
| issue = 1382 |
| issue = 1382 |
||
| Line 35: | Line 101: | ||
| title = The Bakerian Lecture, 1962. The Structure of Liquids |
| title = The Bakerian Lecture, 1962. The Structure of Liquids |
||
| volume = 280 |
| volume = 280 |
||
| year = 1964| doi = 10.1098/rspa.1964.0147 | bibcode = 1964RSPSA.280..299B | s2cid = 178710030 |
| year = 1964| doi = 10.1098/rspa.1964.0147 | bibcode = 1964RSPSA.280..299B | s2cid = 178710030 |
||
}}.</ref> |
|||
<ref name="bhf">{{citation |
|||
The ''snub disphenoid'' name comes from [[Norman Johnson (mathematician)|Norman Johnson]]'s 1966 classification of the [[Johnson solid]]s, convex polyhedra all of whose faces are regular.<ref>{{citation |
|||
| last1 = Burdett | first1 = Jeremy K. |
|||
| last = Johnson | first = Norman W. | author-link = Norman Johnson (mathematician) |
|||
| last2 = Hoffmann | first2 = Roald |
|||
| doi = 10.4153/cjm-1966-021-8 |
|||
| last3 = Fay | first3 = Robert C. |
|||
| journal = [[Canadian Journal of Mathematics]] |
|||
| |
| title = Eight-Coordination |
||
| journal = [[Inorganic Chemistry (journal)|Inorganic Chemistry]] |
|||
| pages = 169–200 |
|||
| year = 1978 |
|||
| title = Convex polyhedra with regular faces |
|||
| volume = |
| volume = 17 | issue = 9 | pages = 2553–2568 |
||
| |
| doi = 10.1021/ic50187a041 |
||
}}.</ref> |
|||
| zbl = 0132.14603 | s2cid = 122006114 | doi-access = free |
|||
}}.</ref> It exists first in a series of polyhedra with axial symmetry, so also can be given the name ''digonal [[gyrobianticupola]]''. |
|||
<ref name="cundy">{{citation |
|||
==Properties== |
|||
| last = Cundy | first = H. Martyn | author-link = Martyn Cundy |
|||
The snub disphenoid is [[k-vertex-connected graph|4-connected]], meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected [[simplicial polytope|simplicial]] [[well-covered graph|well-covered]] polyhedra, meaning that all of the [[maximal independent set]]s of its vertices have the same size. The other three polyhedra with this property are the [[regular octahedron]], the [[pentagonal bipyramid]], and an irregular polyhedron with 12 vertices and 20 triangular faces.<ref>{{citation |
|||
| doi = 10.2307/3608204 |
|||
| journal = [[The Mathematical Gazette]] |
|||
| mr = 0051525 |
|||
| pages = 263–266 |
|||
| title = Deltahedra |
|||
| volume = 36 |
|||
| year = 1952| issue = 318 | jstor = 3608204 | s2cid = 250435684 |
|||
}}.</ref> |
|||
<ref name="fhnp">{{citation |
|||
| last1 = Finbow | first1 = Arthur S. |
| last1 = Finbow | first1 = Arthur S. |
||
| last2 = Hartnell | first2 = Bert L. |
| last2 = Hartnell | first2 = Bert L. |
||
| Line 65: | Line 141: | ||
}}.</ref> |
}}.</ref> |
||
<ref name="francis">{{citation |
|||
The snub disphenoid has the same symmetries as a [[tetragonal disphenoid]]: it has an axis of 180° rotational symmetry through the midpoints of its two opposite edges, two perpendicular planes of [[reflection symmetry]] through this axis, and four additional symmetry operations given by a reflection perpendicular to the axis followed by a quarter-turn and possibly another reflection parallel to the axis.<ref>{{citation |
|||
| last = |
| last = Francis | first = Darryl |
||
| title = Johnson solids & their acronyms |
|||
| doi = 10.2307/3608204 |
|||
| journal = |
| journal = Word Ways |
||
| |
| date = August 2013 |
||
| volume = 46 | issue = 3 | page = 177 |
|||
| pages = 263–266 |
|||
| url = https://go.gale.com/ps/i.do?id=GALE%7CA340298118 |
|||
| title = Deltahedra |
|||
}}</ref> |
|||
| volume = 36 |
|||
| year = 1952| issue = 318 | jstor = 3608204 | s2cid = 250435684 }}.</ref> That is, it has {{math|''D''<sub>2''d''</sub>}} [[Dihedral symmetry in three dimensions|antiprismatic symmetry]], a symmetry group of order 8. |
|||
<ref name="fw">{{citation |
|||
Spheres centered at the vertices of the snub disphenoid form a cluster that, according to numerical experiments, has the minimum possible [[Lennard-Jones potential]] among all eight-sphere clusters.<ref name="shdc">{{citation|last1=Sloane|first1=N. J. A.|title=Minimal-energy clusters of hard spheres|journal=[[Discrete and Computational Geometry]]|volume=14|issue=3|pages=237–259|year=1995|doi=10.1007/BF02570704|mr=1344734|last2=Hardin|first2=R. H.|last3=Duff|first3=T. D. S.|last4=Conway|first4=J. H.|author1-link=Neil Sloane|author4-link=John Horton Conway|doi-access=free}}.</ref> |
|||
| last1 = Freudenthal | first1 = H. | author1-link = Hans Freudenthal |
|||
| last2 = van d. Waerden | first2 = B. L. | author2-link = Bartel Leendert van der Waerden |
|||
| journal = [[Simon Stevin (journal)|Simon Stevin]] |
|||
| mr = 0021687 |
|||
| pages = 115–121 |
|||
| title = On an assertion of Euclid |
|||
| volume = 25 |
|||
| year = 1947}}.</ref> |
|||
<ref name="hartshorne">{{citation |
|||
Up to symmetries and parallel translation, the snub disphenoid has five types of simple (non-self-crossing) [[closed geodesic]]s. These are paths on the surface of the polyhedron that avoid the vertices and locally look like a shortest path: they follow straight line segments across each face of the polyhedron that they intersect, and when they cross an edge of the polyhedron they make complementary angles on the two incident faces to the edge. Intuitively, one could stretch a rubber band around the polyhedron along this path and it would stay in place: there is no way to locally change the path and make it shorter. For example, one type of geodesic crosses the two opposite edges of the snub disphenoid at their midpoints (where the symmetry axis exits the polytope) at an angle of {{pi}}/3. A second type of geodesic passes near the intersection of the snub disphenoid with the plane that perpendicularly bisects the symmetry axis (the [[equator]] of the polyhedron), crossing the edges of eight triangles at angles that alternate between {{pi}}/2 and {{pi}}/6. Shifting a geodesic on the surface of the polyhedron by a small amount (small enough that the shift does not cause it to cross any vertices) preserves the property of being a geodesic and preserves its length, so both of these examples have shifted versions of the same type that are less symmetrically placed. The lengths of the five simple closed geodesics on a snub disphenoid with unit-length edges are |
|||
| last = Hartshorne | first = Robin | author-link = Robin Hartshorne |
|||
:<math>2\sqrt{3}\approx 3.464</math> (for the equatorial geodesic), <math>\sqrt{13}\approx 3.606</math>, <math>4</math> (for the geodesic through the midpoints of opposite edges), <math>2\sqrt{7}\approx 5.292</math>, and <math>\sqrt{19}\approx 4.359</math>. |
|||
| year = 2000 |
|||
Except for the tetrahedron, which has infinitely many types of simple closed geodesics, the snub disphenoid has the most types of geodesics of any deltahedron.<ref>{{citation |
|||
| title = Geometry: Euclid and Beyond |
|||
| series = Undergraduate Texts in Mathematics |
|||
| publisher = Springer-Verlag |
|||
| isbn = 9780387986500 |
|||
| url = https://books.google.com/books?id=EJCSL9S6la0C&pg=PA457 |
|||
| page = 457 |
|||
}}.</ref> |
|||
<ref name="holme">{{citation |
|||
| last = Holme | first = Audun |
|||
| year = 2010 |
|||
| title = Geometry: Our Cultural Heritage |
|||
| publisher = Springer |
|||
| url = https://books.google.com/books?id=zXwQGo8jyHUC |
|||
| isbn = 978-3-642-14441-7 |
|||
| doi = 10.1007/978-3-642-14441-7 |
|||
}}.</ref> |
|||
<ref name="johnson">{{citation |
|||
| last = Johnson | first = Norman W. | author-link = Norman Johnson (mathematician) |
|||
| doi = 10.4153/cjm-1966-021-8 |
|||
| journal = [[Canadian Journal of Mathematics]] |
|||
| mr = 0185507 |
|||
| pages = 169–200 |
|||
| title = Convex polyhedra with regular faces |
|||
| volume = 18 |
|||
| year = 1966 |
|||
| zbl = 0132.14603 | s2cid = 122006114 | doi-access = free |
|||
}}.</ref> |
|||
<ref name="lptw">{{citation |
|||
| last1 = Lawson | first1 = Kyle A. |
| last1 = Lawson | first1 = Kyle A. |
||
| last2 = Parish | first2 = James L. |
| last2 = Parish | first2 = James L. |
||
| Line 95: | Line 209: | ||
}}.</ref> |
}}.</ref> |
||
<ref name="montroll">{{citation |
|||
==Construction== |
|||
| last = Montroll | first = John | author-link = John Montroll |
|||
The snub disphenoid is constructed, as its name suggests, as the [[Snub (geometry)#Coxeter.27s snubs.2C regular and quasiregular|snub]] polyhedron formed from a [[tetragonal disphenoid]], a lower symmetry form of a regular [[tetrahedron]]. |
|||
| year = 2004 |
|||
{| class=wikitable |
|||
| title = A Constellation of Origami Polyhedra|series=Dover Origami Papercraft Series |
|||
|- |
|||
| publisher = Dover Publications, Inc. |
|||
|[[File:Digonal antiprism.png|160px]] |
|||
| isbn = 9780486439587 |
|||
|[[File:Snub digonal antiprism.png|160px]] |
|||
| contribution = Dodecadeltahedron |
|||
|- |
|||
| pages = 38–40 |
|||
!Disphenoid |
|||
| contribution-url = https://books.google.com/books?id=fiL9KbK1LjoC&pg=PA38 |
|||
!Snub disphenoid |
|||
}}.</ref> |
|||
|} |
|||
The snub operation produces a single cyclic band of triangles separating two opposite edges (red in the figure) and their adjacent triangles. The [[snub antiprism]]s are analogous in having a single cyclic band of triangles, but in the snub antiprisms these bands separate two opposite faces and their adjacent triangles rather than two opposite edges. |
|||
<ref name="shdc">{{citation |
|||
The snub disphenoid can also constructed from the [[square antiprism]] by replacing the two square faces by pairs of equilateral triangles. However, it is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the [[Platonic solid|Platonic]] and [[Archimedean solid|Archimedean]] solids. |
|||
| last1 = Sloane | first1 = N. J. A. | author1-link = Neil Sloane |
|||
| last2 = Hardin | first2 = R. H. |
|||
| last3 = Duff | first3 = T. D. S. |
|||
| last4 = Conway | first4 = J. H. | author4-link = John Horton Conway |
|||
| year = 1995 |
|||
| title = Minimal-energy clusters of hard spheres |
|||
| journal = [[Discrete and Computational Geometry]] |
|||
| volume = 14 |
|||
| issue = 3 |
|||
| pages = 237–259 |
|||
| doi = 10.1007/BF02570704 |
|||
| mr = 1344734 |
|||
|doi-access=free |
|||
}}.</ref> |
|||
<ref name="timofeenko">{{citation |
|||
A physical model of the snub disphenoid can be formed by folding a [[Net (polyhedron)|net]] formed by 12 equilateral triangles (a [[polyiamond|12-iamond]]), shown. |
|||
| last = Timofeenko | first = A. V. |
|||
An alternative net suggested by [[John Montroll]] has fewer concave vertices on its boundary, making it more convenient for [[origami]] construction.<ref>{{citation|title=A Constellation of Origami Polyhedra|series=Dover Origami Papercraft Series|first=John|last=Montroll|author-link=John Montroll|publisher=Dover Publications, Inc.|year=2004|isbn=9780486439587|contribution=Dodecadeltahedron|pages=38–40|contribution-url=https://books.google.com/books?id=fiL9KbK1LjoC&pg=PA38}}.</ref> |
|||
| year = 2009 |
|||
| title = The non-Platonic and non-Archimedean noncomposite polyhedra |
|||
| journal = Journal of Mathematical Science |
|||
| volume = 162 |
|||
| issue = 5 |
|||
| pages = 725 |
|||
| doi = 10.1007/s10958-009-9655-0 |
|||
| s2cid = 120114341 |
|||
}}.</ref> |
|||
}} |
|||
==Cartesian coordinates== |
|||
Let <math>q\approx0.16902</math> be the positive real [[Casus irreducibilis|root of the cubic polynomial]] |
|||
:<math>2x^3 +11x^2+4x-1.</math> |
|||
Furthermore, let |
|||
:<math>r=\sqrt{q} \approx 0.41112,</math> |
|||
:<math>s=\sqrt{\frac{1-q}{2q}}\approx 1.56786,</math> |
|||
and |
|||
:<math>t=2rs=\sqrt{2-2q}\approx 1.28917.</math> |
|||
The eight vertices of the snub disphenoid may then be given [[Cartesian coordinate]]s |
|||
:<math>(\pm t, r, 0),\,(0, -r, \pm t),</math> |
|||
:<math>(\pm 1, -s, 0),\,(0, s, \pm 1).</math><ref name="shdc" /> |
|||
Because this construction involves the solution to a cubic equation, the snub disphenoid cannot be [[Compass-and-straightedge construction|constructed with a compass and straightedge]], unlike the other seven deltahedra.<ref>{{citation|title=Geometry: Euclid and Beyond|series=Undergraduate Texts in Mathematics|first=Robin|last=Hartshorne|author-link=Robin Hartshorne|year=2000|publisher=Springer-Verlag|isbn=9780387986500|url=https://books.google.com/books?id=EJCSL9S6la0C&pg=PA457|page=457}}.</ref> |
|||
With these coordinates, it's possible to calculate the volume of a snub disphenoid with edge length {{mvar|a}} as <math>\xi a^3</math>, where <math>\xi\approx0.85949</math>, is the positive root of the polynomial |
|||
:<math>5832x^6-1377x^4-2160x^2-4.</math><ref>{{Cite journal|last=Wolfram Research, Inc.|date=2020|title=Wolfram{{!}}Alpha Knowledgebase|location=Champaign, IL|quote=MinimalPolynomial[PolyhedronData[{"Johnson", 84}, "Volume"], x]}}</ref> |
|||
The exact form of <math> \xi </math> can be expressed as, |
|||
:<math> \xi = \frac{1}{6\sqrt{6}} \sqrt{ 17 + \sqrt[3]{155249 - 28848 i \sqrt{237}} + \sqrt[3]{155249 + 28848 i \sqrt{237}}}, </math> |
|||
:<math> \xi = \frac{1}{6\sqrt{6}} \sqrt{ 17 + 2 \sqrt{6049} \cos \left(\frac{1}{3} \tan^{-1}\left(\frac{28848\sqrt{237}}{155249}\right)\right)}, </math> |
|||
where <math> i </math> is the imaginary unit. |
|||
== Related polyhedra == |
|||
Another construction of the ''snub disphenoid'' is as a digonal [[gyrobianticupola]]. It has the same topology and symmetry, but without equilateral triangles. It has 4 vertices in a [[square]] on a center plane as two [[anticupola]]e attached with rotational symmetry. Its dual has right-angled pentagons and can self-tessellate space. |
|||
{| class=wikitable |
|||
|- align=center |
|||
|[[File:Digonal anticupola.png|240px]]<BR>Digonal [[anticupola]] |
|||
|[[File:digonal gyrobianticupola.png|240px]]<BR>Digonal gyrobianticupola |
|||
|[[File:Dual digonal gyrobianticupola.png|240px]]<BR>(Dual) [[elongated gyrobifastigium]] |
|||
|[[File:Honeycomb by dual of digonal gyrobianticupola.png|280px]]<BR>Partial tessellation |
|||
|} |
|||
== References == |
|||
{{reflist}} |
|||
==External links== |
==External links== |
||
* {{Mathworld | urlname =SnubDisphenoid| title = Snub disphenoid }} |
* {{Mathworld | urlname =SnubDisphenoid| title = Snub disphenoid }} |
||
{{Johnson solids navigator}} |
{{Johnson solids navigator}} |
||
[[Category:Johnson solids]] |
|||
[[Category:Deltahedra]] |
|||
Revision as of 13:21, 15 March 2024
| Snub disphenoid | |
|---|---|
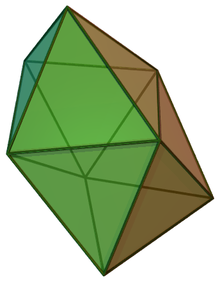 | |
| Type | Johnson J83 – J84 – J85 |
| Faces | 4+8 triangles |
| Edges | 18 |
| Vertices | 8 |
| Vertex configuration | 4(34) 4(35) |
| Symmetry group | D2d |
| Dual polyhedron | Elongated gyrobifastigium |
| Properties | convex, deltahedron |
| Net | |
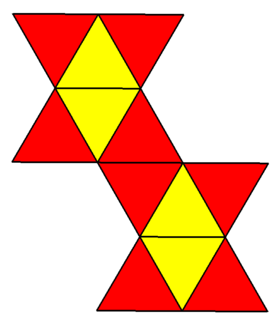 | |
In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape also has alternative names called Siamese dodecahedron, triangular dodecahedron, trigonal dodecahedron, or dodecadeltahedron; these names mean the 12-sided polyhedron.
The applications of snub disphenoid can be visualized as an atom cluster surrounding a central atom, that is the dodecahedral molecular geometry. Its vertices may be placed in a sphere and can also be used as a minimum possible Lennard-Jones potential among all eight-sphere clusters. The dual polyhedron of the snub disphenoid is the elongated gyrobifastigium.
Construction
Involving polyhedron
The snub disphenoid can be constructed in different ways. As suggested by the name, the snub disphenoid is constructed from tetragonal disphenoid by cutting all the edges from its faces, and adding equilateral triangles (the light blue colors in the following image) that are twisted in a certain angle between them.[citation needed] This process construction is known as snubification.[1]
The snub disphenoid may also be constructed from a triangular bipyramid, by cutting its two edges along the apices. These apices can be pushed toward each other resulting in the new two vertices pushed away.[2] Alternatively, the snub disphenoid can be constructed from pentagonal bipyramid by cutting the two edges along that connecting the base of the bipyramid and then inserting two equilateral triangles between them.[3] Another way to construct the snub disphenoid is started from the square antiprism, by replacing the two square faces with pairs of equilateral triangles. Another construction of the snub disphenoid is as a digonal gyrobianticupola. It has the same topology and symmetry but without equilateral triangles. It has 4 vertices in a square on a center plane as two anticupolae attached with rotational symmetry.
A physical model of the snub disphenoid can be formed by folding a net formed by 12 equilateral triangles (a 12-iamond), shown. An alternative net suggested by John Montroll has fewer concave vertices on its boundary, making it more convenient for origami construction.[4]
By Cartesian coordinates
The eight vertices of the snub disphenoid may then be given Cartesian coordinates:
Properties
As a consequence of such constructions, the snub disphenoid has 12 equilateral triangles. A deltahedron is a polyhedron in which all faces are equilateral triangles. There are eight convex deltahedra, one of which is the snub disphenoid.[6] More generally, the convex polyhedron in which all faces are regular polygon are the Johnson solids, and every convex deltahedron is Johnson solid. The snub disphenoid is among them, enumerated as the 84th Johnson solid .[7]
Measurement
A snub disphenoid with edge length has a surface area:
Symmetry and geodesic

The snub disphenoid has the same symmetries as a tetragonal disphenoid, the antiprismatic symmetry of order 8: it has an axis of 180° rotational symmetry through the midpoints of its two opposite edges, two perpendicular planes of reflection symmetry through this axis, and four additional symmetry operations given by a reflection perpendicular to the axis followed by a quarter-turn and possibly another reflection parallel to the axis.[6].
Up to symmetries and parallel translation, the snub disphenoid has five types of simple (non-self-crossing) closed geodesics. These are paths on the surface of the polyhedron that avoid the vertices and locally look like the shortest path: they follow straight line segments across each face of the polyhedron that they intersect, and when they cross an edge of the polyhedron they make complementary angles on the two incident faces to the edge. Intuitively, one could stretch a rubber band around the polyhedron along this path and it would stay in place: there is no way to locally change the path and make it shorter. For example, one type of geodesic crosses the two opposite edges of the snub disphenoid at their midpoints (where the symmetry axis exits the polytope) at an angle of . A second type of geodesic passes near the intersection of the snub disphenoid with the plane that perpendicularly bisects the symmetry axis (the equator of the polyhedron), crossing the edges of eight triangles at angles that alternate between and . Shifting a geodesic on the surface of the polyhedron by a small amount (small enough that the shift does not cause it to cross any vertices) preserves the property of being a geodesic and preserves its length, so both of these examples have shifted versions of the same type that are less symmetrically placed. The lengths of the five simple closed geodesics on a snub disphenoid with unit-length edges are
- (for the equatorial geodesic), , (for the geodesic through the midpoints of opposite edges), , and .
Except for the tetrahedron, which has infinitely many types of simple closed geodesics, the snub disphenoid has the most types of geodesics of any deltahedron.[9]
Representation by the graph
The snub disphenoid is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the regular octahedron, the pentagonal bipyramid, and an irregular polyhedron with 12 vertices and 20 triangular faces.[10]
Dual polyhedron

The dual polyhedron of the snub disphenoid is the elongated gyrobifastigium. It has right-angled pentagons and can self-tessellate space.
Applications
Spheres centered at the vertices of the snub disphenoid form a cluster that, according to numerical experiments, has the minimum possible Lennard-Jones potential among all eight-sphere clusters.[5]
In the geometry of chemical compounds, a polyhedron may be visualized as the atom cluster surrounding a central atom. The dodecahedral molecular geometry describes the cluster for which it is a snub disphenoid.[11]
History and naming
This shape was called a Siamese dodecahedron in the paper by Hans Freudenthal and B. L. van der Waerden (1947) which first described the set of eight convex deltahedra.[12]
The dodecadeltahedron name was given to the same shape by Bernal (1964), referring to the fact that it is a 12-sided deltahedron. There are other simplicial dodecahedra, such as the hexagonal bipyramid, but this is the only one that can be realized with equilateral faces. Bernal was interested in the shapes of holes left in irregular close-packed arrangements of spheres, so he used a restrictive definition of deltahedra, in which a deltahedron is a convex polyhedron with triangular faces that can be formed by the centers of a collection of congruent spheres, whose tangencies represent polyhedron edges, and such that there is no room to pack another sphere inside the cage created by this system of spheres. This restrictive definition disallows the triangular bipyramid (as forming two tetrahedral holes rather than a single hole), pentagonal bipyramid (because the spheres for its apexes interpenetrate, so it cannot occur in sphere packings), and icosahedron (because it has interior room for another sphere). Bernal writes that the snub disphenoid is "a very common coordination for the calcium ion in crystallography".[13] In coordination geometry, it is usually known as the trigonal dodecahedron or simply as the dodecahedron.[2][citation needed]
The snub disphenoid name comes from Norman Johnson's 1966 classification of the Johnson solids, convex polyhedra all of whose faces are regular.[14] It exists first in a series of polyhedra with axial symmetry, so also can be given the name digonal gyrobianticupola.
References
- ^ Holme, Audun (2010), Geometry: Our Cultural Heritage, Springer, doi:10.1007/978-3-642-14441-7, ISBN 978-3-642-14441-7.
- ^ a b c Hartshorne, Robin (2000), Geometry: Euclid and Beyond, Undergraduate Texts in Mathematics, Springer-Verlag, p. 457, ISBN 9780387986500.
- ^ Timofeenko, A. V. (2009), "The non-Platonic and non-Archimedean noncomposite polyhedra", Journal of Mathematical Science, 162 (5): 725, doi:10.1007/s10958-009-9655-0, S2CID 120114341.
- ^ Montroll, John (2004), "Dodecadeltahedron", A Constellation of Origami Polyhedra, Dover Origami Papercraft Series, Dover Publications, Inc., pp. 38–40, ISBN 9780486439587.
- ^ a b Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H. (1995), "Minimal-energy clusters of hard spheres", Discrete and Computational Geometry, 14 (3): 237–259, doi:10.1007/BF02570704, MR 1344734.
- ^ a b Cundy, H. Martyn (1952), "Deltahedra", The Mathematical Gazette, 36 (318): 263–266, doi:10.2307/3608204, JSTOR 3608204, MR 0051525, S2CID 250435684.
- ^ Francis, Darryl (August 2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177
- ^ Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
- ^ Lawson, Kyle A.; Parish, James L.; Traub, Cynthia M.; Weyhaupt, Adam G. (2013), "Coloring graphs to classify simple closed geodesics on convex deltahedra." (PDF), International Journal of Pure and Applied Mathematics, 89 (2): 123–139, doi:10.12732/ijpam.v89i2.1, Zbl 1286.05048.
- ^ Finbow, Arthur S.; Hartnell, Bert L.; Nowakowski, Richard J.; Plummer, Michael D. (2010), "On well-covered triangulations. III", Discrete Applied Mathematics, 158 (8): 894–912, doi:10.1016/j.dam.2009.08.002, MR 2602814.
- ^ Burdett, Jeremy K.; Hoffmann, Roald; Fay, Robert C. (1978), "Eight-Coordination", Inorganic Chemistry, 17 (9): 2553–2568, doi:10.1021/ic50187a041.
- ^ Freudenthal, H.; van d. Waerden, B. L. (1947), "On an assertion of Euclid", Simon Stevin, 25: 115–121, MR 0021687.
- ^ Bernal, J. D. (1964), "The Bakerian Lecture, 1962. The Structure of Liquids", Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 280 (1382): 299–322, Bibcode:1964RSPSA.280..299B, doi:10.1098/rspa.1964.0147, JSTOR 2415872, S2CID 178710030.
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, S2CID 122006114, Zbl 0132.14603.






















