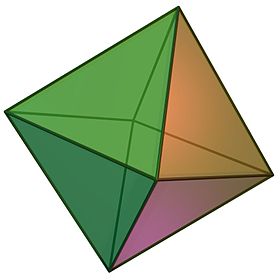
Octahedron

For the album by The Mars Volta, see Octahedron (album).

Regular Octahedron
(Click here for rotating model)
Type	Platonic solid
Elements	F = 8, E = 12 V = 6 (χ = 2)
Faces by sides	8{3}
Schläfli symbol	{3,4}
Wythoff symbol	4 | 2 3
Coxeter diagram
Symmetry	Oh, BC3, [4,3], (*432)
Rotation group	O, [4,3]+, (432)
References	U05, C17, W2
Properties	Regular convex deltahedron
Dihedral angle	109.47122° = arccos(-1/3)
3.3.3.3 (Vertex figure)	Cube (dual polyhedron)
Net

In geometry, an octahedron (plural: octahedra) is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

An octahedron is the three-dimensional case of the more general concept of a cross polytope.

Regular octahedron

Main article: Regular octahedron

Dimensions

If the edge length of a regular octahedron is a, the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is

$r_u = \frac{a}{2} \sqrt{2} \approx 0.7071067 \cdot a$

and the radius of an inscribed sphere (tangent to each of the octahedron's faces) is

$r_i = \frac{a}{6} \sqrt{6} \approx 0.4082482\cdot a$

while the midradius, which touches the middle of each edge, is

$r_m = \frac{a}{2} = 0.5\cdot a$

Orthogonal projections

The octahedron has four special orthogonal projections, centered, on an edge, vertex, face, and normal to a face. The second and third correspond to the B₂ and A₂ Coxeter planes.

Orthogonal projections

Centered by	Edge	Face Normal	Vertex	Face
Image
Projective symmetry	[2]	[2]	[4]	[6]

Cartesian coordinates

An octahedron with edge length sqrt(2) can be placed with its center at the origin and its vertices on the coordinate axes; the Cartesian coordinates of the vertices are then

( ±1, 0, 0 );

( 0, ±1, 0 );

( 0, 0, ±1 ).

In an x–y–z Cartesian coordinate system, the octahedron with center coordinates (a, b, c) and radius r is the set of all points (x, y, z) such that

$\left|x - a\right| + \left|y - b\right| + \left|z - c\right| = r.$

Area and volume

The surface area A and the volume V of a regular octahedron of edge length a are:

$A=2\sqrt{3}a^2 \approx 3.46410162a^2$

$V=\frac{1}{3} \sqrt{2}a^3 \approx 0.471404521a^3$

Thus the volume is four times that of a regular tetrahedron with the same edge length, while the surface area is twice (because we have 8 vs. 4 triangles).

If an octahedron has been stretched so that it obeys the equation:

$\left|\frac{x}{x_m}\right|+\left|\frac{y}{y_m}\right|+\left|\frac{z}{z_m}\right| = 1$

The formula for the surface area and volume expand to become:

$A=4 \, x_m \, y_m \, z_m \times \sqrt{\frac{1}{x_m^2}+\frac{1}{y_m^2}+\frac{1}{z_m^2}}$

$V=\frac{4}{3}\,x_m\,y_m\,z_m$

Additionally the inertia tensor of the stretched octahedron is:

$I = \begin{bmatrix} \frac{1}{10} m (y_m^2+z_m^2) & 0 & 0 \\ 0 & \frac{1}{10} m (x_m^2+z_m^2) & 0 \\ 0 & 0 & \frac{1}{10} m (x_m^2+y_m^2) \end{bmatrix}$

These reduce to the equations for the regular octahedron when:

$x_m=y_m=z_m=a\,\frac{\sqrt{2}}{2}$

Geometric relations

The octahedron represents the central intersection of two tetrahedra

The interior of the compound of two dual tetrahedra is an octahedron, and this compound, called the stella octangula, is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron relate to the other Platonic solids. One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of an icosahedron. This is done by first placing vectors along the octahedron's edges such that each face is bounded by a cycle, then similarly partitioning each edge into the golden mean along the direction of its vector. There are five octahedra that define any given icosahedron in this fashion, and together they define a regular compound.

Octahedra and tetrahedra can be alternated to form a vertex, edge, and face-uniform tessellation of space, called the octet truss by Buckminster Fuller. This is the only such tiling save the regular tessellation of cubes, and is one of the 28 convex uniform honeycombs. Another is a tessellation of octahedra and cuboctahedra.

The octahedron is unique among the Platonic solids in having an even number of faces meeting at each vertex. Consequently, it is the only member of that group to possess mirror planes that do not pass through any of the faces.

Using the standard nomenclature for Johnson solids, an octahedron would be called a square bipyramid. Truncation of two opposite vertices results in a square bifrustum.

The octahedron is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the pentagonal dipyramid, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.

Uniform colorings and symmetry

There are 3 uniform colorings of the octahedron, named by the triangular face colors going around each vertex: 1212, 1112, 1111.

The octahedron's symmetry group is O_h, of order 48, the three dimensional hyperoctahedral group. This group's subgroups include D_3d (order 12), the symmetry group of a triangular antiprism; D_4h (order 16), the symmetry group of a square bipyramid; and T_d (order 24), the symmetry group of a rectified tetrahedron. These symmetries can be emphasized by different colorings of the faces.

Name	Octahedron	Rectified tetrahedron (Tetratetrahedron)	Triangular antiprism	Square bipyramid	Rhombic fusil
Coxeter-Dynkin
Schläfli symbol	{3,4}	t1{3,3}	h0,1{2,6} s{2,3}	f0,1{2,4} { } + {4}	f0,1,2{2,2} { } + { } + { }
Wythoff symbol	4 | 3 2	2 | 4 3	2 | 6 2 | 2 3 2
Symmetry	Oh, [4,3], (*432)	Td, [3,3], (*332)	D3d, [2+,6], (2*3) D3, [2,3]+, (322)	D4h, [2,4], (*422)	D2h, [2,2], (*222)
Symmetry order	48	24	12 6	16	8
Image (uniform coloring)	(1111)	(1212)	(1112)

Dual

The octahedron is the dual polyhedron to the cube.

Nets

It has eleven arrangements of nets.

Irregular octahedra

The following polyhedra are combinatorially equivalent to the regular polyhedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of a regular octahedron.

• Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles.
• Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all three quadrilaterals are planar squares.
• Schönhardt polyhedron, a nonconvex polyhedron that cannot be partitioned into tetrahedra without introducing new vertices.

More generally, an octahedron can be any polyhedron with eight faces. The regular octahedron has 6 vertices and 12 edges, the minimum for an octahedron; nonregular octahedra may have as many as 12 vertices and 18 edges.[1] Other nonregular octahedra include the following:

• Hexagonal prism: Two faces are parallel regular hexagons; six squares link corresponding pairs of hexagon edges.
• Heptagonal pyramid: One face is a heptagon (usually regular), and the remaining seven faces are triangles (usually isosceles). It is not possible for all triangular faces to be equilateral.
• Truncated tetrahedron: The four faces from the tetrahedron are truncated to become regular hexagons, and there are four more equilateral triangle faces where each tetrahedron vertex was truncated.
• Tetragonal trapezohedron: The eight faces are congruent kites.

Related polyhedra

The octahedron is one of a family of uniform polyhedra related to the cube.

Uniform octahedral polyhedra

Symmetry: [4,3], (*432)							[4,3]+, (432)	[1+,4,3], (*332)	[4,3+], (3*2)
{4,3}	t0,1{4,3}	t1{4,3}	t1,2{4,3}	{3,4}	t0,2{4,3}	t0,1,2{4,3}	s{4,3}	h{4,3}	h1,2{4,3}
Duals to uniform polyhedra
V4.4.4	V3.8.8	V3.4.3.4	V4.6.6	V3.3.3.3	V3.4.4.4	V4.6.8	V3.3.3.3.4	V3.3.3	V3.3.3.3.3

The octahedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.

{3,3}

{3,4}

{3,5}

{3,6}

{3,7}

{3,8}

{3,9}

...

(3,∞}

Tetratetrahedron

The regular octahedron can also be considered a rectified tetrahedron – and can be called a tetratetrahedron. This can be shown by a 2-color face model. With this coloring, the octahedron has tetrahedral symmetry.

Compare this truncation sequence between a tetrahedron and its dual:

Family of uniform tetrahedral polyhedra

Symmetry: [3,3], (*332)							[3,3]+, (332)
{3,3}	t0,1{3,3}	t1{3,3}	t1,2{3,3}	t2{3,3}	t0,2{3,3}	t0,1,2{3,3}	s{3,3}
Duals to uniform polyhedra
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

The above shapes may also be realized as slices orthogonal to the long diagonal of a tesseract. If this diagonal is oriented vertically with a height of 1, then the first five slices above occur at heights r, 3/8, 1/2, 5/8, and s, where r is any number in the range (0,1/4], and s is any number in the range [3/4,1).

The tetratetrahedron can be seen in a sequence of quasiregular polyhedrons and tilings:

Dimensional family of quasiregular polyhedra and tilings: 3.n.3.n

Symmetry *n32 [n,3]	Spherical			Euclidean	Hyperbolic tiling
	*332 [3,3] Td	*432 [4,3] Oh	*532 [5,3] Ih	*632 [6,3] p6m	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]
Quasiregular figures configuration	3.3.3.3	3.4.3.4	3.5.3.5	3.6.3.6	3.7.3.7	3.8.3.8	3.∞.3.∞
Coxeter diagram
Dual (rhombic) figures configuration	V3.3.3.3	V3.4.3.4	V3.5.3.5	V3.6.3.6	V3.7.3.7	V3.8.3.8	V3.∞.3.∞
Coxeter diagram

Trigonal antiprism

As a trigonal antiprism, the octahedron is related to the hexagonal dihedral symmetry family.

Uniform hexagonal dihedral spherical polyhedra

Symmetry: [6,2], (*622)							[6,2]+, (622)	[1+,6,2], (322)	[6,2+], (2*3)
{6,2}	t0,1{6,2}	t1{6,2}	t1,2{6,2}	t2{6,2}	t0,2{6,2}	t0,1,2{6,2}	s{6,2}	h{6,2}	h1,2{6,2}
Uniform duals
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V32	V3.3.3.3

Family of uniform antiprisms

2	3	4	5	6	7	8	9	10	11	12	...
As spherical polyhedra

Square bipyramid

Family of bipyramids

2	3	4	5	6	7	8	9	10	11	12	...	∞
As spherical polyhedra

Tetrahemihexahedron

The regular octahedron shares its edges and vertex arrangement with one nonconvex uniform polyhedron: the tetrahemihexahedron, with which it shares four of the triangular faces.

Octahedron

Tetrahemihexahedron

Tetrahedral Truss

A framework of repeating tetrahedrons and octahedrons was invented by Buckminster Fuller in the 1950s, known as a space frame, commonly regarded as the strongest structure for resisting cantilever stresses.

Octahedra in the physical world

Octahedra in nature

Fluorite octahedron.

• Natural crystals of diamond, alum or fluorite are commonly octahedral, as the space-filling tetrahedral-octahedral honeycomb.
• The plates of kamacite alloy in octahedrite meteorites are arranged paralleling the eight faces of an octahedron.
• Many metal ions coordinate six ligands in an octahedral or distorted octahedral configuration.
• Widmanstätten patterns in nickel-iron crystals

Octahedra in art and culture

Two identically formed rubik's snakes can approximate an octahedron.

• Especially in roleplaying games, this solid is known as a "d8", one of the more common non-cubical dice.
• If each edge of an octahedron is replaced by a one ohm resistor, the resistance between opposite vertices is 1/2 ohms, and that between adjacent vertices 5/12 ohms.
• Six musical notes can be arranged on the vertices of an octahedron in such a way that each edge represents a consonant dyad and each face represents a consonant triad; see hexany.

See also

• Spinning octahedron
• Stella octangula
• Triakis octahedron
• Hexakis octahedron
• Truncated octahedron
• Octahedral molecular geometry
• Octahedral symmetry
• Octahedral graph

External links

• Weisstein, Eric W., "Octahedron", MathWorld.
• Richard Klitzing, 3D convex uniform polyhedra, x3o4o - oct
• Editable printable net of an octahedron with interactive 3D view
• Paper model of the octahedron
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra