Flux tube
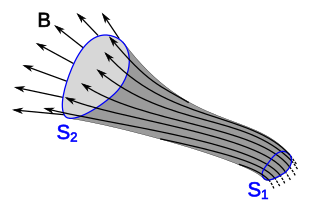
A flux tube is a generally tube-like (cylindrical) region of space containing a magnetic field, B, such that the cylindrical sides of the tube are everywhere parallel to the magnetic field lines. It is a graphical visual aid for visualizing a magnetic field. Since no magnetic flux passes through the sides of the tube, the flux through any cross section of the tube is equal, and the flux entering the tube at one end is equal to the flux leaving the tube at the other. Both the cross-sectional area of the tube and the magnetic field strength may vary along the length of the tube, but the magnetic flux inside is always constant.
As used in astrophysics, a flux tube generally means an area of space through which a strong magnetic field passes, in which the behavior of matter (usually ionized gas or plasma) is strongly influenced by the field. They are commonly found around stars, including the Sun, which has many flux tubes from tens to hundreds of kilometers in diameter.[1] Sunspots are also associated with larger flux tubes of 2500 km diameter.[1] Some planets also have flux tubes. A well-known example is the flux tube between Jupiter and its moon Io.
Definition
[edit]This article or section appears to contradict itself. (January 2023) |
The flux of a vector field passing through any closed orientable surface is the surface integral of the field over the surface. For example, for a vector field consisting of the velocity of a volume of liquid in motion, and an imaginary surface within the liquid, the flux is the volume of liquid passing through the surface per unit time.
A flux tube can be defined passing through any closed, orientable surface in a vector field , as the set of all points on the field lines passing through the boundary of . This set forms a hollow tube. The tube follows the field lines, possibly turning, twisting, and changing its cross sectional size and shape as the field lines converge or diverge. Since no field lines pass through the tube walls there is no flux through the walls of the tube, so all the field lines enter and leave through the end surfaces. Thus a flux tube divides all the field lines into two sets; those passing through the inside of the tube, and those outside. Consider the volume bounded by the tube and any two surfaces and intersecting it. If the field has sources or sinks within the tube the flux out of this volume will be nonzero. However, if the field is divergenceless (solenoidal, ) then from the divergence theorem the sum of the flux leaving the volume through these two surfaces will be zero, so the flux leaving through will be equal to the flux entering through . In other words, the flux within the tube through any surface intersecting the tube is equal, the tube encloses a constant quantity of flux along its length. The strength (magnitude) of the vector field, and the cross sectional area of the tube varies along its length, but the surface integral of the field over any surface spanning the tube is equal.
Since from Maxwell's equations (specifically Gauss's law for magnetism) magnetic fields are divergenceless, magnetic flux tubes have this property, so flux tubes are mainly used as an aid in visualizing magnetic fields. However flux tubes can also be useful for visualizing other vector fields in regions of zero divergence, such as electric fields in regions where there are no charges and gravitational fields in regions where there is no mass.
In particle physics, the hadron particles that make up all matter, such as neutrons and protons, are composed of more basic particles called quarks, which are bound together by thin flux tubes of strong nuclear force field. The flux tube model is important in explaining the so-called color confinement mechanism, why quarks are never seen separately in particle experiments.
Types
[edit]- Flux rope: Twisted magnetic flux tube.[1]
- Fibril field: Magnetic flux tube that does not have a magnetic field outside the tube.[1]
History
[edit]In 1861, James Clerk Maxwell gave rise to the concept of a flux tube inspired by Michael Faraday's work in electrical and magnetic behavior in his paper titled "On Physical Lines of Force".[2] Maxwell described flux tubes as:
If upon any surface which cuts the lines of fluid motion we draw a closed curve, and if from every point of this curve we draw lines of motion, these lines of motion will generate a tubular surface which we may call a tube of fluid motion.[3]
Flux tube strength
[edit]The flux tube's strength, , is defined to be the magnetic flux through a surface intersecting the tube, equal to the surface integral of the magnetic field over Since the magnetic field is solenoidal, as defined in Maxwell's equations (specifically Gauss' law for magnetism): .[4] the strength is constant at any surface along a flux tube. Under the condition that the cross-sectional area, , of the flux tube is small enough that the magnetic field is approximately constant, can be approximated as .[4] Therefore, if the cross sectional area of the tube decreases along the tube from to , then the magnetic field strength must increase proportionally from to in order to satisfy the condition of constant flux F.[5]
Plasma physics
[edit]Flux conservation
[edit]In magnetohydrodynamics, Alfvén's theorem states that the magnetic flux through a surface, such as the surface of a flux tube, moving along with a perfectly conducting fluid is conserved. In other words, the magnetic field is constrained to move with the fluid or is "frozen-in" to the fluid.
This can be shown mathematically for a flux tube using the induction equation of a perfectly conducting fluid where is the magnetic field and is the velocity field of the fluid. The change in magnetic flux over time through any open surface of the flux tube enclosed by with a differential line element can be written as . Using the induction equation gives which can be rewritten using Stokes' theorem and an elementary vector identity on the first and second term, respectively, to give[6]
Compression and extension
[edit]In ideal magnetohydrodynamics, if a cylindrical flux tube of length is compressed while the length of tube stays the same, the magnetic field and the density of the tube increase with the same proportionality. If a flux tube with a configuration of a magnetic field of and a plasma density of confined to the tube is compressed by a scalar value defined as , the new magnetic field and density are given by:[4] If , known as transverse compression, and increase and are scaled the same while transverse expansion decreases and by the same value and proportion where is constant.[4]
Extending the length of the flux tube by gives a new length of while the density of the tube remains the same, , which then results in the magnetic field strength increasing by . Reducing the length of the tubes results in a decrease of the magnetic field's strength.[4]
Plasma pressure
[edit]In magnetohydrostatic equilibrium, the following condition is met for the equation of motion of the plasma confined to the flux tube:[4] where
- is the plasma pressure
- is the current density of the plasma
- is the gravitational force
With the magnetohydrostatic equilibrium condition met, a cylindrical flux tube's plasma pressure of is given by the following relation written in cylindrical coordinates with as the distance from the axis radially:[4] The second term in the above equation gives the magnetic pressure force while the third term represents the magnetic tension force.[4] The field line's twist around the axis from one end of the tube of length to the other end is given by:[4]
Examples
[edit]Solar
[edit]
Examples of solar flux tubes include sunspots and intense magnetic tubes in the photosphere and the field around the solar prominence and coronal loops in the corona.[4]
Sunspots occur when small flux tubes combine into a large flux tube that breaks the surface of the photosphere.[1] The large flux tube of the sunspot has a field intensity of around 3 kG with a diameter of typically 4000 km.[1] There are extreme cases of when the large flux tubes have diameters of km with a field strength of 3 kG.[1] Sunspots can continue to grow as long as there is a constant supply of new flux from small flux tubes on the surface of the Sun.[1] The magnetic field within the flux tube can be compressed by decreasing the gas pressure inside and therefore the internal temperature of the tube while maintaining a constant pressure outside.[1]
Intense magnetic tubes are isolated flux tubes that have diameters of 100 to 300 km with an overall field strength of 1 to 2 kG and a flux of around Wb.[4] These flux tubes are concentrated strong magnetic fields that are found between solar granules.[7] The magnetic field causes the plasma pressure in the flux tube to decrease, known as the plasma density depletion region.[7] If there is a significant difference in the temperatures in the flux tube and the surroundings, there is a decrease in plasma pressure as well as a decrease in the plasma density causing some of the magnetic field to escape the plasma.[7]
Plasma that is trapped within magnetic flux tubes that are attached to the photosphere, referred to as footpoints, create a loop-like structure known as a coronal loop.[8] The plasma inside the loop has a higher temperature than the surroundings causing the pressure and density of the plasma to increase.[8] These coronal loops get their characteristic high luminosity and ranges of shapes from the behavior of the magnetic flux tube.[8] These flux tubes confine plasma and are characterized as isolated. The confined magnetic field strength varies from 0.1 to 10 G with diameters ranging from 200 to 300 km.[8][9]
The result of emerging twisted flux tubes from the interior of the Sun cause twisted magnetic structures in the corona, which then lead to solar prominences.[10] Solar prominences are modeled using twisted magnetic flux tubes known as flux ropes.[11]
Planetary
[edit]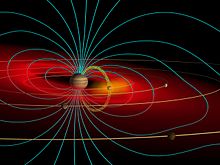
Magnetized planets have an area above their ionospheres which traps energetic particles and plasma along magnetic fields, referred to as magnetospheres.[12] The extension of the magnetosphere away from the sun known as a magnetotail is modeled as magnetic flux tubes.[12] Mars and Venus both have strong magnetic fields resulting in flux tubes from the solar wind gathering at high altitudes of the ionosphere on the sun side of the planets and causing the flux tubes to distort along the magnetic field lines creating flux ropes.[12] Particles from the solar wind magnetic field lines can transfer to the magnetic field lines of a planet's magnetosphere through the processes of magnetic reconnection that occurs when a flux tube from the solar wind and a flux tube from the magnetosphere in opposite field directions get close to one another.[12]
Flux tubes that occur from magnetic reconnection forms into a dipole-like configuration around the planet where plasma flow occurs.[12] An example of this case is the flux tube between Jupiter and its moon Io approximately 450 km in diameter at the points closest to Jupiter.[13]
See also
[edit]- QCD string, sometimes called a flux tube
- Flux transfer event
- Birkeland current
- Magnetohydrodynamics (MHD)
- Marklund convection
References
[edit]- ^ a b c d e f g h i Parker, E. N. (1979). "Sunspots and the Physics of Magnetic Flux Tubes. I The General Nature of the Sunspot". The Astrophysical Journal. 230: 905–913. Bibcode:1979ApJ...230..905P. doi:10.1086/157150.
- ^ Roberts, B (1990). "Waves in Magnetic Flux Tubes". Basic Plasma Processes on the Sun: Proceedings of the 142nd Symposium of the International Astronomical Union Held in Bangalore, India, December 1–5, 1989. Edition 1.
- ^ Maxwell, J. C. (1861). "On Physical Lines of Force". Philosophical Magazine and Journal of Science. 4.
- ^ a b c d e f g h i j k Priest, E. (2014). Magnetohydrodynamics of the Sun. Cambridge University Press. pp. 100–103. ISBN 978-0-521-85471-9.
- ^ Priest, E. R.; Forbes, T. G. (2001). "Magnetohydrodynamics" (PDF). Nature. Archived from the original (PDF) on 2017-11-09. Retrieved 2017-04-18.
- ^ Parker, E. N. (1979). Cosmic Magnetic Fields Their Origin and Their Activity. Bristol, UK: Oxford University Press. ISBN 0-19-851290-2.
- ^ a b c Roberts, B. (2001). "Solar Photospheric Magnetic Flux Tubes: Theory" (PDF). Encyclopedia of Astronomy and Astrophysics. doi:10.1888/0333750888/2255. ISBN 0333750888.
- ^ a b c d Reale, F. (2014). "Coronal Loops: Observations and Modeling of Confined Plasma". Living Reviews in Solar Physics. 11 (1): 4. arXiv:1010.5927. Bibcode:2014LRSP...11....4R. doi:10.12942/lrsp-2014-4. PMC 4841190. PMID 27194957.
- ^ Peter, H.; et al. (2013). "Structure of Solar Coronal Loops: from Miniature to Large-Scale". Astronomy & Astrophysics. 556: A104. arXiv:1306.4685. Bibcode:2013A&A...556A.104P. doi:10.1051/0004-6361/201321826. S2CID 119237311.
- ^ Fan, Y. (2015). Solar Prominences. Springer. ISBN 978-3-319-10416-4.
- ^ Jibben, P.R.; et al. (2016). "Evidence for a Magnetic Flux Rope in Observations of a Solar Prominence-Cavity System". Frontiers in Astronomy and Space Sciences. 3: 10. Bibcode:2016FrASS...3...10J. doi:10.3389/fspas.2016.00010.
- ^ a b c d e Kivelson, M. G.; Bagenal, F. (2007). "Planetary Magnetospheres" (PDF). pp. 519–540. Bibcode:2007ess..book..519K. doi:10.1016/B978-012088589-3/50032-3. ISBN 9780120885893.
{{cite book}}:|journal=ignored (help); Missing or empty|title=(help) - ^ Bhardwaj, A.; Gladstone, G. R.; Zarka, P. (2001). "An Overview of Io Flux Tube Footpoints in Juptier's Auroral Ionosphere". Advances in Space Research. 27 (11): 1915–1922. Bibcode:2001AdSpR..27.1915B. doi:10.1016/s0273-1177(01)00280-0.
















































