Random forest
| Part of a series on |
| Machine learning and data mining |
|---|
Random forests or random decision forests is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time. For classification tasks, the output of the random forest is the class selected by most trees. For regression tasks, the mean or average prediction of the individual trees is returned.[1][2] Random decision forests correct for decision trees' habit of overfitting to their training set.[3]: 587–588
The first algorithm for random decision forests was created in 1995 by Tin Kam Ho[1] using the random subspace method,[2] which, in Ho's formulation, is a way to implement the "stochastic discrimination" approach to classification proposed by Eugene Kleinberg.[4][5][6]
An extension of the algorithm was developed by Leo Breiman[7] and Adele Cutler,[8] who registered[9] "Random Forests" as a trademark in 2006 (as of 2019[update], owned by Minitab, Inc.).[10] The extension combines Breiman's "bagging" idea and random selection of features, introduced first by Ho[1] and later independently by Amit and Geman[11] in order to construct a collection of decision trees with controlled variance.
History
[edit]The general method of random decision forests was first proposed by Salzberg and Heath in 1993,[12] with a method that used a randomized decision tree algorithm to generate multiple different trees and then combine them using majority voting. This idea was developed further by Ho in 1995.[1] Ho established that forests of trees splitting with oblique hyperplanes can gain accuracy as they grow without suffering from overtraining, as long as the forests are randomly restricted to be sensitive to only selected feature dimensions. A subsequent work along the same lines[2] concluded that other splitting methods behave similarly, as long as they are randomly forced to be insensitive to some feature dimensions. Note that this observation of a more complex classifier (a larger forest) getting more accurate nearly monotonically is in sharp contrast to the common belief that the complexity of a classifier can only grow to a certain level of accuracy before being hurt by overfitting. The explanation of the forest method's resistance to overtraining can be found in Kleinberg's theory of stochastic discrimination.[4][5][6]
The early development of Breiman's notion of random forests was influenced by the work of Amit and Geman[11] who introduced the idea of searching over a random subset of the available decisions when splitting a node, in the context of growing a single tree. The idea of random subspace selection from Ho[2] was also influential in the design of random forests. In this method a forest of trees is grown, and variation among the trees is introduced by projecting the training data into a randomly chosen subspace before fitting each tree or each node. Finally, the idea of randomized node optimization, where the decision at each node is selected by a randomized procedure, rather than a deterministic optimization was first introduced by Thomas G. Dietterich.[13]
The proper introduction of random forests was made in a paper by Leo Breiman.[7] This paper describes a method of building a forest of uncorrelated trees using a CART like procedure, combined with randomized node optimization and bagging. In addition, this paper combines several ingredients, some previously known and some novel, which form the basis of the modern practice of random forests, in particular:
- Using out-of-bag error as an estimate of the generalization error.
- Measuring variable importance through permutation.
The report also offers the first theoretical result for random forests in the form of a bound on the generalization error which depends on the strength of the trees in the forest and their correlation.
Algorithm
[edit]Preliminaries: decision tree learning
[edit]Decision trees are a popular method for various machine learning tasks. Tree learning "come[s] closest to meeting the requirements for serving as an off-the-shelf procedure for data mining", say Hastie et al., "because it is invariant under scaling and various other transformations of feature values, is robust to inclusion of irrelevant features, and produces inspectable models. However, they are seldom accurate".[3]: 352
In particular, trees that are grown very deep tend to learn highly irregular patterns: they overfit their training sets, i.e. have low bias, but very high variance. Random forests are a way of averaging multiple deep decision trees, trained on different parts of the same training set, with the goal of reducing the variance.[3]: 587–588 This comes at the expense of a small increase in the bias and some loss of interpretability, but generally greatly boosts the performance in the final model.
Bagging
[edit]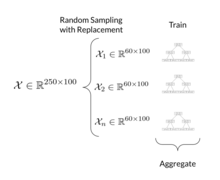
The training algorithm for random forests applies the general technique of bootstrap aggregating, or bagging, to tree learners. Given a training set X = x1, ..., xn with responses Y = y1, ..., yn, bagging repeatedly (B times) selects a random sample with replacement of the training set and fits trees to these samples:
- Sample, with replacement, n training examples from X, Y; call these Xb, Yb.
- Train a classification or regression tree fb on Xb, Yb.
After training, predictions for unseen samples x' can be made by averaging the predictions from all the individual regression trees on x':
or by taking the plurality vote in the case of classification trees.
This bootstrapping procedure leads to better model performance because it decreases the variance of the model, without increasing the bias. This means that while the predictions of a single tree are highly sensitive to noise in its training set, the average of many trees is not, as long as the trees are not correlated. Simply training many trees on a single training set would give strongly correlated trees (or even the same tree many times, if the training algorithm is deterministic); bootstrap sampling is a way of de-correlating the trees by showing them different training sets.
Additionally, an estimate of the uncertainty of the prediction can be made as the standard deviation of the predictions from all the individual regression trees on x′:
The number of samples/trees, B, is a free parameter. Typically, a few hundred to several thousand trees are used, depending on the size and nature of the training set. An optimal number of trees B can be found using cross-validation, or by observing the out-of-bag error: the mean prediction error on each training sample xi, using only the trees that did not have xi in their bootstrap sample.[14] The training and test error tend to level off after some number of trees have been fit.
From bagging to random forests
[edit]The above procedure describes the original bagging algorithm for trees. Random forests also include another type of bagging scheme: they use a modified tree learning algorithm that selects, at each candidate split in the learning process, a random subset of the features. This process is sometimes called "feature bagging". The reason for doing this is the correlation of the trees in an ordinary bootstrap sample: if one or a few features are very strong predictors for the response variable (target output), these features will be selected in many of the B trees, causing them to become correlated. An analysis of how bagging and random subspace projection contribute to accuracy gains under different conditions is given by Ho.[15]
Typically, for a classification problem with p features, √p (rounded down) features are used in each split.[3]: 592 For regression problems the inventors recommend p/3 (rounded down) with a minimum node size of 5 as the default.[3]: 592 In practice, the best values for these parameters should be tuned on a case-to-case basis for every problem.[3]: 592
ExtraTrees
[edit]Adding one further step of randomization yields extremely randomized trees, or ExtraTrees. While similar to ordinary random forests in that they are an ensemble of individual trees, there are two main differences: first, each tree is trained using the whole learning sample (rather than a bootstrap sample), and second, the top-down splitting in the tree learner is randomized. Instead of computing the locally optimal cut-point for each feature under consideration (based on, e.g., information gain or the Gini impurity), a random cut-point is selected. This value is selected from a uniform distribution within the feature's empirical range (in the tree's training set). Then, of all the randomly generated splits, the split that yields the highest score is chosen to split the node. Similar to ordinary random forests, the number of randomly selected features to be considered at each node can be specified. Default values for this parameter are for classification and for regression, where is the number of features in the model.[16]
Random forests for high-dimensional data
[edit]The basic Random Forest procedure may not work well in situations where there are a large number of features but only a small proportion of these features are informative with respect to sample classification. This can be addressed by encouraging the procedure to focus mainly on features and trees that are informative. Some methods for accomplishing this are:
- Prefiltering: Eliminate features that are mostly just noise.[17][18]
- Enriched Random Forest (ERF): Use weighted random sampling instead of simple random sampling at each node of each tree, giving greater weight to features that appear to be more informative.[19][20]
- Tree Weighted Random Forest (TWRF): Weight trees so that trees exhibiting better accuracy are assigned higher weights.[21][22]
Properties
[edit]Variable importance
[edit]Random forests can be used to rank the importance of variables in a regression or classification problem in a natural way. The following technique was described in Breiman's original paper[7] and is implemented in the R package randomForest.[8]
Permutation Importance
[edit]The first step in measuring the variable importance in a data set is to fit a random forest to the data. During the fitting process the out-of-bag error for each data point is recorded and averaged over the forest (errors on an independent test set can be substituted if bagging is not used during training).
To measure the importance of the -th feature after training, the values of the -th feature are permuted in the out-of-bag samples and the out-of-bag error is again computed on this perturbed data set. The importance score for the -th feature is computed by averaging the difference in out-of-bag error before and after the permutation over all trees. The score is normalized by the standard deviation of these differences.
Features which produce large values for this score are ranked as more important than features which produce small values. The statistical definition of the variable importance measure was given and analyzed by Zhu et al.[23]
This method of determining variable importance has some drawbacks.
- For data including categorical variables with different number of levels, random forests are biased in favor of those attributes with more levels. Methods such as partial permutations[24][25][26] and growing unbiased trees[27][28] can be used to solve the problem.
- If the data contain groups of correlated features of similar relevance for the output, then smaller groups are favored over larger groups.[29]
- Additionally, the permutation procedure may fail to identify important features when there are collinear features. In this case permuting groups of correlated features together is a remedy.[30]
Mean Decrease in Impurity Feature Importance
[edit]This feature importance for random forests is the default implementation in sci-kit learn and R. It is described in the book "Classification and Regression Trees" by Leo Breiman.[31] Variables which decrease the impurity during splits a lot are considered important:[32] where indicates a feature, is the number of trees in the forest, indicates tree , is the fraction of samples reaching node , is the change in impurity in tree at node . As impurity measure for samples falling in a node e.g. the following statistics can be used:
The normalized importance is then obtained by normalizing over all features, so that the sum of normalized feature importances is 1.
The sci-kit learn default implementation of Mean Decrease in Impurity Feature Importance is susceptible to misleading feature importances:[30]
- the importance measure prefers high cardinality features
- it uses training statistics and therefore does not "reflect the ability of feature to be useful to make predictions that generalize to the test set"[33]
Relationship to nearest neighbors
[edit]A relationship between random forests and the k-nearest neighbor algorithm (k-NN) was pointed out by Lin and Jeon in 2002.[34] It turns out that both can be viewed as so-called weighted neighborhoods schemes. These are models built from a training set that make predictions for new points x' by looking at the "neighborhood" of the point, formalized by a weight function W:
Here, is the non-negative weight of the i'th training point relative to the new point x' in the same tree. For any particular x', the weights for points must sum to one. Weight functions are given as follows:
- In k-NN, the weights are if xi is one of the k points closest to x', and zero otherwise.
- In a tree, if xi is one of the k' points in the same leaf as x', and zero otherwise.
Since a forest averages the predictions of a set of m trees with individual weight functions , its predictions are
This shows that the whole forest is again a weighted neighborhood scheme, with weights that average those of the individual trees. The neighbors of x' in this interpretation are the points sharing the same leaf in any tree . In this way, the neighborhood of x' depends in a complex way on the structure of the trees, and thus on the structure of the training set. Lin and Jeon show that the shape of the neighborhood used by a random forest adapts to the local importance of each feature.[34]
Unsupervised learning with random forests
[edit]As part of their construction, random forest predictors naturally lead to a dissimilarity measure among the observations. One can also define a random forest dissimilarity measure between unlabeled data: the idea is to construct a random forest predictor that distinguishes the "observed" data from suitably generated synthetic data.[7][35] The observed data are the original unlabeled data and the synthetic data are drawn from a reference distribution. A random forest dissimilarity can be attractive because it handles mixed variable types very well, is invariant to monotonic transformations of the input variables, and is robust to outlying observations. The random forest dissimilarity easily deals with a large number of semi-continuous variables due to its intrinsic variable selection; for example, the "Addcl 1" random forest dissimilarity weighs the contribution of each variable according to how dependent it is on other variables. The random forest dissimilarity has been used in a variety of applications, e.g. to find clusters of patients based on tissue marker data.[36]
Variants
[edit]Instead of decision trees, linear models have been proposed and evaluated as base estimators in random forests, in particular multinomial logistic regression and naive Bayes classifiers.[37][38][39] In cases that the relationship between the predictors and the target variable is linear, the base learners may have an equally high accuracy as the ensemble learner.[40][37]
Kernel random forest
[edit]In machine learning, kernel random forests (KeRF) establish the connection between random forests and kernel methods. By slightly modifying their definition, random forests can be rewritten as kernel methods, which are more interpretable and easier to analyze.[41]
History
[edit]Leo Breiman[42] was the first person to notice the link between random forest and kernel methods. He pointed out that random forests which are grown using i.i.d. random vectors in the tree construction are equivalent to a kernel acting on the true margin. Lin and Jeon[43] established the connection between random forests and adaptive nearest neighbor, implying that random forests can be seen as adaptive kernel estimates. Davies and Ghahramani[44] proposed Random Forest Kernel and show that it can empirically outperform state-of-art kernel methods. Scornet[41] first defined KeRF estimates and gave the explicit link between KeRF estimates and random forest. He also gave explicit expressions for kernels based on centered random forest[45] and uniform random forest,[46] two simplified models of random forest. He named these two KeRFs Centered KeRF and Uniform KeRF, and proved upper bounds on their rates of consistency.
Notations and definitions
[edit]Preliminaries: Centered forests
[edit]Centered forest[45] is a simplified model for Breiman's original random forest, which uniformly selects an attribute among all attributes and performs splits at the center of the cell along the pre-chosen attribute. The algorithm stops when a fully binary tree of level is built, where is a parameter of the algorithm.
Uniform forest
[edit]Uniform forest[46] is another simplified model for Breiman's original random forest, which uniformly selects a feature among all features and performs splits at a point uniformly drawn on the side of the cell, along the preselected feature.
From random forest to KeRF
[edit]Given a training sample of -valued independent random variables distributed as the independent prototype pair , where . We aim at predicting the response , associated with the random variable , by estimating the regression function . A random regression forest is an ensemble of randomized regression trees. Denote the predicted value at point by the -th tree, where are independent random variables, distributed as a generic random variable , independent of the sample . This random variable can be used to describe the randomness induced by node splitting and the sampling procedure for tree construction. The trees are combined to form the finite forest estimate . For regression trees, we have , where is the cell containing , designed with randomness and dataset , and .
Thus random forest estimates satisfy, for all , . Random regression forest has two levels of averaging, first over the samples in the target cell of a tree, then over all trees. Thus the contributions of observations that are in cells with a high density of data points are smaller than that of observations which belong to less populated cells. In order to improve the random forest methods and compensate the misestimation, Scornet[41] defined KeRF by which is equal to the mean of the 's falling in the cells containing in the forest. If we define the connection function of the finite forest as , i.e. the proportion of cells shared between and , then almost surely we have , which defines the KeRF.
Centered KeRF
[edit]The construction of Centered KeRF of level is the same as for centered forest, except that predictions are made by , the corresponding kernel function, or connection function is
Uniform KeRF
[edit]Uniform KeRF is built in the same way as uniform forest, except that predictions are made by , the corresponding kernel function, or connection function is
Properties
[edit]Relation between KeRF and random forest
[edit]Predictions given by KeRF and random forests are close if the number of points in each cell is controlled:
Assume that there exist sequences such that, almost surely, Then almost surely,
Relation between infinite KeRF and infinite random forest
[edit]When the number of trees goes to infinity, then we have infinite random forest and infinite KeRF. Their estimates are close if the number of observations in each cell is bounded:
Assume that there exist sequences such that, almost surely
Then almost surely,
Consistency results
[edit]Assume that , where is a centered Gaussian noise, independent of , with finite variance . Moreover, is uniformly distributed on and is Lipschitz. Scornet[41] proved upper bounds on the rates of consistency for centered KeRF and uniform KeRF.
Consistency of centered KeRF
[edit]Providing and , there exists a constant such that, for all , .
Consistency of uniform KeRF
[edit]Providing and , there exists a constant such that, .
Disadvantages
[edit]While random forests often achieve higher accuracy than a single decision tree, they sacrifice the intrinsic interpretability present in decision trees. Decision trees are among a fairly small family of machine learning models that are easily interpretable along with linear models, rule-based models, and attention-based models. This interpretability is one of the most desirable qualities of decision trees. It allows developers to confirm that the model has learned realistic information from the data and allows end-users to have trust and confidence in the decisions made by the model.[37][3] For example, following the path that a decision tree takes to make its decision is quite trivial, but following the paths of tens or hundreds of trees is much harder. To achieve both performance and interpretability, some model compression techniques allow transforming a random forest into a minimal "born-again" decision tree that faithfully reproduces the same decision function.[37][47][48] If it is established that the predictive attributes are linearly correlated with the target variable, using random forest may not enhance the accuracy of the base learner.[37][40] Furthermore, in problems with multiple categorical variables, random forest may not be able to increase the accuracy of the base learner.[49]
See also
[edit]- Boosting – Method in machine learning
- Decision tree learning – Machine learning algorithm
- Ensemble learning – Statistics and machine learning technique
- Gradient boosting – Machine learning technique
- Non-parametric statistics – Type of statistical analysis
- Randomized algorithm – Algorithm that employs a degree of randomness as part of its logic or procedure
References
[edit]- ^ a b c d Ho, Tin Kam (1995). Random Decision Forests (PDF). Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, 14–16 August 1995. pp. 278–282. Archived from the original (PDF) on 17 April 2016. Retrieved 5 June 2016.
- ^ a b c d Ho TK (1998). "The Random Subspace Method for Constructing Decision Forests" (PDF). IEEE Transactions on Pattern Analysis and Machine Intelligence. 20 (8): 832–844. doi:10.1109/34.709601. S2CID 206420153.
- ^ a b c d e f g Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning (2nd ed.). Springer. ISBN 0-387-95284-5.
- ^ a b Kleinberg E (1990). "Stochastic Discrimination" (PDF). Annals of Mathematics and Artificial Intelligence. 1 (1–4): 207–239. CiteSeerX 10.1.1.25.6750. doi:10.1007/BF01531079. S2CID 206795835. Archived from the original (PDF) on 2018-01-18.
- ^ a b Kleinberg E (1996). "An Overtraining-Resistant Stochastic Modeling Method for Pattern Recognition". Annals of Statistics. 24 (6): 2319–2349. doi:10.1214/aos/1032181157. MR 1425956.
- ^ a b Kleinberg E (2000). "On the Algorithmic Implementation of Stochastic Discrimination" (PDF). IEEE Transactions on Pattern Analysis and Machine Intelligence. 22 (5): 473–490. CiteSeerX 10.1.1.33.4131. doi:10.1109/34.857004. S2CID 3563126. Archived from the original (PDF) on 2018-01-18.
- ^ a b c d Breiman L (2001). "Random Forests". Machine Learning. 45 (1): 5–32. Bibcode:2001MachL..45....5B. doi:10.1023/A:1010933404324.
- ^ a b Liaw A (16 October 2012). "Documentation for R package randomForest" (PDF). Retrieved 15 March 2013.
- ^ U.S. trademark registration number 3185828, registered 2006/12/19.
- ^ "RANDOM FORESTS Trademark of Health Care Productivity, Inc. - Registration Number 3185828 - Serial Number 78642027 :: Justia Trademarks".
- ^ a b Amit Y, Geman D (1997). "Shape quantization and recognition with randomized trees" (PDF). Neural Computation. 9 (7): 1545–1588. CiteSeerX 10.1.1.57.6069. doi:10.1162/neco.1997.9.7.1545. S2CID 12470146. Archived from the original (PDF) on 2018-02-05. Retrieved 2008-04-01.
- ^ Heath, D., Kasif, S. and Salzberg, S. (1993). k-DT: A multi-tree learning method. In Proceedings of the Second Intl. Workshop on Multistrategy Learning, pp. 138-149.
- ^ Dietterich, Thomas (2000). "An Experimental Comparison of Three Methods for Constructing Ensembles of Decision Trees: Bagging, Boosting, and Randomization". Machine Learning. 40 (2): 139–157. doi:10.1023/A:1007607513941.
- ^ Gareth James; Daniela Witten; Trevor Hastie; Robert Tibshirani (2013). An Introduction to Statistical Learning. Springer. pp. 316–321.
- ^ Ho, Tin Kam (2002). "A Data Complexity Analysis of Comparative Advantages of Decision Forest Constructors" (PDF). Pattern Analysis and Applications. 5 (2): 102–112. doi:10.1007/s100440200009. S2CID 7415435. Archived from the original (PDF) on 2016-04-17. Retrieved 2015-11-13.
- ^ Geurts P, Ernst D, Wehenkel L (2006). "Extremely randomized trees" (PDF). Machine Learning. 63: 3–42. doi:10.1007/s10994-006-6226-1.
- ^ Dessi, N. & Milia, G. & Pes, B. (2013). Enhancing random forests performance in microarray data classification. Conference paper, 99-103. 10.1007/978-3-642-38326-7_15.
- ^ Ye, Y., Li, H., Deng, X., and Huang, J. (2008) Feature weighting random forest for detection of hidden web search interfaces. Journal of Computational Linguistics and Chinese Language Processing, 13, 387–404.
- ^ Amaratunga, D., Cabrera, J., Lee, Y.S. (2008) Enriched Random Forest. Bioinformatics, 24, 2010-2014.
- ^ Ghosh D, Cabrera J. (2022) Enriched random forest for high dimensional genomic data. IEEE/ACM Trans Comput Biol Bioinform. 19(5):2817-2828. doi:10.1109/TCBB.2021.3089417.
- ^ Winham, Stacey & Freimuth, Robert & Biernacka, Joanna. (2013). A weighted random forests approach to improve predictive performance. Statistical Analysis and Data Mining. 6. 10.1002/sam.11196.
- ^ Li, H. B., Wang, W., Ding, H. W., & Dong, J. (2010, 10-12 Nov. 2010). Trees weighting random forest method for classifying high-dimensional noisy data. Paper presented at the 2010 IEEE 7th International Conference on E-Business Engineering.
- ^ Zhu R, Zeng D, Kosorok MR (2015). "Reinforcement Learning Trees". Journal of the American Statistical Association. 110 (512): 1770–1784. doi:10.1080/01621459.2015.1036994. PMC 4760114. PMID 26903687.
- ^ Deng, H.; Runger, G.; Tuv, E. (2011). Bias of importance measures for multi-valued attributes and solutions. Proceedings of the 21st International Conference on Artificial Neural Networks (ICANN). pp. 293–300.
- ^ Altmann A, Toloşi L, Sander O, Lengauer T (May 2010). "Permutation importance: a corrected feature importance measure". Bioinformatics. 26 (10): 1340–7. doi:10.1093/bioinformatics/btq134. PMID 20385727.
- ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-06-01). "Role of Data Analytics in Infrastructure Asset Management: Overcoming Data Size and Quality Problems". Journal of Transportation Engineering, Part B: Pavements. 146 (2): 04020022. doi:10.1061/JPEODX.0000175. S2CID 216485629.
- ^ Strobl C, Boulesteix AL, Augustin T (2007). "Unbiased split selection for classification trees based on the Gini index" (PDF). Computational Statistics & Data Analysis. 52: 483–501. CiteSeerX 10.1.1.525.3178. doi:10.1016/j.csda.2006.12.030.
- ^ Painsky A, Rosset S (2017). "Cross-Validated Variable Selection in Tree-Based Methods Improves Predictive Performance". IEEE Transactions on Pattern Analysis and Machine Intelligence. 39 (11): 2142–2153. arXiv:1512.03444. doi:10.1109/tpami.2016.2636831. PMID 28114007. S2CID 5381516.
- ^ Tolosi L, Lengauer T (July 2011). "Classification with correlated features: unreliability of feature ranking and solutions". Bioinformatics. 27 (14): 1986–94. doi:10.1093/bioinformatics/btr300. PMID 21576180.
- ^ a b "Beware Default Random Forest Importances". explained.ai. Retrieved 2023-10-25.
- ^ Breiman, Leo (2017-10-25). Classification and Regression Trees. New York: Routledge. doi:10.1201/9781315139470. ISBN 978-1-315-13947-0.
- ^ Ortiz-Posadas, Martha Refugio (2020-02-29). Pattern Recognition Techniques Applied to Biomedical Problems. Springer Nature. ISBN 978-3-030-38021-2.
- ^ https://scikit-learn.org/stable/auto_examples/inspection/plot_permutation_importance.html 31. Aug. 2023
- ^ a b Lin, Yi; Jeon, Yongho (2002). Random forests and adaptive nearest neighbors (Technical report). Technical Report No. 1055. University of Wisconsin. CiteSeerX 10.1.1.153.9168.
- ^ Shi, T.; Horvath, S. (2006). "Unsupervised Learning with Random Forest Predictors". Journal of Computational and Graphical Statistics. 15 (1): 118–138. CiteSeerX 10.1.1.698.2365. doi:10.1198/106186006X94072. JSTOR 27594168. S2CID 245216.
- ^ Shi T, Seligson D, Belldegrun AS, Palotie A, Horvath S (April 2005). "Tumor classification by tissue microarray profiling: random forest clustering applied to renal cell carcinoma". Modern Pathology. 18 (4): 547–57. doi:10.1038/modpathol.3800322. PMID 15529185.
- ^ a b c d e Piryonesi, S. Madeh; El-Diraby, Tamer E. (2021-02-01). "Using Machine Learning to Examine Impact of Type of Performance Indicator on Flexible Pavement Deterioration Modeling". Journal of Infrastructure Systems. 27 (2): 04021005. doi:10.1061/(ASCE)IS.1943-555X.0000602. ISSN 1076-0342. S2CID 233550030.
- ^ Prinzie, A.; Van den Poel, D. (2008). "Random Forests for multiclass classification: Random MultiNomial Logit". Expert Systems with Applications. 34 (3): 1721–1732. doi:10.1016/j.eswa.2007.01.029.
- ^ Prinzie, Anita (2007). "Random Multiclass Classification: Generalizing Random Forests to Random MNL and Random NB". In Roland Wagner; Norman Revell; Günther Pernul (eds.). Database and Expert Systems Applications: 18th International Conference, DEXA 2007, Regensburg, Germany, September 3-7, 2007, Proceedings. Lecture Notes in Computer Science. Vol. 4653. pp. 349–358. doi:10.1007/978-3-540-74469-6_35. ISBN 978-3-540-74467-2.
- ^ a b Smith, Paul F.; Ganesh, Siva; Liu, Ping (2013-10-01). "A comparison of random forest regression and multiple linear regression for prediction in neuroscience". Journal of Neuroscience Methods. 220 (1): 85–91. doi:10.1016/j.jneumeth.2013.08.024. PMID 24012917. S2CID 13195700.
- ^ a b c d Scornet, Erwan (2015). "Random forests and kernel methods". arXiv:1502.03836 [math.ST].
- ^ Breiman, Leo (2000). "Some infinity theory for predictor ensembles". Technical Report 579, Statistics Dept. UCB.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Lin, Yi; Jeon, Yongho (2006). "Random forests and adaptive nearest neighbors". Journal of the American Statistical Association. 101 (474): 578–590. CiteSeerX 10.1.1.153.9168. doi:10.1198/016214505000001230. S2CID 2469856.
- ^ Davies, Alex; Ghahramani, Zoubin (2014). "The Random Forest Kernel and other kernels for big data from random partitions". arXiv:1402.4293 [stat.ML].
- ^ a b Breiman L, Ghahramani Z (2004). "Consistency for a simple model of random forests". Statistical Department, University of California at Berkeley. Technical Report (670). CiteSeerX 10.1.1.618.90.
- ^ a b Arlot S, Genuer R (2014). "Analysis of purely random forests bias". arXiv:1407.3939 [math.ST].
- ^ Sagi, Omer; Rokach, Lior (2020). "Explainable decision forest: Transforming a decision forest into an interpretable tree". Information Fusion. 61: 124–138. doi:10.1016/j.inffus.2020.03.013. S2CID 216444882.
- ^ Vidal, Thibaut; Schiffer, Maximilian (2020). "Born-Again Tree Ensembles". International Conference on Machine Learning. 119. PMLR: 9743–9753. arXiv:2003.11132.
- ^ Piryonesi, Sayed Madeh (November 2019). The Application of Data Analytics to Asset Management: Deterioration and Climate Change Adaptation in Ontario Roads (Doctoral dissertation) (Thesis).
Further reading
[edit]- Prinzie A, Poel D (2007). "Random Multiclass Classification: Generalizing Random Forests to Random MNL and Random NB". Database and Expert Systems Applications. Lecture Notes in Computer Science. Vol. 4653. p. 349. doi:10.1007/978-3-540-74469-6_35. ISBN 978-3-540-74467-2.
- Denisko D, Hoffman MM (February 2018). "Classification and interaction in random forests". Proceedings of the National Academy of Sciences of the United States of America. 115 (8): 1690–1692. Bibcode:2018PNAS..115.1690D. doi:10.1073/pnas.1800256115. PMC 5828645. PMID 29440440.
External links
[edit]- Random Forests classifier description (Leo Breiman's site)
- Liaw, Andy & Wiener, Matthew "Classification and Regression by randomForest" R News (2002) Vol. 2/3 p. 18 (Discussion of the use of the random forest package for R)



























![{\displaystyle [0,1]^{p}\times \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6724c5c806dd7cee08c1f2133fc89f94ed0c2e91)

![{\displaystyle \operatorname {E} [Y^{2}]<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/07a863a618762e9fecf30fadce90c3f6484db196)


![{\displaystyle m(\mathbf {x} )=\operatorname {E} [Y\mid \mathbf {X} =\mathbf {x} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c097ce105048693746d5524ac0ef9fc514da53b)











![{\displaystyle \mathbf {x} \in [0,1]^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/691c9727c059400e1d15031c7e0e08fbd6774282)







![{\displaystyle K_{k}^{cc}(\mathbf {x} ,\mathbf {z} )=\sum _{k_{1},\ldots ,k_{d},\sum _{j=1}^{d}k_{j}=k}{\frac {k!}{k_{1}!\cdots k_{d}!}}\left({\frac {1}{d}}\right)^{k}\prod _{j=1}^{d}\mathbf {1} _{\lceil 2^{k_{j}}x_{j}\rceil =\lceil 2^{k_{j}}z_{j}\rceil },\qquad {\text{ for all }}\mathbf {x} ,\mathbf {z} \in [0,1]^{d}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4b7a16a2bcfb63020d9081379559d5fcd82a7a5)
![{\displaystyle K_{k}^{uf}(\mathbf {0} ,\mathbf {x} )=\sum _{k_{1},\ldots ,k_{d},\sum _{j=1}^{d}k_{j}=k}{\frac {k!}{k_{1}!\ldots k_{d}!}}\left({\frac {1}{d}}\right)^{k}\prod _{m=1}^{d}\left(1-|x_{m}|\sum _{j=0}^{k_{m}-1}{\frac {\left(-\ln |x_{m}|\right)^{j}}{j!}}\right){\text{ for all }}\mathbf {x} \in [0,1]^{d}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e06f4c0b6697dda0b20263456b511570143a7785)




![{\displaystyle \operatorname {E} [N_{n}(\mathbf {x} ,\Theta )]\geq 1,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07f5beb5ef7860bc9f527fb5b01fbed3dc0fc716)
![{\displaystyle \operatorname {P} [a_{n}\leq N_{n}(\mathbf {x} ,\Theta )\leq b_{n}\mid {\mathcal {D}}_{n}]\geq 1-\varepsilon _{n}/2,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bad78155a4139322247009072e48d6b7bf8c5b9)
![{\displaystyle \operatorname {P} [a_{n}\leq \operatorname {E} _{\Theta }[N_{n}(\mathbf {x} ,\Theta )]\leq b_{n}\mid {\mathcal {D}}_{n}]\geq 1-\varepsilon _{n}/2,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71711062ff59f3d2075162074e8f94f917a0cdad)




![{\displaystyle [0,1]^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e13ae4917276744b214714a20b3cb8ee305e309d)





![{\displaystyle \mathbb {E} [{\tilde {m}}_{n}^{cc}(\mathbf {X} )-m(\mathbf {X} )]^{2}\leq C_{1}n^{-1/(3+d\log 2)}(\log n)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbd76dd80031cfdb1b8042faeab38ecaafefa2e3)

![{\displaystyle \mathbb {E} [{\tilde {m}}_{n}^{uf}(\mathbf {X} )-m(\mathbf {X} )]^{2}\leq Cn^{-2/(6+3d\log 2)}(\log n)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51b3c9f4980f936fc01a73621cc56e9857059da4)