Hyperplane separation theorem
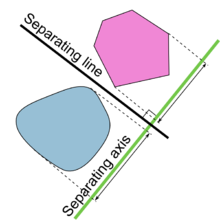 Illustration of the hyperplane separation theorem. | |
| Type | Theorem |
|---|---|
| Field | |
| Conjectured by | Hermann Minkowski |
| Open problem | No |
| Generalizations | Hahn–Banach separation theorem |
In geometry, the hyperplane separation theorem is a theorem about disjoint convex sets in n-dimensional Euclidean space. There are several rather similar versions. In one version of the theorem, if both these sets are closed and at least one of them is compact, then there is a hyperplane in between them and even two parallel hyperplanes in between them separated by a gap. In another version, if both disjoint convex sets are open, then there is a hyperplane in between them, but not necessarily any gap. An axis which is orthogonal to a separating hyperplane is a separating axis, because the orthogonal projections of the convex bodies onto the axis are disjoint.
The hyperplane separation theorem is due to Hermann Minkowski. The Hahn–Banach separation theorem generalizes the result to topological vector spaces.
A related result is the supporting hyperplane theorem.
In the context of support-vector machines, the optimally separating hyperplane or maximum-margin hyperplane is a hyperplane which separates two convex hulls of points and is equidistant from the two.[1][2][3]
Statements and proof
[edit]Hyperplane separation theorem[4] — Let and be two disjoint nonempty convex subsets of . Then there exist a nonzero vector and a real number such that
for all in and in ; i.e., the hyperplane , the normal vector, separates and .
If both sets are closed, and at least one of them is compact, then the separation can be strict, that is, for some
In all cases, assume to be disjoint, nonempty, and convex subsets of . The summary of the results are as follows:
| closed compact | closed | with | |
| closed | closed compact | with | |
| open | |||
| open | open |
The number of dimensions must be finite. In infinite-dimensional spaces there are examples of two closed, convex, disjoint sets which cannot be separated by a closed hyperplane (a hyperplane where a continuous linear functional equals some constant) even in the weak sense where the inequalities are not strict.[5]
Here, the compactness in the hypothesis cannot be relaxed; see an example in the section Counterexamples and uniqueness. This version of the separation theorem does generalize to infinite-dimension; the generalization is more commonly known as the Hahn–Banach separation theorem.
The proof is based on the following lemma:
Lemma — Let and be two disjoint closed subsets of , and assume is compact. Then there exist points and minimizing the distance over and .
Let and be any pair of points, and let . Since is compact, it is contained in some ball centered on ; let the radius of this ball be . Let be the intersection of with a closed ball of radius around . Then is compact and nonempty because it contains . Since the distance function is continuous, there exist points and whose distance is the minimum over all pairs of points in . It remains to show that and in fact have the minimum distance over all pairs of points in . Suppose for contradiction that there exist points and such that . Then in particular, , and by the triangle inequality, . Therefore is contained in , which contradicts the fact that and had minimum distance over .

We first prove the second case. (See the diagram.)
WLOG, is compact. By the lemma, there exist points and of minimum distance to each other. Since and are disjoint, we have . Now, construct two hyperplanes perpendicular to line segment , with across and across . We claim that neither nor enters the space between , and thus the perpendicular hyperplanes to satisfy the requirement of the theorem.
Algebraically, the hyperplanes are defined by the vector , and two constants , such that . Our claim is that and .
Suppose there is some such that , then let be the foot of perpendicular from to the line segment . Since is convex, is inside , and by planar geometry, is closer to than , contradiction. Similar argument applies to .
Now for the first case.
Approach both from the inside by and , such that each is closed and compact, and the unions are the relative interiors . (See relative interior page for details.)
Now by the second case, for each pair there exists some unit vector and real number , such that .
Since the unit sphere is compact, we can take a convergent subsequence, so that . Let . We claim that , thus separating .
Assume not, then there exists some such that , then since , for large enough , we have , contradiction.
Since a separating hyperplane cannot intersect the interiors of open convex sets, we have a corollary:
Separation theorem I — Let and be two disjoint nonempty convex sets. If is open, then there exist a nonzero vector and real number such that
for all in and in . If both sets are open, then there exist a nonzero vector and real number such that
for all in and in .
Case with possible intersections
[edit]If the sets have possible intersections, but their relative interiors are disjoint, then the proof of the first case still applies with no change, thus yielding:
Separation theorem II — Let and be two nonempty convex subsets of with disjoint relative interiors. Then there exist a nonzero vector and a real number such that
in particular, we have the supporting hyperplane theorem.
Supporting hyperplane theorem — if is a convex set in and is a point on the boundary of , then there exists a supporting hyperplane of containing .
If the affine span of is not all of , then extend the affine span to a supporting hyperplane. Else, is disjoint from , so apply the above theorem.
Converse of theorem
[edit]Note that the existence of a hyperplane that only "separates" two convex sets in the weak sense of both inequalities being non-strict obviously does not imply that the two sets are disjoint. Both sets could have points located on the hyperplane.
Counterexamples and uniqueness
[edit]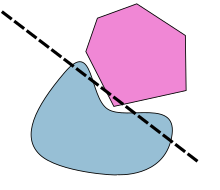
If one of A or B is not convex, then there are many possible counterexamples. For example, A and B could be concentric circles. A more subtle counterexample is one in which A and B are both closed but neither one is compact. For example, if A is a closed half plane and B is bounded by one arm of a hyperbola, then there is no strictly separating hyperplane:
(Although, by an instance of the second theorem, there is a hyperplane that separates their interiors.) Another type of counterexample has A compact and B open. For example, A can be a closed square and B can be an open square that touches A.
In the first version of the theorem, evidently the separating hyperplane is never unique. In the second version, it may or may not be unique. Technically a separating axis is never unique because it can be translated; in the second version of the theorem, a separating axis can be unique up to translation.
The horn angle provides a good counterexample to many hyperplane separations. For example, in , the unit disk is disjoint from the open interval , but the only line separating them contains the entirety of . This shows that if is closed and is relatively open, then there does not necessarily exist a separation that is strict for . However, if is closed polytope then such a separation exists.[6]
More variants
[edit]Farkas' lemma and related results can be understood as hyperplane separation theorems when the convex bodies are defined by finitely many linear inequalities.
More results may be found.[6]
Use in collision detection
[edit]In collision detection, the hyperplane separation theorem is usually used in the following form:
Separating axis theorem — Two closed convex objects are disjoint if there exists a line ("separating axis") onto which the two objects' projections are disjoint.
Regardless of dimensionality, the separating axis is always a line. For example, in 3D, the space is separated by planes, but the separating axis is perpendicular to the separating plane.
The separating axis theorem can be applied for fast collision detection between polygon meshes. Each face's normal or other feature direction is used as a separating axis. Note that this yields possible separating axes, not separating lines/planes.
In 3D, using face normals alone will fail to separate some edge-on-edge non-colliding cases. Additional axes, consisting of the cross-products of pairs of edges, one taken from each object, are required.[7]
For increased efficiency, parallel axes may be calculated as a single axis.
See also
[edit]Notes
[edit]- ^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2008). The Elements of Statistical Learning : Data Mining, Inference, and Prediction (PDF) (Second ed.). New York: Springer. pp. 129–135.
- ^ Witten, Ian H.; Frank, Eibe; Hall, Mark A.; Pal, Christopher J. (2016). Data Mining: Practical Machine Learning Tools and Techniques (Fourth ed.). Morgan Kaufmann. pp. 253–254. ISBN 9780128043578.
- ^ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). Mathematics for Machine Learning. Cambridge University Press. pp. 337–338. ISBN 978-1-108-45514-5.
- ^ Boyd & Vandenberghe 2004, Exercise 2.22.
- ^ Haïm Brezis, Analyse fonctionnelle : théorie et applications, 1983, remarque 4, p. 7.
- ^ a b Stoer, Josef; Witzgall, Christoph (1970). Convexity and Optimization in Finite Dimensions I. Springer Berlin, Heidelberg. (2.12.9). doi:10.1007/978-3-642-46216-0. ISBN 978-3-642-46216-0.
- ^ "Advanced vector math".
References
[edit]- Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (PDF). Cambridge University Press. ISBN 978-0-521-83378-3.
- Golshtein, E. G.; Tretyakov, N.V. (1996). Modified Lagrangians and monotone maps in optimization. New York: Wiley. p. 6. ISBN 0-471-54821-9.
- Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Nondifferentiable and two-level mathematical programming. Boston: Kluwer Academic Publishers. p. 19. ISBN 0-7923-9821-1.
- Soltan, V. (2021). Support and separation properties of convex sets in finite dimension. Extracta Math. Vol. 36, no. 2, 241-278.















































![{\displaystyle [a_{0},b_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2838ee9034d5bf96adfb08ff6cc185c1aee56c18)









![{\displaystyle [a_{0},a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f999eabb0f8a81ac400fc6184c9c4e45c096d406)






















