Tunstall coding
In computer science and information theory, Tunstall coding is a form of entropy coding used for lossless data compression.
History[edit]
Tunstall coding was the subject of Brian Parker Tunstall's PhD thesis in 1967, while at Georgia Institute of Technology. The subject of that thesis was "Synthesis of noiseless compression codes" [1]
Its design is a precursor to Lempel–Ziv.
Properties[edit]
Unlike variable-length codes, which include Huffman and Lempel–Ziv coding, Tunstall coding is a code which maps source symbols to a fixed number of bits.[2]
Both Tunstall codes and Lempel–Ziv codes represent variable-length words by fixed-length codes.[3]
Unlike typical set encoding, Tunstall coding parses a stochastic source with codewords of variable length.
It can be shown[4] that, for a large enough dictionary, the number of bits per source letter can be arbitrarily close to , the entropy of the source.
Algorithm[edit]
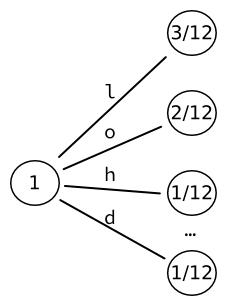
The algorithm requires as input an input alphabet , along with a distribution of probabilities for each word input. It also requires an arbitrary constant , which is an upper bound to the size of the dictionary that it will compute. The dictionary in question, , is constructed as a tree of probabilities, in which each edge is associated to a letter from the input alphabet. The algorithm goes like this:
D := tree of leaves, one for each letter in . While : Convert most probable leaf to tree with leaves.
Example[edit]
This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: wrong probabilities. (August 2014) |
Let's imagine that we wish to encode the string "hello, world". Let's further assume (somewhat unrealistically) that the input alphabet contains only characters from the string "hello, world" — that is, 'h', 'e', 'l', ',', ' ', 'w', 'o', 'r', 'd'. We can therefore compute the probability of each character based on its statistical appearance in the input string. For instance, the letter L appears thrice in a string of 12 characters: its probability is .
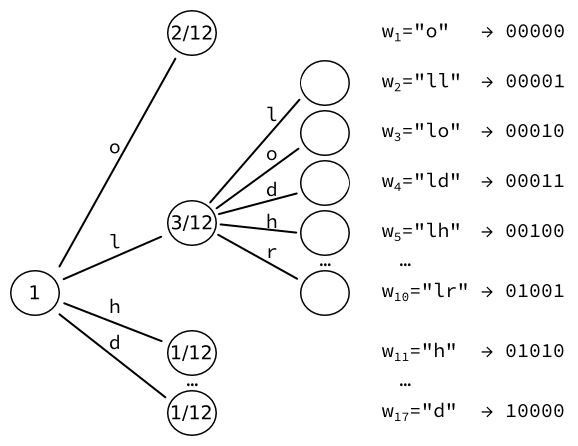
We initialize the tree, starting with a tree of leaves. Each word is therefore directly associated to a letter of the alphabet. The 9 words that we thus obtain can be encoded into a fixed-sized output of bits.
We then take the leaf of highest probability (here, ), and convert it to yet another tree of leaves, one for each character. We re-compute the probabilities of those leaves. For instance, the sequence of two letters L happens once. Given that there are three occurrences of letters followed by an L, the resulting probability is .
We obtain 17 words, which can each be encoded into a fixed-sized output of bits.
Note that we could iterate further, increasing the number of words by every time.
Limitations[edit]
Tunstall coding requires the algorithm to know, prior to the parsing operation, what the distribution of probabilities for each letter of the alphabet is. This issue is shared with Huffman coding.
Its requiring a fixed-length block output makes it lesser than Lempel–Ziv, which has a similar dictionary-based design, but with a variable-sized block output.[clarification needed]
Implied Read for base modification[edit]

This is an example of a Tunstall code being used to read ( for transmit ) any data that is scrambled, e.g. by polynomial scrambling. This particular example helps to modify the base of the data from 2 to 3 in a stream therefore avoiding expensive base modification routines. With base modification we are particularly bound by 'efficiency' of reads, where ideally bits are used at an average to read the code. This ensures that upon use of the new base, which is duty bound to use at best bits per code, our reads do not result in lesser margin of efficiency of transmission for which we are employing the base modification in the first place. We can therefore then employ the read-to-modify-base mechanism for efficiently transmitting the data across channels that have a different base. eg. transmitting binary data across say MLT-3 channels with increased efficiency when compared to mapping codes ( with large number of unused codes ).
| Symbol | Code |
|---|---|
| AA | 010 |
| AB | 011 |
| AC | 100 |
| B | 00 |
| CA | 101 |
| CB | 110 |
| CC | 111 |
We are essentially reading perfectly scrambled binary data or 'implied data' for the purpose of transmitting it using base-3 channels. Please see leaf nodes in the Ternary Tunstall Tree. As we can see, the read will result in the first digit being 'B' - 25% of the time as it has an implied probability of 25%, being of length 2 trying to read from implied data. A 'B' such read does not read any further, but with 75% probability we read 'A' or 'C', requiring another code. Thus the efficiency of the read is 2.75 ( average length of the size 7 Huffman code ) / 1.75 ( average length of the 1 or 2-digit base - 3 Tunstall code ) = which is as per requirement very close to which calculates to an efficiency of . We can then transmit the symbols using base-3 channels efficiently.
References[edit]
- ^ Tunstall, Brian Parker (September 1967). Synthesis of noiseless compression codes. Georgia Institute of Technology.
- ^ http://www.rle.mit.edu/rgallager/documents/notes1.pdf, Study of Tunstall's algorithm at MIT
- ^ "Variable to fixed length adaptive source coding - Lempel-Ziv coding". [1] [2]
- ^ [3], Study of Tunstall's algorithm from EPFL's Information Theory department