2–3–4 tree: Difference between revisions
Davidsawyer1 (talk | contribs) |
Added a link to a book chapter |
||
| Line 81: | Line 81: | ||
* [http://www.cs.unm.edu/~rlpm/499/ttft.html Java Applet showing a 2-3-4 Tree] |
* [http://www.cs.unm.edu/~rlpm/499/ttft.html Java Applet showing a 2-3-4 Tree] |
||
* [http://www.cs.princeton.edu/~rs/talks/LLRB/LLRB.pdf Left-leaning Red-Black Trees - Princeton University, 2008] |
* [http://www.cs.princeton.edu/~rs/talks/LLRB/LLRB.pdf Left-leaning Red-Black Trees - Princeton University, 2008] |
||
* [http://opendatastructures.org/versions/edition-0.1c/ods-java/node47.html Open Data Structures - Section 9.1 - 2-4 Trees ] |
|||
{{CS-Trees}} |
{{CS-Trees}} |
||
Revision as of 13:49, 2 March 2012
In computer science, a 2-3-4 tree (also called a 2-4 tree) is a self-balancing data structure that is commonly used to implement dictionaries. The numbers mean a tree where every node with children (internal node) has either two children (2-node) and one data element or three children (3-node) and two data elements or four children (4-node) and three data elements.
-
2 node
-
3 node
-
4 node
2-3-4 trees are B-trees of order 4; like B-trees in general, they can search, insert and delete in O(log n) time. One property of a 2-3-4 tree is that all external nodes are at the same depth.
2-3-4 trees are an isometry of red-black trees, meaning that they are equivalent data structures. In other words, for every 2-3-4 tree, there exists at least one red-black tree with data elements in the same order. Moreover, insertion and deletion operations on 2-3-4 trees that cause node expansions, splits and merges are equivalent to the color-flipping and rotations in red-black trees. Introductions to red-black trees usually introduce 2-3-4 trees first, because they are conceptually simpler. 2-3-4 trees, however, can be difficult to implement in most programming languages because of the large number of special cases involved in operations on the tree. Red-black trees are simpler to implement [citation needed], so tend to be used instead.
Properties
- Every non-leaf is a 2-node, 3-node or a 4-node. A 2-node contains one data item and has two children. A 3-node contains two data items and has 3 children. A 4-node contains 3 data items and has 4 children.
- All leaves are at the same level (the bottom level)
- All data are kept in sorted order
- Every non-leaf node will contain 1, 2 or 3 fields.
Insertion
To insert a value, we start at the root of the 2-3-4 tree:
- If the current node is a 4-node:
- Remove and save the middle value to get a 3-node.
- Split the remaining 3-node up into a pair of 2-nodes (the now missing middle value is handled in the next step).
- If this is the root node (which thus has no parent):
- the middle value becomes the new root 2-node and the tree height increases by 1. Ascend into the root.
- Otherwise, push the middle value up into the parent node. Ascend into the parent node.
- Find the child whose interval contains the value to be inserted.
- If that child is a leaf, insert the value into current node and finish.
Example
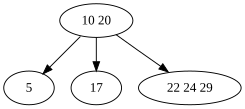
To insert the value "25" into this 2-3-4 tree:
- Begin at the root (10, 20) and descend towards the rightmost child (22, 24, 29). (Its interval (20, ∞) contains 25.)
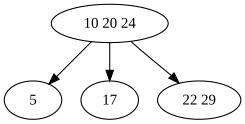
- Node (22, 24, 29) is a 4-node, so its middle element 24 is pushed up into the parent node.
- The remaining 3-node (22, 29) is split into a pair of 2-nodes (22) and (29). Ascend back into the new parent (10, 20, 24).
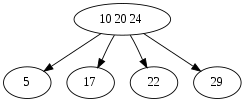
- Descend towards the rightmost child (29). (Its interval (24, ∞) contains 25.)
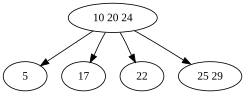
- Node (29) has no leftmost child. (The child for interval (∞, 29) is empty.) Stop here and insert value 25 into this node.
Deletion
Consider just leaving the element there, marking it “deleted,” possibly to be re-used for a future insertion.
Find the element to be deleted. If the element is not in a leaf node remember its location and continue searching until a leaf, which will contain the element’s successor, is reached. Then swap the leaf element with the one to be deleted, and delete the element node. It is simplest to make adjustments to the tree from the top down, as the element to be deleted is pursued that guarantee that the leaf node found is not a two-node, so that we can delete something from it and leave it there.
The adjustments we make on the way to a leaf are as follows: Assume, without loss of generality, that the child we are about to go to is the leftmost.
If we're at the root
If the root and both children are two-nodes, combine all three elements into the root, making a 4-node and shortening the tree,
Otherwise, if the root and left child are two-nodes, the right child isn't a two-node. Perform a left rotation to make the left
sibling a 3-node, and move to the left child.
From now on, we can be sure that we're at a node which is not a 2-node.
If the leftmost child is not a 2-node, just move to it. If the adjacent sibling is not a 2-node, perform a left rotation using its leftmost element to make the left child a 3-node. Otherwise, add the leftmost element of the parent and the single element of the sibling to the left node, making it a 4-node, and discard the empty sibling. Go to the left-most child.
Deletion in a 2-3-4 tree is O(log n), assuming transfer and fusion run in constant time ( O(1) ).[1][3]
See also
References
- ^ a b Ford, William; Topp, William (2002), Data Structures with C++ Using STL (2nd ed.), New Jersey: Prentice Hall, p. 683, ISBN 0-13-085850-1
- ^ Goodrich, Michael T; Tamassia, Roberto; Mount, David M (2002), Data Structures and Algorithms in C++, Wiley, ISBN 0-471-20208-8
- ^ Grama, Ananth (2004). "(2,4) Trees" (PDF). CS251: Data Structures Lecture Notes. Department of Computer Science, Purdue University. Retrieved 2008-04-10.