Template:X8: Difference between revisions

Content deleted Content added

Inline

Revision as of 05:00, 19 October 2010

This sandbox is itself a template. This sandbox is for experimenting with templates.

Welcome to Template:X8, a Wikipedia template sandbox. This page is itself a template, and it allows you to carry out experiments related to template editing. If you wish to experiment with article editing, use the Wikipedia Sandbox or your own user sandbox.

To edit, click the edit tab above, make your changes and click the Publish changes button when finished. Content will not stay permanently; the template sandboxes are automatically cleaned every twelve hours.

Please do not place copyrighted, offensive, illegal or libelous content in the sandboxes. For assistance with template coding, try the technical forum at the Village Pump.

You can also try Special:ExpandTemplates and several other template sandboxes that you can use to carry out experiments.

If you need more sandboxes, please consider using testwiki. You can also conduct tests using the Wikipedia Sandbox. For instance, to transclude this template there, edit it so that it includes: {{X8}}

The octonions: a non-technical introduction Keywords: quaternion, FFT

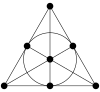
In this article, we try to understand the octonions. You can think of them as 2 quaternions welded together. This is like a marriage. In fact, the wedding band at the right is a Mobius Band. Its just like the inner triangle (represented by a circle) and the outer triangle.

Action principle

Perhaps the most important law of nature is the action principle. Action is a pattern, times its FFT: Energy*time, position*momentum, and so on. The units are those of Plancks constant. When people learned about 4 dimensional spacetime, the action principle stayed the same, but now there were 4 dimensions: energy-momentum * spacetime, and so on.

If nature is 3+1 dimensional, then its important to use a 3+1 dimensional algebra. You can think of the sun. It could rotate in any of the three directions. The magnetic field is symmetric above and below the equator, and it oscillates.

The hydrogen atom is a bit like that. Its the simplest element, and the most abundant in the cosmos. Its a dot, with a dot going around it. The dots have opposite charge, so its stable. There is an article where they express the resonances of the 3-sphere with quaternions.^[1].

A guitar string has lots of resonances. You can think of the 3-sphere as a rotated 3-d guitar string. There are also lots of resonances of the 3-sphere. One of them uses the golden ratio. Its called the 600-cell, and its the same as the 2x2 matrices (of determinant one) over the integers mod 5. Its closely related to the energy levels of hydrogen.

Relativity

left|130pxSome people dont like the theory of relativity. Its too hard. Fortunately, there's a way out. In the 1960's, someone introduced the Regge Calculus. You divide spacetime into 4-d tetrahedrons, and make the them smaller and smaller. It works. Recently, Miller and McDonald wrote a paper on a welding together of the spacetime and its fourier transform^[2]. They dont say thats what it is, but thats what it is. You can think of 2 4-d tetrahedrons welded together. They showed that it gives improved results. Thats just like the picture at the top of this article. There are 2 tetrahedrons welded together (or triangles if you like). Again we have the action principle.

This is where the octonions come in. Some people think that the octonions dont include a fourier transform, but they do. If you look at the multiplication table, you can see it consists of 4 block matrices. The 4 diagonals are just like complex numbers, and the 4 off-diagonals are just like a 2x2 Hadamard matrix. Its hard to explain. But the important thing is this: a Hadamard matrix is a 2x2 FFT. This says the action principle is already included in the octonions.

You can even define quantum mechanics with octonions. But there is a question about whether you can define Hilbert spaces with them. A Hilbert space is like the overtones of a guitar string. Some people say you can't, while other people say you can.^[3]^[4]. But it was a construction that people invented before they understood quantum mechanics more completely, so its not incredibly vital.

References

^ Lachieze-Rey Marc, Laplacian eigenmodes for the three-Sphere, arXiv:math/0401153
^ Jonathan R. McDonald, Warner A. Miller: The Fundamental Role of Dual Tessellations in Regge Calculus, arXiv:0804.0279
^ Stefano De Leo, Octonionic Dirac Equation, arXiv:hep-th/9609033
^ Stefano De Leo, Octonionic Quantum Mechanics and Complex Geometry, arXiv:hep-th/9609032v1

[1] Lachieze-Rey Marc, Laplacian eigenmodes for the three-Sphere, arXiv:math/0401153

[2] Jonathan R. McDonald, Warner A. Miller: The Fundamental Role of Dual Tessellations in Regge Calculus, arXiv:0804.0279

[3] Stefano De Leo, Octonionic Dirac Equation, arXiv:hep-th/9609033

[4] Stefano De Leo, Octonionic Quantum Mechanics and Complex Geometry, arXiv:hep-th/9609032v1

[1]

[2]

[3]

[4]

@@ Line 25: / Line 25: @@
 ;Relativity
-[[Image:Escher Circle Limit III.jpg|left|130px]]Some people dont like the theory of relativity.  Its too hard.  Fortunately, there's a way out.  In the 1960's, someone introduced the [[Regge Calculus]].  You divide spacetime into 4-d [[tetrahedron]]s, and make the them smaller and smaller.  It works.  Recently, Miller and McDonald wrote a paper on a welding together of the spacetime and its fourier transform<ref>Jonathan R. McDonald, Warner A. Miller: ''The Fundamental Role of Dual Tessellations in Regge Calculus'',  arXiv:0804.0279</ref>.  They dont say thats what it is, but thats what it is.  You can think of 2 4-d tetrahedrons welded together.  They showed that it gives improved results.  Thats just like the picture at the top of this article.  There are 2 tetrahedrons welded together (or triangles if you like).   Again we have the action principle.
+[[:Image:Escher Circle Limit III.jpg|left|130px]]<!--Non free file removed by DASHBot-->Some people dont like the theory of relativity.  Its too hard.  Fortunately, there's a way out.  In the 1960's, someone introduced the [[Regge Calculus]].  You divide spacetime into 4-d [[tetrahedron]]s, and make the them smaller and smaller.  It works.  Recently, Miller and McDonald wrote a paper on a welding together of the spacetime and its fourier transform<ref>Jonathan R. McDonald, Warner A. Miller: ''The Fundamental Role of Dual Tessellations in Regge Calculus'',  arXiv:0804.0279</ref>.  They dont say thats what it is, but thats what it is.  You can think of 2 4-d tetrahedrons welded together.  They showed that it gives improved results.  Thats just like the picture at the top of this article.  There are 2 tetrahedrons welded together (or triangles if you like).   Again we have the action principle.
 This is where the [[octonion]]s come in.  Some people think that the octonions dont include a fourier transform, but they do.  If you look at the multiplication table, you can see it consists of 4 block matrices.  The 4 diagonals are just like complex numbers, and the 4 off-diagonals are just like a 2x2 [[Hadamard matrix]].  Its hard to explain.  But the important thing is this: a Hadamard matrix is a 2x2 FFT.  This says the action principle is already included in the octonions.