Lotka–Volterra equations

The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order, non-linear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one a predator and one its prey. They were proposed independently by Alfred J. Lotka in 1925 and Vito Volterra in 1926.

${\frac {dx}{dt}}=x(\alpha -\beta y)$

${\frac {dy}{dt}}=-y(\gamma -\delta x)$

where

• $y$ is the number of some predator (for example, wolves);
• $x$ is the number of its prey (for example, rabbits);
• ${\frac {dy}{dt}}$ and ${\frac {dx}{dt}}$ represents the growth of the two populations against time;
• $t$ represents the time; and
• $\alpha$, $\beta$, $\gamma$ and $\delta$ are parameters representing the interaction of the two species.

Physical meanings of the equations

When multiplied out, the equations take a form useful for physical interpretation. Their origin should be considered from a more general framework,

${\frac {dx}{dt}}=f(x,y)x$

${\frac {dy}{dt}}=g(x,y)y$

where both functions represent per capita growth rates of the prey and predator, respectively. These functions are too general, so a Taylor series approximation is performed to obtain linearized per capita rates,

$f(x,y)=A_{0}-A_{1}x-A_{2}y\,$

$g(x,y)=B_{0}+B_{1}x-B_{2}y\,$

The signs of the coefficients arise from assumptions of population regulation, and by choosing nonzero coefficients appropriately, an ecologist can obtain predator-prey, competition, disease, and mutualism models that provide general insight into ecological systems.

ASSUMPTIONS 1) the prey population finds ample food at all times. 2) the food supply of the predator population depends entirely on the prey populations. 3) the rate of change of population is proportional to its size. 4) During the process, the environment does not change in favor of one species and the genetic adaptation is sufficiently slow.

Prey

The prey equation becomes:

${\frac {dx}{dt}}=\alpha x-\beta xy.$

The prey are assumed to have an unlimited food supply, and to reproduce exponentially unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet; this is represented above by βxy. If either x or y is zero then there can be no predation.

With these two terms the equation above can be interpreted as: the change in the prey's numbers is given by its own growth minus the rate at which it is preyed upon.

Predators

The predator equation becomes:

${\frac {dy}{dt}}=\delta xy-\gamma y.$

In this equation, δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). γy represents the natural death of the predators; it leads to an exponential decay in the absence of prey.

Hence the equation expresses the change in the predator population as growth fueled by the food supply, minus natural death.

Solutions to the equations

The equations have periodic solutions which do not have a simple expression in terms of the usual trigonometric functions. However, an approximate linearised solution yields a simple harmonic motion with the population of predators following that of prey by 90°.

An example problem

Suppose there are two species of animals, a baboon (prey) and a cheetah (predator). If the initial conditions are 80 baboons and 40 cheetahs, one can plot the progression of the two species over time. Time is dimensionless.

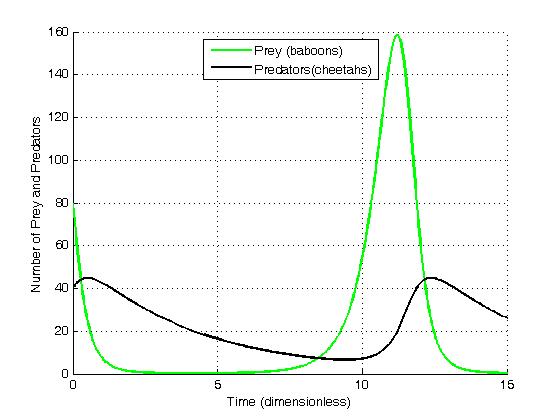
One can also plot a solution which corresponds to the oscillatory nature of the population of the two species. At any given time, the solution is somewhere on the inside of these elliptical solutions.

These graphs clearly illustrate a serious problem with this as a biological model: in each cycle, the baboon population is reduced to extremely low numbers yet recovers (while the cheetah population remains sizeable at the lowest baboon density). Given chance fluctuations, discrete numbers of individuals, and the family structure and lifecycle of baboons, the baboons actually go extinct and by consequence the cheetahs as well. This modelling problem has been called the "atto-fox problem", an atto-fox being an imaginary 10⁻¹⁸ of a fox, in relation to rabies modelling in the UK.

Dynamics of the system

In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low the prey population will increase again. These dynamics continue in a cycle of growth and decline.

Population equilibrium

Population equilibrium occurs in the model when neither of the population levels is changing, i.e. when both of the derivatives are equal to 0.

$x(\alpha -\beta y)=0\,$

$-y(\gamma -\delta x)=0\,$

When solved for x and y the above system of equations yields

$\left\{y=0,x=0\right\}\,$

and

$\left\{y={\frac {\alpha }{\beta }},x={\frac {\gamma }{\delta }}\right\},\,$

hence there are two equilibria.

The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters, α, β, γ, and δ.

Stability of the fixed points

The stability of the fixed point at the origin can be determined by performing a linearization using partial derivatives, while the other fixed point requires a slightly more sophisticated method.

The Jacobian matrix of the predator-prey model is

$J(x,y)={\begin{bmatrix}\alpha -\beta y&-\beta x\\\delta y&\delta x-\gamma \\\end{bmatrix}}$

First fixed point

When evaluated at the steady state of (0, 0) the Jacobian matrix J becomes

$J(0,0)={\begin{bmatrix}\alpha &0\\0&-\gamma \\\end{bmatrix}}$

The eigenvalues of this matrix are

$\lambda _{1}=\alpha ,\quad \lambda _{2}=-\gamma .\,$

In the model α and γ are always greater than zero, and as such the sign of the eigenvalues above will always differ. Hence the fixed point at the origin is a saddle point.

The stability of this fixed point is of importance. If it were stable, non-zero populations might be attracted towards it, and as such the dynamics of the system might lead towards the extinction of both species for many cases of initial population levels. However, as the fixed point at the origin is a saddle point, and hence unstable, we find that the extinction of both species is difficult in the model. (In fact, this can only occur if the prey are artificially completely eradicated, causing the predators to die of starvation. If the predators are eradicated, the prey population grows without bound in this simple model).

Second fixed point

Evaluating J at the second fixed point we get

$J\left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)={\begin{bmatrix}0&-{\frac {\beta \gamma }{\delta }}\\{\frac {\alpha \delta }{\beta }}&0\\\end{bmatrix}}.$

The eigenvalues of this matrix are

$\lambda _{1}=i{\sqrt {\alpha \gamma }},\quad \lambda _{2}=-i{\sqrt {\alpha \gamma }}.\,$

As the eigenvalues are both purely imaginary, this fixed point is not hyperbolic, so no conclusions can be drawn from the linear analysis. However, the system admits a constant of motion

$K=y^{\alpha }e^{-\beta y}\,x^{\gamma }e^{-\delta x},$

and the level curves $K={\mbox{const}}$ are closed trajectories surrounding the fixed point. Consequently, the levels of the predator and prey populations cycle, and oscillate around this fixed point.

The largest value of the constant $K$ can be obtained by solving the optimization problem

$y^{\alpha }e^{-\beta y}\,x^{\gamma }e^{-\delta x}={\frac {y^{\alpha }x^{\gamma }}{e^{\delta x+\beta y}}}\longrightarrow \max \limits _{x,y>0}$

The maximal value of $K$ is attained at the stationary point $\left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)$ and it is given by

$K^{*}=\left({\frac {\alpha }{\beta e}}\right)^{\alpha }\left({\frac {\gamma }{\delta e}}\right)^{\gamma },$

where $e$ is the Euler's Number.

See also

• Lotka–Volterra inter-specific competition equations
• Population dynamics
• Nicholson–Bailey model

References

• E. R. Leigh (1968) The ecological role of Volterra's equations, in Some Mathematical Problems in Biology – a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.
• Understanding Nonlinear Dynamics. Daniel Kaplan and Leon Glass.
• J.D. Murray. Mathematical Biology I: An Introduction. Springer-Verlag, 2003
• V. Volterra. Variations and fluctuations of the number of individuals in animal species living together. In Animal Ecology. McGraw–Hill, 1931. Translated from 1928 edition by R. N. Chapman.

External links

• Lotka–Volterra Predator-Prey Model by Elmer G. Wiens
• Lotka-Volterra Model
• [1] NANIA Lotka-Volterra applet