Kepler orbit

For further closely relevant mathematical developments see also Two-body problem, also Gravitational two-body problem, and Kepler problem

In celestial mechanics, a Kepler orbit describes the motion of an orbiting body as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. (A Kepler orbit can also form a straight line.) It considers only the gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non-spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways.

In most applications, there is a large central body, the center of mass of which is assumed to be the center of mass of the entire system. By decomposition, the orbits of two objects of similar mass can be described as Kepler orbits around their common center of mass, their barycenter.

History and relationship with Newton's Laws

The mechanisms of Newton's law of universal gravitation; a point mass m₁ attracts another point mass m₂ by a force F₂ which is proportional to the product of the two masses and inversely proportional to the square of the distance (r) between them. Regardless of masses or distance, the magnitudes of |F₁| and |F₂| will always be equal. G is the gravitational constant.

Johannes Kepler developed his laws of planetary motion around 1605, from astronomical tables detailing the movements of the visible planets. Kepler's First Law is:

"The orbit of every planet is an ellipse with the sun at a focus."

The mathematics of ellipses are thus the mathematics of Kepler orbits, later expanded to include parabolas and hyperbolas.

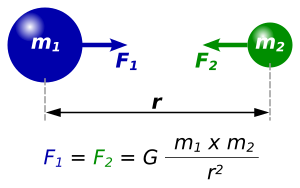
Isaac Newton published his law of universal gravitation in 1687, which says:

Every point mass attracts every other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between the point masses:

$F=G{\frac {m_{1}m_{2}}{r^{2}}},$

where:

• F is the magnitude of the gravitational force between the two point masses,
• G is the gravitational constant,
• m₁ is the mass of the first point mass,
• m₂ is the mass of the second point mass,
• r is the distance between the two point masses.

The shapes of large celestial bodies are close to spheres. By symmetry, the net gravitational force attracting a mass point towards a homogeneous sphere must be directed towards the centre of the sphere. The shell theorem (also proven by Isaac Newton) says that the magnitude of this force is the same as if all mass was concentrated in the middle of the sphere, even if the density of the sphere varies with depth (as it does for most celestial bodies). From this immediately follows that the attraction between two homogeneous spheres is as if both had its mass concentrated to its center.

Smaller objects, like asteroids or spacecraft often have a shape strongly deviating from a sphere. But the gravitational forces produced by these irregularities are generally small compared to the gravity of the central body. The difference between an irregular shape and a perfect sphere also diminishes with distances, and most orbital distances are very large when compared with the diameter of a small orbiting body. Thus for some applications, shape irregularity can be neglected without significant impact on accuracy.

Planets that rotate (such as the Earth) take a slightly oblate shape because of the centrifugal force and with such an oblate shape the gravitational attraction will deviate somewhat from that of a homogeneous sphere. This phenomenon is quite noticeable for artificial Earth satellites, especially those in low orbits, but at a large distance the effect of this oblateness is very small and the planetary motions in the Solar System can be computed with sufficient precision assuming the gravitational attraction between any two bodies of the Solar System follow the law:

$F=G{\frac {m_{1}m_{2}}{r^{2}}},$

where r is the distance between the centres of the celestial bodies.

The two-body problem is the case that there are only two point masses (or homogeneous spheres).

If the two mass points (or homogenous spheres) have the masses $m_{1}$ and $m_{2}$ and the position vectors ${\bar {r}}_{1}$ and ${\bar {r}}_{2}$ relative a point fixed with respect to inertial space (for example relative their common centre of mass) the equations of motion for the two mass points are

$m_{1}\cdot {\ddot {{\bar {r}}_{1}}}=-G{\frac {m_{1}m_{2}}{r^{2}}}\cdot {\hat {r}}$

$m_{2}\cdot {\ddot {{\bar {r}}_{2}}}=G{\frac {m_{1}m_{2}}{r^{2}}}\cdot {\hat {r}}$

where

$r=|{\bar {r}}_{1}-{\bar {r}}_{2}|$

is the distance between the bodies

and

${\hat {r}}={\frac {{\bar {r}}_{1}-{\bar {r}}_{2}}{r}}$

is the unit vector pointing from body 2 to body 1.

Dividing with the factors $m_{1}$ and $m_{2}$and subtracting the resulting equations one gets the differential equation

${\ddot {\bar {r}}}=-Gm\cdot {\frac {\hat {r}}{r^{2}}}\ \ (1)$

for the vector from body 2 to body 1

${\bar {r}}={\bar {r}}_{1}-{\bar {r}}_{2}$

This differential equation for the two body case can be completely solved mathematically and the resulting orbit which follows Kepler's laws of planetary motion is called a "Kepler orbit". The orbits of all planets are to high accuracy Kepler orbits around the Sun (as observed by Johannes Kepler!), the small deviations being due to the much weaker gravitational attractions between the planets, or in the case of Mercury, due to general relativity. Also the orbits around the Earth of the Moon and of the artificial satellites are with a fair approximation Kepler orbits. In fact, the gravitational acceleration towards the Sun is about the same for the Earth and the satellite and therefore in a first approximation "cancels out". Also in high accuracy applications for which the equation of motion must be integrated numerically with all gravitational and non-gravitational forces (such as solar radiation pressure and atmospheric drag) being taken into account, the Kepler orbit concepts are of paramount importance and heavily used.

For example, the orbital elements:

• Semi-major axis
• eccentricity
• Inclination
• Longitude of the ascending node
• Argument of periapsis
• True anomaly

are only defined for a Kepler orbit. The use of orbital elements therefore always implies that the orbit is approximated with the Kepler orbit having these orbital elements.

Mathematical solution of the differential equation (1) above

Like for the movement under any central force, i.e. a force aligned with ${\hat {r}}$, the specific relative angular momentum ${\bar {H}}={\bar {r}}\times {\dot {\bar {r}}}$ stays constant:

${\dot {\bar {H}}}={\dot {\overbrace {{\bar {r}}\times {\dot {\bar {r}}}} }}={\dot {\bar {r}}}\times {\dot {\bar {r}}}+{\bar {r}}\times {\ddot {\bar {r}}}={\bar {0}}+{\bar {0}}={\bar {0}}$

Introducing a coordinate system ${\hat {x}}\ ,\ {\hat {y}}$ in the plane orthogonal to ${\bar {H}}$ and polar coordinates

${\bar {r}}=r\cdot (\cos \theta \cdot {\hat {x}}+\sin \theta \cdot {\hat {y}})$

the differential equation (1) takes the form (see "Polar coordinates#Vector calculus")

$r^{2}\cdot {\dot {\theta }}=H\ \ (2)$

${\ddot {r}}-r\cdot {\dot {\theta }}^{2}=-{\frac {\mu }{r^{2}}}\ \ (3)$

Taking the time derivative of (2) one gets

${\ddot {\theta }}=-{\frac {2\cdot H\cdot {\dot {r}}}{r^{3}}}\ \ (4)$

Using the chain rule for differentiation one gets

${\dot {r}}={\frac {dr}{d\theta }}\cdot {\dot {\theta }}\ \ (5)$

${\ddot {r}}={\frac {d^{2}r}{d\theta ^{2}}}\cdot {\dot {\theta }}^{2}+{\frac {dr}{d\theta }}\cdot {\ddot {\theta }}\ \ (6)$

Using the expressions for ${\dot {\theta }},\ {\ddot {\theta }},\ {\dot {r}},\ {\ddot {r}}$ of equations (2), (4), (5) and (6) all time derivatives in (3) can be replaced by derivatives of r as function of $\theta$. After some simplification one gets

${\ddot {r}}-r\cdot {\dot {\theta }}^{2}={\frac {H^{2}}{r^{4}}}\cdot \left({\frac {d^{2}r}{d\theta ^{2}}}-2\cdot {\frac {\left({\frac {dr}{d\theta }}\right)^{2}}{r}}-r\right)=-{\frac {\mu }{r^{2}}}\ \ (7)$

The differential equation (7) can be solved analytically by the variable substitution

$r={\frac {1}{s}}\ \ (8)$

Using the chain rule for differentiation one gets:

${\frac {dr}{d\theta }}=-{\frac {1}{s^{2}}}\cdot {\frac {ds}{d\theta }}\ \ (9)$

${\frac {d^{2}r}{d\theta ^{2}}}={\frac {2}{s^{3}}}\cdot \left({\frac {ds}{d\theta }}\right)^{2}-{\frac {1}{s^{2}}}\cdot {\frac {d^{2}s}{d\theta ^{2}}}\ \ (10)$

Using the expressions (10) and (9) for ${\frac {d^{2}r}{d\theta ^{2}}}$ and ${\frac {dr}{d\theta }}$ one gets

$H^{2}\cdot \left({\frac {d^{2}s}{d\theta ^{2}}}+s\right)=\mu \ \ (11)$

with the general solution

$s={\frac {\mu }{H^{2}}}\cdot \left(1+e\cdot \cos(\theta -\theta _{0})\right)\ \ (12)$

where e and $\theta _{0}$ are constants of integration depending on the initial values for s and ${\frac {ds}{d\theta }}$.

Instead of using the constant of integration $\theta _{0}$ explicitly one introduces the convention that the unit vectors ${\hat {x}}\ ,\ {\hat {y}}$ defining the coordinate system in the orbital plane are selected such that $\theta _{0}$ takes the value zero and e is positive. This then means that $\theta$ is zero at the point where $s$ is maximal and therefore $r={\frac {1}{s}}$ is minimal. Defining the parameter p as ${\frac {H^{2}}{\mu }}$ one has that

$r={\frac {1}{s}}={\frac {p}{1+e\cdot \cos \theta }}\ \ (13)$

This is the equation in polar coordinates for a conic section with origin in a focal point. The argument $\theta$ is called "true anomaly".

For $e=0$ this is a circle with radius p.

For $0<e<1$ this is an ellipse with

$a={\frac {p}{1-e^{2}}}\ \ (14)$

$b={\frac {p}{\sqrt {1-e^{2}}}}=a\cdot {\sqrt {1-e^{2}}}\ \ (15)$.

For $e=1$ this is a parabola with focal length ${\frac {p}{2}}$

For $e>1$ this is a hyperbola with

$a={\frac {p}{e^{2}-1}}\ \ (16)$

$b={\frac {p}{\sqrt {e^{2}-1}}}=a\cdot {\sqrt {e^{2}-1}}\ \ (17)$

The following image illustrates an ellipse (red), a parabola (green) and a hyperbola (blue)

The lower branch of the hyperbola is irrelevant here (image from Wikimedia Commons).

The point below the focal point F is the point with $\theta =0$ for which the distance to the focus takes the minimal value ${\frac {p}{1+e}}$, the pericentre. For the ellipse there is also an apocentre for which the distance to the focus takes the maximal value ${\frac {p}{1-e}}$. For the hyperbola the range for $\theta$ is

$\left[-\cos ^{-1}(-{\frac {1}{e}})<\theta <\cos ^{-1}(-{\frac {1}{e}})\right]$

and for a parobola the range is

$\left[-\pi <\theta <\pi \right]$

Using the chain rule for differentiation (5), the equation (2) and the definition of p as ${\frac {H^{2}}{\mu }}$ one gets that the radial velocity component is

$V_{r}={\dot {r}}={\frac {H}{p}}\cdot e\cdot \sin \theta ={\sqrt {\frac {\mu }{p}}}\cdot e\cdot \sin \theta \ \ (18)$

and that the tangential component is

$V_{t}=r\cdot {\dot {\theta }}={\frac {H}{r}}={\sqrt {\frac {\mu }{p}}}\cdot (1+e\cdot \cos \theta )\ \ (19)$

The connection between the polar argument $\theta$ and time t is slightly different for elliptic and hyperbolic orbits.

For an elliptic orbit one switches to the "eccentric anomaly" E for which

$x=a\cdot (\cos E-e)\ \ (20)$

$y=b\cdot \sin E\ \ (21)$

and consequently

${\dot {x}}=-a\cdot \sin E\cdot {\dot {E}}\ \ (22)$

${\dot {y}}=b\cdot \cos E\cdot {\dot {E}}\ \ (23)$

and the angular momentum H is

$H=x\cdot {\dot {y}}-y\cdot {\dot {x}}=a\cdot b\cdot (1-e\cdot \cos E)\cdot {\dot {E}}\ \ (24)$

Integrating with respect to time t one gets

$H\cdot t=a\cdot b\cdot (E-e\cdot \sin E)\ \ (25)$

under the assumption that time $t=0$ is selected such that the integration constant is zero.

As by definition of p one has

$H={\sqrt {\mu \cdot p}}\ \ (26)$

this can be written

$t=a\cdot {\sqrt {\frac {a}{\mu }}}(E-e\cdot \sin E)\ \ (27)$

For a hyperbolic orbit one uses the hyperbolic functions for the parameterisation

$x=a\cdot (e-\cosh E)\ \ (28)$

$y=b\cdot \sinh E\ \ (29)$

for which one has

${\dot {x}}=-a\cdot \sinh E\cdot {\dot {E}}\ \ (30)$

${\dot {y}}=b\cdot \cosh E\cdot {\dot {E}}\ \ (31)$

and the angular momentum H is

$H=x\cdot {\dot {y}}-y\cdot {\dot {x}}=a\cdot b\cdot (e\cdot \cosh E-1)\cdot {\dot {E}}\ \ (32)$

Integrating with respect to time t one gets

$H\cdot t=a\cdot b\cdot (e\cdot \sinh E-E)\ \ (33)$

i.e.

$t=a\cdot {\sqrt {\frac {a}{\mu }}}(e\cdot \sinh E-E)\ \ (34)$

To find what time t that corresponds to a certain true anomaly $\theta$ one computes corresponding parameter E connected to time with relation (27) for an elliptic and with relation (34) for a hyperbolic orbit.

Note that the relations (27) and (34) define a mapping between the ranges

$\left[-\infty <t<\infty \right]\longleftrightarrow \left[-\infty <E<\infty \right]$

Some additional formulae

See also Equation of the center – Analytical expansions

For an elliptic orbit one gets from (20) and (21) that

$r=a\cdot (1-e\cdot \cos E)\ \ (35)$

and therefore that

$\cos \theta ={\frac {x}{r}}={\frac {\cos E-e}{1-e\cdot \cos E}}\ \ (36)$

From (36) then follows that

$\tan ^{2}{\frac {\theta }{2}}={\frac {1-\cos \theta }{1+\cos \theta }}={\frac {1-{\frac {\cos E-e}{1-e\cdot \cos E}}}{1+{\frac {\cos E-e}{1-e\cdot \cos E}}}}={\frac {1-e\cdot \cos E-\cos E+e}{1-e\cdot \cos E+\cos E-e}}={\frac {1+e}{1-e}}\ \cdot \ {\frac {1-\cos E}{1+\cos E}}={\frac {1+e}{1-e}}\ \cdot \ \tan ^{2}{\frac {E}{2}}$

From the geometrical construction defining the eccentric anomaly it is clear that the vectors $(\ \cos E\ ,\ \sin E\ )$ and $(\ \cos \theta \ ,\ \sin \theta \ )$ are on the same side of the x-axis. From this then follows that the vectors $(\ \cos {\frac {E}{2}}\ ,\ \sin {\frac {E}{2}}\ )$ and $(\ \cos {\frac {\theta }{2}}\ ,\ \sin {\frac {\theta }{2}}\ )$ are in the same quadrant. One therefore has that

$\tan {\frac {\theta }{2}}={\sqrt {\frac {1+e}{1-e}}}\cdot \tan {\frac {E}{2}}\ \ (37)$

and that

$\theta =2\cdot \operatorname {arg} ({\sqrt {1-e}}\ \cdot \ \cos {\frac {E}{2}}\ ,\ {\sqrt {1+e}}\ \cdot \ \sin {\frac {E}{2}})+n\cdot 2\pi \ \ (38)$.

$E=2\cdot \operatorname {arg} ({\sqrt {1+e}}\ \cdot \ \cos {\frac {\theta }{2}}\ ,\ {\sqrt {1-e}}\ \cdot \ \sin {\frac {\theta }{2}})+n\cdot 2\pi \ \ (39)$

where "$\operatorname {arg} (x\ ,\ y)$" is the polar argument of the vector $(\ x\ ,\ y\ )$ and n is selected such that $\left|E-\theta \right|<\pi$

For the numerical computation of $\operatorname {arg} (x\ ,\ y)$ the standard function ATAN2(y,x) (or in double precision DATAN2(y,x)) available in for example the programming language FORTRAN can be used.

Note that this is a mapping between the ranges

$\left[-\infty <\theta <\infty \right]\longleftrightarrow \left[-\infty <E<\infty \right]$

For an hyperbolic orbit one gets from (28) and (29) that

$r=a\cdot (e\cdot \cosh E-1)\ \ (40)$

and therefore that

$\cos \theta ={\frac {x}{r}}={\frac {e-\cosh E}{e\cdot \cosh E-1}}\ \ (41)$

As

$\tan ^{2}{\frac {\theta }{2}}={\frac {1-\cos \theta }{1+\cos \theta }}={\frac {1-{\frac {e-\cosh E}{e\cdot \cosh E-1}}}{1+{\frac {e-\cosh E}{e\cdot \cosh E-1}}}}={\frac {e\cdot \cosh E-e+\cosh E}{e\cdot \cosh E+e-\cosh E}}={\frac {e+1}{e-1}}\ \cdot \ {\frac {\cosh E-1}{\cosh E+1}}={\frac {e+1}{e-1}}\ \cdot \ \tanh ^{2}{\frac {E}{2}}$

and as $\tan {\frac {\theta }{2}}$ and $\tanh {\frac {E}{2}}$ have the same sign it follows that

$\tan {\frac {\theta }{2}}={\sqrt {\frac {e+1}{e-1}}}\cdot \tanh {\frac {E}{2}}\ \ (42)$

This relation is convenient for passing between "true anomaly" and the parameter E, the latter being connected to time through relation (34). Note that this is a mapping between the ranges

$\left[-\cos ^{-1}(-{\frac {1}{e}})<\theta <\cos ^{-1}(-{\frac {1}{e}})\right]\longleftrightarrow \left[-\infty <E<\infty \right]$

and that ${\frac {E}{2}}$ can be computed using the relation

$\tanh ^{-1}x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)$

From relation (27) follows that the orbital period P for an elliptic orbit is

$P=2\pi \cdot a\cdot {\sqrt {\frac {a}{\mu }}}\ \ (43)$

As the potential energy corresponding to the force field of relation (1) is

$-{\frac {\mu }{r}}$

it follows from (13) , (14), (18) and (19) that the sum of the kinetic and the

potential energy

${\frac {{V_{r}}^{2}+{V_{t}}^{2}}{2}}-{\frac {\mu }{r}}$

for an elliptic orbit is

$-{\frac {\mu }{2\cdot a}}\ \ (44)$

and from (13) , (16), (18) and (19) that the sum of the kinetic and the

potential energy for a hyperbolic orbit is

${\frac {\mu }{2\cdot a}}\ \ (45)$

Relative the inertial coordinate system

${\hat {x}}\ ,\ {\hat {y}}$

in the orbital plane with ${\hat {x}}$ towards pericentre one gets from (18) and (19) that the velocity components are

$V_{x}=\cos \theta \cdot V_{r}-\sin \theta \cdot V_{t}=-{\sqrt {\frac {\mu }{p}}}\cdot \sin \theta \ \ (44)$

$V_{y}=\sin \theta \cdot V_{r}+\cos \theta \cdot V_{t}={\sqrt {\frac {\mu }{p}}}\cdot (e+\cos \theta )\ \ (45)$

Determination of the Kepler orbit that corresponds to a given initial state

This is the "initial value problem" for the differential equation (1) which is a first order equation for the 6-dimensional "state vector" $(\ {\bar {r}}\ ,{\bar {v}}\ )$ when written as

${\dot {\bar {v}}}=-\mu \cdot {\frac {\hat {r}}{r^{2}}}\ \ (46)$

${\dot {\bar {r}}}={\bar {v}}\ \ (47)$

For any values for the initial "state vector" $(\ {\bar {r_{0}}}\ ,{\bar {v_{0}}}\ )$ the Kepler orbit corresponding to the solution of this initial value problem can be found with the following algorithm:

Define the orthogonal unit vectors $({\hat {r}}\ ,\ {\hat {t}})$ through

${\bar {r_{0}}}=r\cdot {\hat {r}}\ \ (48)$

${\bar {v_{0}}}=V_{r}\cdot {\hat {r}}+V_{t}\cdot {\hat {t}}\ \ (49)$

with $r>0$ and $V_{t}>0$

From (13), (18) and (19) follows that by setting

$p={\frac {{(r\cdot V_{t})}^{2}}{\mu }}\ \ (50)$

and by defining $e\geq 0$ and $\theta$ such that

$e\cdot \cos \theta ={\frac {V_{t}}{V_{0}}}-1\ \ (51)$

$e\cdot \sin \theta ={\frac {V_{r}}{V_{0}}}\ \ (52)$

where

$V_{0}={\sqrt {\frac {\mu }{p}}}\ \ (53)$

one gets a Kepler orbit that for true anomaly $\theta$ has the same r, $V_{r}$ and $V_{t}$ values as those defined by (48) and (49).

If this Kepler orbit then also has the same $({\hat {r}}\ ,\ {\hat {t}})$ vectors for this true anomaly $\theta$ as the ones defined by (48) and (49) the state vector $({\bar {r}}\ ,\ {\bar {v}})$ of the Kepler orbit takes the desired values $(\ {\bar {r_{0}}}\ ,{\bar {v_{0}}}\ )$ for true anomaly $\theta$.

The standard inertially fixed coordinate system $({\hat {x}}\ ,\ {\hat {y}})$ in the orbital plane (with ${\hat {x}}$ directed from the centre of the homogeneous sphere to the pericentre) defining the orientation of the conical section (ellipse, parabola or hyperbola) can then be determined with the relation

${\hat {x}}=\cos \theta \cdot {\hat {r}}-\sin \theta \cdot {\hat {t}}\ \ (54)$

${\hat {y}}=\sin \theta \cdot {\hat {r}}+\cos \theta \cdot {\hat {t}}\ \ (55)$

Note that the relations (51) and (52) has a singularity when $V_{r}=0$ and

$V_{t}=V_{0}={\sqrt {\frac {\mu }{p}}}={\sqrt {\frac {\mu }{\frac {{(r\cdot V_{t})}^{2}}{\mu }}}}$

i.e.

$V_{t}={\sqrt {\frac {\mu }{r}}}\ \ (56)$

which is the case that it is a circular orbit that is fitting the initial state $(\ {\bar {r_{0}}}\ ,{\bar {v_{0}}}\ )$

The osculating Kepler orbit

Main article: Osculating orbit

For any state vector $(\ {\bar {r}}\ ,\ {\bar {v}}\ )$ the Kepler orbit corresponding to this state can be computed with the algorithm defined above. First the parameters $p\ ,\ e\ ,\ \theta$ are determined from $r\ ,\ V_{r}\ ,\ V_{t}$ and then the orthogonal unit vectors in the orbital plane ${\hat {x}}\ ,\ {\hat {y}}$ using the relations (54) and (55).

If now the equation of motion is

${\ddot {\bar {r}}}=\operatorname {\bar {F}} ({\bar {r}},{\dot {\bar {r}}},t)\ \ (57)$

where

$\operatorname {\bar {F}} ({\bar {r}},{\dot {\bar {r}}},t)$

is another function then

$-\mu \cdot {\frac {\hat {r}}{r^{2}}}$

the resulting parameters

$p\ ,\ e\ ,\ \theta ,\ {\hat {x}}\ ,\ {\hat {y}}$

defined by ${\bar {r}},{\dot {\bar {r}}}$ will all vary with time as opposed to the case of a Kepler orbit for which only the parameter $\theta$ will vary

The Kepler orbit computed in this way having the same "state vector" as the solution to the "equation of motion" (57) at time t is said to be "osculating" at this time.

This concept is for example useful in case

$\operatorname {\bar {F}} ({\bar {r}},{\dot {\bar {r}}},t)=-\mu \cdot {\frac {\hat {r}}{r^{2}}}+\operatorname {\bar {f}} ({\bar {r}},{\dot {\bar {r}}},t)$

where

$\operatorname {\bar {f}} ({\bar {r}},{\dot {\bar {r}}},t)$

is a small "perturbing force" due to for example a faint gravitational pull from other celestial bodies. The parameters of the osculating Kepler orbit will then only slowly change and the osculating Kepler orbit is a good approximation to the real orbit for a considerable time period before and after the time of osculation.

This concept can also be useful for a rocket during powered flight as it then tells which Kepler orbit the rocket would continue in in case the thrust is switched-off.

For a "close to circular" orbit the concept "eccentricity vector" defined as ${\bar {e}}=e\cdot {\hat {x}}$ is useful. From (51), (52) and (54) follows that

${\bar {e}}={\frac {(V_{t}-V_{0})\cdot {\hat {r}}-V_{r}\cdot {\hat {t}}}{V_{0}}}\ \ (58)$

i.e. ${\bar {e}}$ is a smooth differentiable function of the state vector $(\ {\bar {r}}\ ,{\bar {v}}\ )$ also if this state corresponds to a circular orbit.

Orbital elements

Keplerian orbital elements.

Main article: Orbital elements

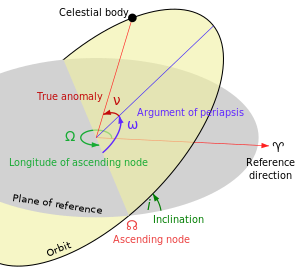
A Kepler orbit is specified by six orbital elements, normally the following (assuming an elliptical orbit; parabolas and hyperbolas are also possible if eccentricity >= 1).

Two define the shape and size of the ellipse:

• Eccentricity ($e\,\!$)
• Semimajor axis ($a\,\!$)

Two define the orientation of the orbital plane:

• Inclination ($i\,\!$)
• Longitude of the ascending node ($\Omega \,\!$)

And finally:

• Argument of periapsis ($\omega \,\!$) defines the orientation of the ellipse in the orbital plane.
• Mean anomaly at epoch ($M_{o}\,\!$) defines the position of the orbiting body along the ellipse. (True anomaly ($\nu \,\!$) is shown on the diagram, since mean anomaly does not represent a real geometric angle.)

External links

• JAVA applet animating the orbit of a satellite in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.