User:Earlster/Sandbox

Earlster/Sandbox

Example of insertion sort sorting a list of random numbers. Example of insertion sort sorting a list of random numbers.
Class	Sorting algorithm
Data structure	Array
Worst-case performance	$O(n)$
Best-case performance	$O(1)$
Average performance	$O(1.5)$
Worst-case space complexity	$O(n)$ total, $O(1)$

Elements are distributed among bins

Unlike bucket sorting which sorts after all the buckets are filled, the elements are insertion sorted as they are inserted

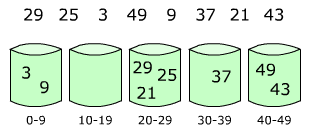
Proxmap Sorting, or just Proxmap, is a sort and searching algorithm that works by partitioning an array of data items, or keys, into a number of buckets. The name is short for computing a "proximity map," which indicates for each key K, the beginning of a subarray in the array A where K will reside in the final sorted order. If keys are "well distributed" amongst the buckets, sorting occurs in $O(n)$ time, much faster than comparison-based sorting, which can do no better than $O(nlogn)$. During generation a proxmap is created, which is used to find keys in an average of $O(1.5)$ time. It is a form of bucket and radix sort. The algorithm also scales up well with large data.

Keys are dropped into each bucket using insertion sort. Since bucket sort is not a comparison sort, the Ω(n log n) lower bound is inapplicable. The computational complexity estimates involve the number of buckets and the key used.

History

• Invented late 1980's by Thomas A. Standish, Prof. Emeritus, Bren School of ICS

Overview

Basic Strategy

Given an array A1:

• map a key to a subarray of the destination array A2, by applying a "mapkey" function to each array item
• determine how many keys will map to the same subarray or "bucket," using an array of "hit counts," H
• determine where each subarray will begin in the destination array so that each bucket is exactly the right size to hold all the keys that will map to it, an array of "proxmaps," P
• for each key, compute the bucket it will map to, an array of "locations," L
• for each key, look up it's location, place it into that cell of A2, if it keys with a key already in that position, insertion sort the key while maintaining the order of keys. Moving keys > this key to the right by one will free up a space for this key. Since the subarray is big enough to hold all the keys mapped to it, such movement will never cause the keys to overflow into the following subarray.

Simplied: Given an array unsortedList with n keys

1. Initialize: Create and initialize 4 arrays all of n size, hitCount, proxMap, location, and sortedList.
2. Partition: Using a carefully chosen mapKey function, divide the sortedList into subarrays or "buckets" using the keys in unsortedList
3. Disperse: Read over the unsortedList, dropping each key into its bucket in sortedList, insertion sorting as needed.
4. Collect: Visit the buckets in order and put all the elements back into the original array.

Example with Pseudocode

Consider a full array: A[0 to n-1] with n keys. Let i be an index of A. Sort A's keys into array A2 of equal size.

The MapKey(key) function will be defined as mapKey(int k) = floor(K).

Array table

A1	6.7	5.9	8.4	1.2	7.3	3.7	11.5	1.1	4.8	0.4	10.5	6.1	1.8
H	1	3	0	1	1	1	2	1	1	0	1	1
P	0	1	-1	4	5	6	7	9	10	-1	11	12
L	7	6	10	1	9	4	12	1	5	0	11	7	1
A2	0.4	1.1	1.2	1.8	3.7	4.8	5.9	6.1	6.7	7.3	8.4	10.5	11.1

Multiplication table

×	1	2	3
1	1	2	3
2	2	4	6
3	3	6	9
4	4	8	12
5	5	10	15

Pseudocode

for i = 0 to 11 // compute hit counts
H[i] = 0;
for i = 0 to 12
{
pos = MapKey(A[i]);
H[pos] = H[pos] + 1;
}

runningTotal = 0; // compute prox map – location of start of each subarray
for i = 0 to 12
if H[i] = 0
P[i] = 0;
else
P[i] = runningTotal;
runningTotal = runningTotal + H[i];

for i = 0 to 12 // compute location – subarray – in A2 into which each item in A is to be placed
L[i] = P[MapKey(A[i])];

for I = 0 to 12; // sort items
A2[I] = <empty>;
for i = 0 to 12 // insert each item into subarray beginning at start, preserving order
{
start = L[i]; // subarray for this item begins at this location
insertion made = false;
for j = start to an empty cell or the end of A2 is found, and insertion not made
{
if A2[j] == <empty> // if subarray empty, just put item in first position of subarray
A2[j] = A[i];
insertion made = true;
else if key < A2[j] // key belongs at A2[j]
int end = j + 1; // Find end of used part of bucket – where first <empty> is
while (A2[end] != <empty>
end++;
for k = end -1 to j // Move larger keys to the right 1 cell
A2[k+1] = A2[k];
A2[j] = A[i];
insertion made = true; // Add in new key
}
}

function proxmap-sort(array, mapKey) is
  hitCount ← new array of size n
  location ← new array of size n
  proxmap ← new array of size n
  sortedArray ← sorted array of size n
  for i = 0 to (length(array)-1) do
    insert array[i] into buckets[keyFunction(array[i], k)]
  for i = 0 to n - 1 do
    next-sort(buckets[i])
  return the concatenation of buckets[0], ..., buckets[n-1]

Here array is the array to be sorted and n is the number of buckets to use. The key function such as keyFunction(x,k) returns the k most significant bits of x (floor(x/2^(size(x)-k))); different functions can be used to translate the range of elements in array to n buckets, such as translating the letters A–Z to 0–25 or returning the first character (0–255) for sorting strings. Another method could simply take the floor of the incoming data divided by 10, or floor(k/10) Buckets get sorted as the data comes in, not all at the end.

Analysis

Computing H, P, and L all take $O(n)$ time. Each is computed with one pass through an array, with constant time spent at each array location.

• worst case:

MapKey places all items into 1 subarray so you get standard insertion sort, and time of $O(n^{2})$.

• best case:

MapKey delivers the same small number of items to each part of the array in an order where the best case of insertion sort occurs. Each insertion sort is $O(c)$, c the size of the parts; there are p parts thus p * c = n, so insertion sorts take O(n); thus, building proxMap is $O(n)$.

• average case:

Say size of each subarray is at most c, a constant; insertion sort is then O(c^2) at worst – a constant! (actually much better, since we don’t sort c items until the last item is placed in the bucket) total time is number of buckets, (n/c) , times $O(c^{2})$ = roughly n/c * c^2= n * c so time is $O(n)$.

• Having a good MapKey function is imperative for avoiding the worst case. We must know something about the distribution of the data to come up with a good key
• Save time: save MapKey(i) values so don’t have to re-compute them (notice they're recomputed in code above)
• Save space: if clever, can reuse array

Optimizations

Many optimizations include using the same array to store the sorted data, reusing the hitCount, proxMap, and location arrays used to sort the data. To be expanded on later...

Generic bucket sort related to Proxmap

The most common variant of bucket sort operates on a list of n numeric inputs between zero and some maximum value M and divides the value range into n buckets each of size M/n. If each bucket is sorted using insertion sort, the sort can be shown to run in expected linear time (where the average is taken over all possible inputs). However, the performance of this sort degrades with clustering; if many values occur close together, they will all fall into a single bucket and be sorted slowly. This holds a similar story with Proxmap, if the buckets are too large or too small then the performance of the function degrades severely.

Comparison with other sorting algorithms

Generally, it works relatively fast when compared with other sorting algorithms as its not comparison-based. The function is nearly constant access time which makes it very appealing for large databases. Despite the O(n) build time, it makes up for it with its O(1.5) average access time. If the array doesn't need to be updated often, the access time makes this function more favorable.

Proxmap Searching

Typically, Proxmap Sort is used along with Proxmap Searching, which uses the proxMap array generated by Proxmap Sort algorithm to find keys in the sorted array, or A2 in constant time.

Basic Strategy

• Build the proxmap structure, keeping MapKey routine, P and A2
• To search for a key, go to P[MapKey(k)], the start of the subarray that contains the key, if it is in the data set
• Sequential search the subarray; if find key, return it (and associated information) if find a value > key, key is not in the data set
• Computing P[MapKey(k)] takes O(1). If a mapkey that gives a good distribution of keys was used, each subarray is bounded above by a constant c, so at most c comparisons are needed to find key or know it is not present; therefore ProxmapSearch is O(1), once proxmap has been built. If the worst mapkey was used, all keys are in the same subarray, so ProxmapSearch, in this worst case, will require O(n) comparisons, once proxmap has been built.

Pseudocode

function mapKey(key)
  return floor(key)

  proxMap ← previously generated proxmap array of size n
  sortedArray ← previously sorted array of size n
function proxmap-search(key) is
  for i = proxMap[mapKey(key)] to (length(array)-1 do
    if (sortedArray[i] == key)
      return sortedArray[i].value

References

• Thomas A. Standish "Using O(n) ProxmapSort and O(1) ProxmapSearch to Motivate CS2 Students (Part I)" from Donald Bren School of Information and Computer Sciences at UC Irvine.
• Norman Jacobson "A Synopsis of ProxmapSort & ProxmapSearch" from Donald Bren School of Information and Computer Sciences at UC Irvine.

External links

• http://www.cs.uah.edu/~rcoleman/CS221/Sorting/ProxMapSort.html