Genetic programming: Difference between revisions
| Line 1,094: | Line 1,094: | ||
| Termination || A program with total error less than 0.1 is found |
| Termination || A program with total error less than 0.1 is found |
||
|} |
|} |
||
==== Initialisation ==== |
|||
GP starts by randomly creating a population of four individual computer programs. The four programs are shown in Figure [http://dces.essex.ac.uk/staff/rpoli/gp-field-guide/42StepbyStepSampleRun.html#x1-288r1|4.1] <!--\ref{fig:exampleInitialPop}!--> |
|||
in the form of trees. |
|||
The first randomly constructed program tree |
|||
<!--(Figure~\ref{fig:exampleInitialPop}a)!--> |
|||
is equivalent to the expression x+1. |
|||
The second program <!--(Figure~\ref{fig:exampleInitialPop}b)!--> |
|||
adds the |
|||
constant terminal 1 to the result of multiplying x by |
|||
x and is equivalent to x*x+1. The third program |
|||
<!--(Figure~\ref{fig:exampleInitialPop}c)!--> |
|||
adds the constant terminal 2 to |
|||
the constant terminal 0 and is equivalent to the constant |
|||
value 2. The fourth program <!--(Figure~\ref{fig:exampleInitialPop}d)!--> |
|||
is equivalent to x. |
|||
== History == |
== History == |
||
Revision as of 15:52, 6 May 2011
In artificial intelligence, genetic programming (GP) is an evolutionary algorithm-based methodology inspired by biological evolution to find computer programs that perform a user-defined task. It is a specialization of genetic algorithms (GA) where each individual is a computer program. It is a machine learning technique used to optimize a population of computer programs according to a fitness landscape determined by a program's ability to perform a given computational task.
Introduction
The goal of having computers automatically solve problems is central to artificial intelligence (AI) machine learning (ML), and the broad area encompassed by what Turing called "machine intelligence" (Turing, 1948)[1]. Machine learning pioneer Arthur Samuel, in his 1983 talk entitled "AI: Where It Has Been and Where It Is Going" (Samuel, 1983)[2], stated that the main goal of the fields of machine learning and artificial intelligence is:
to get machines to exhibit behaviour, which if done by humans, would be assumed to involve the use of intelligence.
Genetic programming (GP) is an evolutionary computation (EC) technique that automatically solves problems without requiring the user to know or specify the form or structure of the solution in advance. At the most abstract level GP is a systematic, domain-independent method for getting computers to solve problems automatically starting from a high-level statement of what needs to be done.
Since its inception, GP has attracted the interest of myriads of people around the globe.
Genetic Programming in a Nutshell
In genetic programming we evolve a population of computer programs. That is, generation by generation, GP stochastically transforms populations of programs into new, hopefully better, populations of programs, cf. Figure [1]. GP, like nature, is a random process, and it can never guarantee results. GP's essential randomness, however, can lead it to escape traps which deterministic methods may be captured by. Like nature, GP has been very successful at evolving novel and unexpected ways of solving problems. (See (Poli, 2008, Chapter 12)[3] [http://cswww.essex.ac.uk/staff/rpoli/gp-field-guide/121WhereGPhasDoneWelll23.html for numerous examples].)
The basic steps in a GP system are shown in Algorithm 1.1.
GP finds out how well a program works by running it, and then comparing its
behaviour to some ideal (line 3).
We might be interested, for example, in
how well a program predicts a time series or controls an industrial process.
This comparison is quantified to give a numeric value called
fitness.
Those programs that do well are chosen to breed (line 4)
and produce new
programs for the next generation (line 5).
The primary genetic operators
that are used to create new programs from existing ones are:
- Crossover: The creation of a child program by combining randomly chosen parts from two selected parent programs.
- Mutation: The modification of a child program by altering a randomly chosen part of it.
| Algorithm 1.1: Genetic Programming |
|---|
|
Getting Started
Two key questions for those first exploring GP are:
- What should I read to get started in GP?
- Should I implement my own GP system or should I use an existing package? If so, what package should I use?
There are many books on GP, including Koza's four massive contributions. The Field Guide to Genetic Programming[4] is more recent and available online. No single article could claim to be completely comprehensive. The sections at the end of this article (esp. Bibliography) list many sources. There are also a whole host of books, videos, journals, conferences, and on-line sources (including several freely available GP systems) that should be of assistance.
We strongly encourage doing GP as well as reading about it; the dynamics of evolutionary algorithms are complex, and the experience of tracing through runs is invaluable. Section Implementations lists many free GP systems. Typically they are distributed as source code.
Representation, Initialisation and Operators in Tree-based GP
Representation
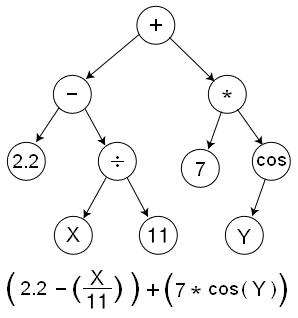
In GP, programs are usually expressed as syntax tree rather than as lines of code. The figure shows the tree representation of the program 2.2 -x/11 + 7*cos(y). The variables and constants in the program (x, y and 2.2, 11 and 7) are leaves of the tree. In GP they are called terminals, whilst the arithmetic operations (+, - * and /) are internal nodes called functions. The sets of allowed functions and terminals together form the primitive set of a GP system.
In more advanced forms of GP, programs can be composed of multiple components (e.g., subroutines). In this case the representation used in GP is a set of trees (one for each component) grouped together under a special root node that acts as glue, as illustrated in Figure [2]. We will call these (sub)trees branches. The number and type of the branches in a program, together with certain other features of their structure, form the architecture of the program.
It is common in the GP literature to represent expressions in a
prefix notation similar to that used in Lisp or Scheme. For
example,
2.2 -x/11 + 7*cos(y) becomes (+ (- 2.2 (/ x 11) (* 7 (cos y)))).
This notation often makes it easier to see the relationship between (sub)expressions and their corresponding (sub)trees. Therefore we will use trees and their corresponding prefix-notation expressions interchangeably.
How one implements tree-based representation GP trees will obviously depend a great deal on the programming languages and libraries being used. Languages that provide automatic garbage collection and dynamic lists as fundamental data types make it easier to implement expression trees and the necessary GP operations. Most traditional languages used in AI research (e.g., Lisp and Prolog), many recent languages (e.g., Ruby and Python), and the languages associated with several scientific programming tools (e.g., MATLAB and Mathematica) have these facilities. In other languages, one may have to implement lists/trees or use libraries that provide such data structures.
In high performance environments, the tree-based representation of programs may be too inefficient since it requires the storage and management of numerous pointers. In some cases, it may be desirable to use GP primitives which accept a variable number of arguments (a quantity we will call arity). An example is the sequencing instruction progn, which accepts any number of arguments, executes them one at a time and then returns the value returned by the last argument. However, fortunately, it is now extremely common in GP applications for all functions to have a fixed number of arguments. If this is the case, then, the brackets in prefix-notation expressions are redundant, and trees can efficiently be represented as simple linear sequences. In effect, the function's name gives its arity and from the arities the brackets can be inferred. For example, the expression (+ (- 2.2 (/ x 11) (* 7 (cos y)))) could be written unambiguously as the sequence + - 2.2 / x 11 * 7 cos y.
The choice of whether to use such a linear representation or an explicit tree representation is typically guided by questions of convenience, efficiency, the genetic operations being used (some may be more easily or more efficiently implemented in one representation), and other data one may wish to collect during runs. (It is sometimes useful to attach additional information to nodes, which may be easier to implement if they are explicitly represented).
These tree representations are the most common in GP, e.g., numerous high-quality, freely available GP implementations use them (see implementations). However, there are other important representations, e.g. linear and graph based GP.
Initialising the Population
Like in other evolutionary algorithms, in GP the individuals in the initial population are typically randomly generated. There are a number of different approaches to generating this random initial population. Here we will describe two of the simplest (and earliest) methods (the full and grow methods), and a widely used combination of the two known as Ramped half-and-half.
In both the full and grow methods, the initial individuals are generated so that they do not exceed a user specified maximum depth. The depth of a node is the number of edges that need to be traversed to reach the node starting from the tree's root node (which is assumed to be at depth 0). The depth of a tree is the depth of its deepest leaf (e.g., the tree in first figure has a depth of 3). In the full method (so named because it generates full trees, i.e. all leaves are at the same depth) nodes are taken at random from the function set until the maximum tree depth is reached. (Beyond that depth, only terminals can be chosen.) Figure [3] shows a series of snapshots of the construction of a full tree of depth 2. The children of the * and / nodes must be leaves or otherwise the tree would be too deep. Thus, at both steps t=3, t=4, t=6 and t=7 a terminal must be chosen. (x, y, 1 and 0 were chosen).
Although, the full method generates trees where all the leaves are at the same
depth, this does not necessarily mean that all initial trees will have
an identical number of nodes (often referred to as the size of a
tree)
or the same
shape. This only happens, in fact, when all the functions in the
primitive set have an equal arity.
Nonetheless, even when mixed-arity primitive sets are used, the range
of program sizes and shapes produced by the full method may be rather
limited.
The grow method, on the contrary, allows for the
creation of trees of more varied sizes and shapes. Nodes are selected from
the whole primitive set (i.e., functions and terminals) until the
depth limit is reached. Once the depth limit is reached only
terminals may be chosen (just as in the full method).
Figure [4]
illustrates this process for the construction of
a tree with depth limit 2. Here the first argument of the + root
node happens to be a terminal. This closes off that branch
preventing it from growing any more before it reached the depth limit.
The other argument is a function (-), but its arguments are
forced to be terminals to ensure that the resulting tree does not
exceed the depth limit.
Pseudocode for a recursive implementation of both the full and grow methods is given in Algorithm 2.1.
- if max_d = 0 or (method = grow and random then
- expr = choose_random_element( term_set )
- else
- func = choose_random_element( func_set )
- for i = 1 to arity(func)
- arg_i = gen_rnd_expr( func_set, term_set, max_d - 1, method )
- endfor
- expr = (func, arg_1, arg_2, ...)
- endif
- return expr
| Algorithm 2.1: Pseudocode for recursive program generation with the full and grow methods. |
|---|
Because neither the grow or full method provide a very wide array of sizes or shapes on their own, Koza[5] proposed a combination called ramped half-and-half. Half the initial population is constructed using full and half is constructed using grow. This is done using a range of depth limits (hence the term ramped) to help ensure that we generate trees having a variety of sizes and shapes.
While these methods are easy to implement and use, they often make it difficult to control the statistical distributions of important properties such as the sizes and shapes of the generated trees. For example, the sizes and shapes of the trees generated via the grow method are highly sensitive to the sizes of the function and terminal sets. If, for example, one has significantly more terminals than functions, the grow method will almost always generate very short trees regardless of the depth limit. Similarly, if the number of functions is considerably greater than the number of terminals, then the grow method will behave quite similarly to the full method. The arities of the functions in the primitive set also influence the size and shape of the trees produced by grow. Page 50 of the Field Guide describes other initialisation mechanisms which address these issues.
The initial population need not be entirely random. If something is known about likely properties of the desired solution, trees having these properties can be used to seed the initial population.
Selection
As with most evolutionary algorithms, genetic operators in GP are applied to individuals that are probabilistically selected based on fitness. That is, better individuals are more likely to have more child programs than inferior individuals. The most commonly employed method for selecting individuals in GP is tournament selection, which is discussed below, followed by fitness-proportionate selection, but any standard evolutionary algorithm selection mechanism can be used.
In tournament selection a number of individuals are chosen at random from the population. These are compared with each other and the best of them is chosen to be the parent. When doing crossover, two parents are needed and, so, two selection tournaments are made. Note that tournament selection only looks at which program is better than another. It does not need to know how much better. This effectively automatically rescales fitness, so that the selection pressure on the population remains constant. Thus, a single extraordinarily good program cannot immediately swamp the next generation with its children; if it did, this would lead to a rapid loss of diversity with potentially disastrous consequences for a run. Conversely, tournament selection amplifies small differences in fitness to prefer the better program even if it is only marginally superior to the other individuals in a tournament.
An element of noise is inherent in tournament selection due to the random selection of candidates for tournaments. So, while preferring the best, tournament selection does ensure that even average-quality programs have some chance of having children. Since tournament selection is easy to implement and provides automatic fitness rescaling, it is commonly used in GP.
Considering that selection has been described many times in the evolutionary algorithms literature, we will not provide details of the numerous other mechanisms that have been proposed. (Goldberg, 1989)[6], for example, describes fitness-proportionate selection, stochastic universal sampling and several others.
Recombination and Mutation
GP departs significantly from other evolutionary algorithms in the implementation of the operators of crossover and mutation. The most commonly used form of crossover is subtree crossover. Given two parents, subtree crossover randomly (and independently) selects a crossover point (a node) in each parent tree. Then, it creates the offspring by replacing the subtree rooted at the crossover point in a copy of the first parent with a copy of the subtree rooted at the crossover point in the second parent, as illustrated in Figure [5]. Copies are used to avoid disrupting the original individuals. This way, if selected multiple times, they can take part in the creation of multiple offspring programs. Note that it is also possible to define a version of crossover that returns two offspring, but this is not commonly used.
Often crossover points
are not selected with uniform probability. Typical GP primitive
sets lead to trees with an average branching factor (the number of children of each node)
of at least two, so the majority of the nodes will be leaves. Consequently the
uniform selection of crossover points leads to crossover
operations frequently exchanging only very small amounts of genetic material (i.e., small
subtrees); many crossovers may in fact reduce to simply swapping two
leaves. To counter this, Koza[7]
suggested the widely used approach of choosing
functions 90% of the time and leaves 10% of the time.
Many other types of crossover and mutation of GP trees are possible.
The most commonly used form of mutation in GP (which we will call
subtree mutation) randomly selects a mutation point in a tree and
substitutes the subtree rooted there with a randomly generated
subtree. This is illustrated in Figure [6].
Subtree mutation is sometimes implemented as crossover between a
program and a newly generated random program; this operation is also
known as
headless chicken crossover[8].
Another common form of mutation is point mutation, which is GP's rough equivalent of the bit-flip mutation used in genetic algorithms[9]. In point mutation, a random node is selected and the primitive stored there is replaced with a different random primitive of the same arity taken from the primitive set. If no other primitives with that arity exist, nothing happens to that node (but other nodes may still be mutated). When subtree mutation is applied, this involves the modification of exactly one subtree. Point mutation, on the other hand, is typically applied on a per-node basis. That is, each node is considered in turn and, with a certain probability, it is altered as explained above. This allows multiple nodes to be mutated independently in one application of point mutation.
The choice of which of the operators described above should be used to create an offspring is probabilistic. Operators in GP are normally mutually exclusive (unlike other evolutionary algorithms where offspring are sometimes obtained via a composition of operators). Their probability of application are called operator rates. Typically, crossover is applied with the highest probability, the crossover rate often being 90 percent or higher. On the contrary, the mutation rate is much smaller, typically being in the region of one percent.
When the rates of crossover and mutation add up to a value p which is less than 100%, an operator called reproduction is also used, with a rate of 1-p. Reproduction simply involves the selection of an individual based on fitness and the insertion of a copy of it in the next generation.
Getting Ready to Run Genetic Programming
To apply a GP system to a problem, several decisions need to be made; these are often termed the preparatory steps. The key choices are:
- What is the terminal set?
- What is the function set?
- What is the fitness measure?
- What parameters will be used for controlling the run?
- What will be the termination criterion, and what will be designated the result of the run?
Terminal Set
While it is common to describe GP as evolving programs, GP is not typically used to evolve programs in the familiar Turing-complete languages humans normally use for software development. It is instead more common to evolve programs (or expressions or formulae) in a more constrained and often domain-specific language. The first two preparatory steps, the definition of the terminal and function sets, specify such a language. That is, together they define the ingredients that are available to GP to create computer programs.
The terminal set may consist of:
- the program's external inputs. These typically take the form of named variables (e.g., x, y).
- functions with no arguments. These may be included because they return different values each time they are used, such as the function rand() which returns random numbers, or a function dist_to_wall() that returns the distance to an obstacle from a robot that GP is controlling. Another possible reason is because the function produces side effects. Functions with side effects do more than just return a value: they may change some global data structures, print or draw something on the screen, control the motors of a robot.
- constants. These can be pre-specified, randomly generated as part of the tree creation process, or created by mutation.
Using a primitive such as rand can cause the behaviour of an individual program to vary every time it is called, even if it is given the same inputs. This is desirable in some applications. However, we more often want a set of fixed random constants that are generated as part of the process of initialising the population. This is typically accomplished by introducing a terminal that represents an ephemeral random constant. Every time this terminal is chosen in the construction of an initial tree (or a new subtree to use in an operation like mutation), a different random value is generated which is then used for that particular terminal, and which will remain fixed for the rest of the run. The use of ephemeral random constants is typically denoted by including the symbol R in the terminal set;
Function Set
The function set used in GP is typically driven by the nature of the problem domain. In a simple numeric problem, for example, the function set may consist of merely the arithmetic functions (+, -, *, /). However, all sorts of other functions and constructs typically encountered in computer programs can be used. Sometimes the primitive set includes specialised functions and terminals which are designed to solve problems in a specific problem domain. For example, if the goal is to program a robot to mop the floor, then the function set might include such actions as move, turn, and swish-the-mop.
Closure
For GP to work effectively, most function sets are required to have an important property known as closure, which can in turn be broken down into the properties of type consistency and evaluation safety.
Type consistency is required because subtree crossover can mix and join nodes arbitrarily. As a result it is necessary that any subtree can be used in any of the argument positions for every function in the function set, because it is always possible that subtree crossover will generate that combination. It is thus common to require that all the functions be type consistent, i.e., they all return values of the same type, and that each of their arguments also have this type. For example +, -, *, and / can can be defined so that they each take two integer arguments and return an integer. Sometimes type consistency can be weakened somewhat by providing an automatic conversion mechanism between types. We can, for example, convert numbers to Booleans by treating all negative values as false, and non-negative values as true. However, conversion mechanisms can introduce unexpected biases into the search process, so they should be used with care.
The type consistency requirement can seem quite limiting but often simple restructuring of the functions can resolve apparent problems. For example, an if function is often defined as taking three arguments: the test, the value to return if the test evaluates to true and the value to return if the test evaluates to false. The first of these three arguments is clearly Boolean, which would suggest that if can't be used with numeric functions like +. This, however, can easily be worked around by providing a mechanism to convert a numeric value into a Boolean automatically as discussed above. Alternatively, one can replace the 3-input if with a function of four (numeric) arguments a, b, c, d. The 4-input if implements "If a<b then return value c otherwise return value d".
An alternative to requiring type consistency is to extend the GP system. Crossover and mutation might explicitly make use of type information so that the children they produce do not contain illegal type mismatches. When mutating a legal program, for example, mutation might be required to generate a subtree which returns the same type as the subtree it has just deleted.
The other component of closure is evaluation safety. Evaluation safety is required because many commonly used functions can fail at run time. An evolved expression might, for example, divide by zero, or call MOVE_FORWARD when facing a wall or precipice. This is typically dealt with by modifying the normal behaviour of primitives. It is common to use protected versions of numeric functions that can otherwise throw exceptions, such as division, logarithm, exponential and square root. The protected version of a function first tests for potential problems with its input(s) before executing the corresponding instruction; if a problem is spotted then some default value is returned. Protected division (often notated with %) checks to see if its second argument is 0. If so, % typically returns the value 1 (regardless of the value of the first argument). Similarly, in a robotic application a MOVE_AHEAD instruction can be modified to do nothing if a forward move is illegal or if moving the robot might damage it.
An alternative to protected functions is to trap run-time exceptions and strongly reduce the fitness of programs that generate such errors. However, if the likelihood of generating invalid expressions is very high, this can lead to too many individuals in the population having nearly the same (very poor) fitness. This makes it hard for selection to choose which individuals might make good parents.
One type of run-time error that is more difficult to check for is numeric overflow. If the underlying implementation system throws some sort of exception, then this can be handled either by protection or by penalising as discussed above. However, it is common for implementation languages to ignore integer overflow quietly and simply wrap around. If this is unacceptable, then the GP implementation must include appropriate checks to catch and handle such overflows.
Sufficiency
There is one more property that primitives sets should have: sufficiency. Sufficiency means it is possible to express a solution to the problem at hand using the elements of the primitive set. Unfortunately, sufficiency can be guaranteed only for those problems where theory, or experience with other methods, tells us that a solution can be obtained by combining the elements of the primitive set.
As an example of a sufficient primitive set consider {AND, OR, NOT, x1, x2, ..., xN}. It is always sufficient for Boolean induction problems, since it can produce all Boolean functions of the variables x1, x2, ..., xN. Where as {+, -, *, /, x, 0, 1, 2}, is insufficient, since it is not able to represent transcendental functions. The function exp(x), for example, is transcendental and therefore cannot be expressed as a rational function (basically, a ratio of polynomials), and so cannot be represented exactly by any combination of {+, -, *, /, x, 0, 1, 2}. When a primitive set is insufficient, GP can only develop programs that approximate the desired one. However, in many cases such an approximation can be very close and good enough for the user's purpose. Adding a few unnecessary primitives in an attempt to ensure sufficiency does not tend to slow down GP overmuch, although there are cases where it can bias the system in unexpected ways.
Evolving Structures other than Programs
There are many problems where solutions cannot be directly cast as computer programs. For example, in many design problems the solution is an artifact of some type: a bridge, a circuit, an antenna, a lens, etc. GP has been applied to problems of this kind by using a trick: the primitive set is set up so that the evolved programs construct solutions to the problem. This is analogous to the process by which an egg grows into a chicken. For example, if the goal is the automatic creation of an electronic controller for a plant, the function set might include common components such as integrator, differentiator, wire, time lag, and gain, and the terminal set might contain reference, signal, and plant output. Each of these primitives, when executed, inserts the corresponding device into the controller being built. If, on the other hand, the goal is to synthesise analogue electrical circuits, the function set might include components such as transistors, capacitors, resistors, etc.
Fitness Function
The first two preparatory steps define the primitive set for GP, and therefore indirectly define the search space GP will explore. This includes all the programs that can be constructed by composing the primitives in all possible ways. However, at this stage, we still do not know which elements or regions of this search space are good. I.e., which regions of the search space include programs that solve, or approximately solve, the problem. This is the task of the fitness measure, which is our primary (and often sole) mechanism for giving a high-level statement of the problem's requirements to the GP system. For example, suppose the goal is to get GP to synthesise an amplifier automatically. Then the fitness function is the mechanism which tells GP to synthesise a circuit that amplifies an incoming signal. (As opposed to evolving a circuit that suppresses the low frequencies of an incoming signal, or computes its square root, etc. etc.)
Fitness can be measured in many ways. For example, in terms of: the amount of error between its output and the desired output; the amount of time (fuel, money, etc.) required to bring a system to a desired target state; the accuracy of the program in recognising patterns or classifying objects; the payoff that a game-playing program produces; the compliance of a structure with user-specified design criteria.
There is something unusual about the fitness functions used in GP that differentiates them from those used in most other evolutionary algorithms. Because the structures being evolved in GP are computer programs, fitness evaluation normally requires executing all the programs in the population, typically multiple times. While one can compile the GP programs that make up the population, the overhead of building a compiler is usually substantial, so it is much more common to use an interpreter to evaluate the evolved programs.
Interpreting a program tree means executing the nodes in the tree in an order that guarantees that nodes are not executed before the value of their arguments (if any) is known. This is usually done by traversing the tree recursively starting from the root node, and postponing the evaluation of each node until the values of its children (arguments) are known. \index{side effects} Other orders, such as going from the leaves to the root, are possible. If none of the primitives have side effects, the two orders are equivalent. This depth-first recursive process is illustrated in Figure [7] Algorithm 3.1 gives a pseudocode implementation of the interpretation procedure. The code assumes that programs are represented as prefix-notation expressions and that such expressions can be treated as lists of components.
| procedure: eval( expr ) | ||||
|---|---|---|---|---|
| if expr is a list then | ||||
| proc = expr(1) | Non-terminal: extract root | |||
| if proc is a function then | ||||
| value = proc( eval(expr(2)), eval(expr(3)), ... ) | Function: evaluate arguments | |||
| else | ||||
| value = proc( expr(2), expr(3), ...) | Macro: don't evaluate arguments | |||
| end if | ||||
| else | ||||
| if expr is a variable or expr is a constant then | ||||
| value = expr | Terminal variable or constant: just read the value | |||
| else | ||||
| value = expr() | Terminal 0-arity function: execute | |||
| end if | ||||
| end if | ||||
| return value | ||||
| Notes: expr is an expression in prefix notation, expr(1) represents the primitive at the root of the expression, expr(2) represents the first argument of that primitive, expr(3) represents the second argument, etc. | ||||
| Algorithm 3.1 Interpreter for genetic programming | ||||
In some problems we are interested in the output produced by
a program, namely the value returned when we evaluate the tree starting at the
root node. In other problems we are interested in the
actions performed by a program composed of functions with side effects.
In either case the fitness of a program typically
depends on the results produced by its execution on many different
inputs or under a variety of different conditions.
For example the program might be tested on all possible combinations of
inputs x1, x2, ..., xN.
Alternatively, a robot control program might be tested
with the robot in a number of starting locations.
These different
test cases typically contribute to the fitness value of
a program incrementally, and for this reason are called
fitness cases.
Another common feature of GP fitness measures is that, for many practical problems, they are multi-objective, i.e., they combine two or more different elements that are often in competition with one another. The area of multi-objective optimisation is a complex and active area of research in GP and machine learning in general[10].
Genetic Programming Parameters
The fourth preparatory step specifies the control parameters for the run. The most important control parameter is the population size. Other control parameters include the probabilities of performing the genetic operations, the maximum size for programs and other details of the run.
It is impossible to make general recommendations for setting optimal
parameter values, as
these depend too much on the details of the application.
However, genetic programming is in practice robust,
and it is likely that many different parameter values will work.
As a consequence,
one need not typically spend a long time tuning GP
for it to work adequately.
Creating the initial GP Population
It is common to create the initial population randomly using ramped half-and-half with a depth range of 2-6. The initial tree sizes will depend upon the number of the functions, the number of terminals and the arities of the functions. However, evolution will quickly move the population away from its initial distribution.
Proportion of GP children created by crossover or mutation
Traditionally, 90 percent of children are created by subtree crossover. However, the use of a 50-50 mixture of crossover and a variety of mutations also appears to work well.
Number of GP children
In many cases, the main limitation on the population size is the time taken to evaluate the fitnesses, not the space required to store the individuals. As a rule one prefers to have the largest population size that your system can handle gracefully; normally, the population size should be at least 500, and people often use much larger populations. Often, to a first approximation, GP runtime can be estimated by the product of: the number of runs R, the number of generations G, the size of the population P, the average size of the programs $s$ and the number of fitness cases F.
Number of Generations, size/depth limits on GP children
Typically, the number of generations is limited to between ten and fifty; the most productive search is usually performed in those early generations, and if a solution hasn't been found then, it's unlikely to be found in a reasonable amount of time. The folk wisdom on population size is to make it as large as possible, but there are those who suggest using many runs with much smaller populations instead. Some implementations do not require arbitrary limits of tree size. Even so, because of bloat (the uncontrolled growth of program sizes during GP runs, it is common to impose either a size or a depth limit or both.
Number and use of Fitness Cases
Sometimes the number of fitness cases is limited by the amount of training data available. In this case, the fitness function should use all of it. (One does not necessarily need to use verification or holdout data, since over-fitting can be avoided by other means ) In other cases, e.g.\ 22-bit even parity, there can almost be too much training data. Then the fitness function may be reduced to use just a subset of the training data. This does not necessarily have to be done manually as there are a number of algorithms that dynamically change the test set as the GP runs.
It is common to record the GP parameters in a table.
Stopping the Run and Choosing a Solution
The fifth preparatory step consists of specifying the termination criterion and the method of designating the result of the run. The termination criterion may include a maximum number of generations to be run as well as a problem-specific success predicate, such as the error falls below one percent. Typically, the best-so-far program is then harvested and designated as the result of the run, although one might wish to return additional individuals and data as necessary or appropriate for the problem domain.
Example Genetic Programming Run
This is an illustrative run of GP in which the goal is to automatically create a program with a target input/output behaviour. In particular, we want to evolve an expression whose values match those of x*x+x+1 in the range [-1, +1]. The process of mechanically creating a computer program that fit certain numerical data is sometimes called system identification or symbolic regression.
We begin with the five preparatory steps from the previous section and then describe in detail the events in one run.
Preparatory Steps
The purpose of the first two preparatory steps is to specify the ingredients the evolutionary process can use to construct potential solutions. Because the problem is to find a mathematical function of one independent variable, x, the terminal set (the inputs of the to-be-evolved programs) must include this variable. The terminal set also includes ephemeral random constants drawn from some reasonable range. What is a ``reasonable range is likely to be extremely problem dependent. While in theory you can build up large constants using small constants and arithmetic operators, the performance of your system is likely to improve considerably if you provide constants of roughly the right magnitude from the beginning. Your choice of genetic operators can also be important here. If you're finding that your system is struggling to evolve the right constants, it may be helpful to introduce mutation operators specifically designed to search of the space of constants. In this example we chose constants candomly from -5.0 to +5.0, as described in Section 3.1. Thus the terminal set, T, is T = {x, Re}.
The statement of the problem does not specify which functions may be employed in the to-be-evolved program. One simple choice for the function set is the four ordinary arithmetic functions: addition, subtraction, multiplication and division. Most numeric regression problems will require at least these operations, sometimes with additional functions such as sin and log. We will use the simple function set F = {+, -, *, %}, where % is protected division as discussed in Section 3.2.1 The target polynomial can be expressed exactly using the terminal and function sets we have chosen, so these primitives are sufficient for the quadratic polynomial problem. (cf. Sufficiency above.)
The third preparatory step involves constructing the fitness measure that specifies what the user wants. The high-level goal of this problem is to find a program whose output is equal to the values of the quadratic polynomial x*x2+x+1. Therefore, the fitness assigned to a particular individual in the population must reflect how closely the output of an individual program comes to the target polynomial x*x + x + 1.
In principle, the fitness measure could be defined in terms of the mathematical integral of the difference between the evolved function and the target function. However, for most symbolic regression problems, it is not practical or even possible to compute the value of the integral analytically. Thus, it is common to define the fitness to be the sum of absolute errors measured at different values of the independent variable x in the range -1.0, +1.0. In particular, we will measure the errors for x {-1.0, -0.9, ... , 0.9, 1.0}. A smaller value of fitness (error) is better; a fitness (error) of zero would indicate a perfect fit. With this definition, our fitness is (approximately) proportional to the area between the parabola x*x+x+1 and the curve representing the candidate individual (see [http://dces.essex.ac.uk/staff/rpoli/gp-field-guide/42StepbyStepSampleRun.html#x1-289r2%7C Figure 4.2] for examples).
The fourth step is where we set our run parameters. The population size in this small illustrative example will be just four. The population size for a run of GP typically consists of thousands of individuals, but we will use this tiny population size to keep the example manageable. The crossover operation is commonly used to generate about 90% of the individuals in the population; the reproduction operation (where a fit individual is simply copied from one generation to the next) is used to generate about 8% of the population; the mutation operation is used to generate about 1% of the population; and the architecture-altering operations are used to generate perhaps 1% of the population. However, because this example involves an abnormally small population of only four individuals, the crossover operation will be used twice (each time generating one individual), which corresponds to a crossover rate of 50%, while the mutation and reproduction operations will each be used to generate one individual. These are therefore applied with a rate of 25% each. For simplicity, the architecture-altering operations are not used for this problem.
In the fifth and final step we need to specify a termination condition. A reasonable termination criterion for this problem is that the run will continue from generation to generation until the fitness (or error) of some individual is less than 0.1. In this contrived example, our example run will (atypically) yield an algebraically perfect solution with a fitness of zero after just one generation.
Step-by-Step Sample Run
Now that we have performed the five preparatory steps, the run of GP can be launched. The GP setup is summarised in the Table
| Parameters for example genetic programming run | |
|---|---|
| Objective | Find program whose output matches x*x+x+1 over the range -1 < x < +1. |
| Function set | +, -, % (protected division), and *; all operating on floats |
| Terminal set | x, and constants chosen randomly between -5 and +5 |
| Fitness | sum of absolute errors for x = {-1.0, -0.9, ... 0.9, 1.0} |
| Selection | fitness proportionate (roulette wheel) non elitist |
| Initial population | ramped half-and-half (depth 1 to 2. 50% of terminals are constants) |
| Parameters | population size 4, 50% subtree crossover, 25% reproduction, 25% subtree mutation, no tree size limits. |
| Termination | A program with total error less than 0.1 is found |
Initialisation
GP starts by randomly creating a population of four individual computer programs. The four programs are shown in Figure [8] in the form of trees.
The first randomly constructed program tree is equivalent to the expression x+1. The second program adds the constant terminal 1 to the result of multiplying x by x and is equivalent to x*x+1. The third program adds the constant terminal 2 to the constant terminal 0 and is equivalent to the constant value 2. The fourth program is equivalent to x.
History
In 1954, GP began with the evolutionary algorithms first used by Nils Aall Barricelli applied to evolutionary simulations. In the 1960s and early 1970s, evolutionary algorithms became widely recognized as optimization methods. Ingo Rechenberg and his group were able to solve complex engineering problems through evolution strategies as documented in his 1971 PhD thesis and the resulting 1973 book. John Holland was highly influential during the 1970s.
In 1964, Lawrence J. Fogel, one of the earliest practitioners of the GP methodology, applied evolutionary algorithms to the problem of discovering finite-state automata. Later GP-related work grew out of the learning classifier system community, which developed sets of sparse rules describing optimal policies for Markov decision processes. The first statement of modern "tree-based" Genetic Programming (that is, procedural languages organized in tree-based structures and operated on by suitably defined GA-operators) was given by Nichael L. Cramer (1985),.[11] This work was later greatly expanded by John R. Koza, a main proponent of GP who has pioneered the application of genetic programming in various complex optimization and search problems.[12]
In the 1990s, GP was mainly used to solve relatively simple problems because it is very computationally intensive. Recently GP has produced many novel and outstanding results in areas such as quantum computing, electronic design, game playing, sorting, and searching, due to improvements in GP technology and the exponential growth in CPU power.[13] These results include the replication or development of several post-year-2000 inventions. GP has also been applied to evolvable hardware as well as computer programs.
Developing a theory for GP has been very difficult and so in the 1990s GP was considered a sort of outcast among search techniques. But after a series of breakthroughs in the early 2000s, the theory of GP has had a formidable and rapid development. So much so that it has been possible to build exact probabilistic models of GP (schema theories and Markov chain models). [citation needed][dubious – discuss]
Chromosome representation
GP evolves computer programs, traditionally represented in memory as tree structures.[14] Trees can be easily evaluated in a recursive manner. Every tree node has an operator function and every terminal node has an operand, making mathematical expressions easy to evolve and evaluate. Thus traditionally GP favors the use of programming languages that naturally embody tree structures (for example, Lisp; other functional programming languages are also suitable).
Non-tree representations have been suggested and successfully implemented, such as linear genetic programming which suits the more traditional imperative languages [see, for example, Banzhaf et al. (1998)]. The commercial GP software Discipulus, uses AIM, automatic induction of binary machine code[15] to achieve better performance. µGP[16] uses a representation similar to linear GP to generate programs that fully exploit the syntax of a given assembly language.
Genetic operators
The main operators used in evolutionary algorithms such as GP are crossover and mutation.
Crossover
Crossover is applied on an individual by simply switching one of its nodes with another node from another individual in the population. With a tree-based representation, replacing a node means replacing the whole branch. This adds greater effectiveness to the crossover operator. The expressions resulting from crossover are very much different from their initial parents.
The following code suggests a simple implementation of individual deformation using crossover:
individual.Children[randomChildIndex] = otherIndividual.Children[randomChildIndex];
Mutation
Mutation affects an individual in the population. It can replace a whole node in the selected individual, or it can replace just the node's information. To maintain integrity, operations must be fail-safe or the type of information the node holds must be taken into account. For example, mutation must be aware of binary operation nodes, or the operator must be able to handle missing values.
A simple piece of code:
individual.Information = randomInformation();
or
individual = generateNewIndividual();
Meta-Genetic Programming
Meta-Genetic Programming is the proposed meta learning technique of evolving a genetic programming system using genetic programming itself. It suggests that chromosomes, crossover, and mutation were themselves evolved, therefore like their real life counterparts should be allowed to change on their own rather than being determined by a human programmer. Meta-GP was formally proposed by Jürgen Schmidhuber in 1987,[17] but some earlier efforts may be considered instances of the same technique, including Doug Lenat's Eurisko. It is a recursive but terminating algorithm, allowing it to avoid infinite recursion.
Critics of this idea often say this approach is overly broad in scope. However, it might be possible to constrain the fitness criterion onto a general class of results, and so obtain an evolved GP that would more efficiently produce results for sub-classes. This might take the form of a Meta evolved GP for producing human walking algorithms which is then used to evolve human running, jumping, etc. The fitness criterion applied to the Meta GP would simply be one of efficiency.
For general problem classes there may be no way to show that Meta GP will reliably produce results more efficiently than a created algorithm other than exhaustion. The same holds for standard GP and other search algorithms.
Implementations
Possibly most used:
- ECJ - Evolutionary Computation/Genetic Programming research system (Java)
- Lil-Gp Genetic Programming System (C).
- Beagle - Open BEAGLE, a versatile EC framework (C++ with STL)
- EO Evolutionary Computation Framework (C++ with static polymorphism)
Others:
- RobGP - Robust Genetic Programming System (C++)
- JEF - JAVA Evolution Framework (Java)
- GPC++ - Genetic Programming C++ Class Library (C++)
- TinyGP (C and Java)
- GenPro - Reflective Object Oriented Genetic Programming Open Source Framework. Extend with POJO's, generates plain Java code. (Java)
- deap Distributed Evolutionary Algorithms in Python (Python)
- pySTEP pySTEP or Python Strongly Typed gEnetic Programming
- Pyevolve (Python)
- JAGA - Extensible and pluggable open source API for implementing genetic algorithms and genetic programming applications (Java)
- RMIT GP - A Genetic Programming Package with support for Automatically Defined Functions (C++)
- GPE - Framework for conducting experiments in Genetic Programming (.NET)
- lalena.com - A Genetic Program for simulating ant food collection behaviors. Free download (.NET)
- DGPF - simple Genetic Programming research system (Java)
- JGAP - Java Genetic Algorithms and Genetic Programming, an open-source framework (Java)
- n-genes - Java Genetic Algorithms and Genetic Programming (stack oriented) framework (Java)
- PMDGP - object oriented framework for solving genetic programming problems (C++)
- DRP - Directed Ruby Programming, Genetic Programming & Grammatical Evolution Library (Ruby)
- GPLAB - A Genetic Programming Toolbox for MATLAB (MATLAB)
- GPTIPS - Genetic Programming Tool for MATLAB - aimed at performing multigene symbolic regression (MATLAB)
- PyRobot - Evolutionary Algorithms (GA + GP) Modules, Open Source (Python)
- PerlGP - Grammar-based genetic programming in Perl (Perl)
- Discipulus - Commercial Genetic Programming Software from RML Technologies, Inc (Generates code in most high level languages)
- GAlib - Object oriented framework with 4 different GA implementations and 4 representation types (arbitrary derivations possible) (C++)
- Java GALib - Source Forge open source Java genetic algorithm library, complete with Javadocs and examples (see bottom of page) (Java)
- LAGEP. Supporting single/multiple population genetic programming to generate mathematical functions. Open Source, OpenMP used. (C/C++)
- PushGP, a strongly typed, stack-based genetic programming system that allows GP to manipulate its own code (auto-constructive evolution) (Java/C++/Javascript/Scheme/Clojure/Lisp)
- Groovy Java Genetic Programming (Java)
- GEVA - Grammatical Evolution in Java (Java)
- jGE - Java Grammatical Evolution (Java)
- ECF - Evolutionary Computation Framework (C++) different genotypes, parallel algorithms, tutorial
- JCLEC - Evolutionary Computation Library in Java (Java) expression tree encoding, syntax tree encoding
See also
- Bio-inspired computing
- Gene expression programming
- Genetic representation
- Grammatical evolution
- Fitness approximation
- Linear genetic programming
References and notes
- ^ Intelligent machinery. Report for National Physical Laboratory. 1948.
- ^ AI, where it has been and where it is going. In IJCAI, pages 1152-1157, 1983.
- ^ A Field Guide to Genetic Programming
- ^ A Field Guide to Genetic Programming
- ^ Genetic Programming
- ^ Genetic Algorithms in Search Optimization and Machine Learning
- ^ Genetic Programming
- ^ Angeline, Subtree crossover: Building block engine or macromutation?, GP 1997, p9-17
- ^ Goldberg, Genetic Algorithms in Search Optimization and Machine Learning, 1989
- ^ Deb. Multi-objective optimization using evolutionary algorithms, 2001
- ^ Nichael Cramer's HomePage
- ^ genetic-programming.com-Home-Page
- ^ humancompetitive
- ^ Cramer, 1985
- ^ (Peter Nordin, 1997, Banzhaf et al., 1998, Section 11.6.2-11.6.3)
- ^ MicroGP page from CAD Group, Politecnico di Torino
- ^ 1987 THESIS ON LEARNING HOW TO LEARN, METALEARNING, META GENETIC PROGRAMMING, CREDIT-CONSERVING MACHINE LEARNING ECONOMY
Bibliography
- Banzhaf, W., Nordin, P., Keller, R.E., and Francone, F.D. (1998), Genetic Programming: An Introduction: On the Automatic Evolution of Computer Programs and Its Applications, Morgan Kaufmann
- Barricelli, Nils Aall (1954), Esempi numerici di processi di evoluzione, Methodos, pp. 45–68.
- Brameier, M. and Banzhaf, W. (2007), Linear Genetic Programming, Springer, New York
- Crosby, Jack L. (1973), Computer Simulation in Genetics, John Wiley & Sons, London.
- Cramer, Nichael Lynn (1985), "A representation for the Adaptive Generation of Simple Sequential Programs" in Proceedings of an International Conference on Genetic Algorithms and the Applications, Grefenstette, John J. (ed.), Carnegie Mellon University
- Fogel, David B. (2000) Evolutionary Computation: Towards a New Philosophy of Machine Intelligence IEEE Press, New York.
- Fogel, David B. (editor) (1998) Evolutionary Computation: The Fossil Record, IEEE Press, New York.
- Forsyth, Richard (1981), BEAGLE A Darwinian Approach to Pattern Recognition Kybernetes, Vol. 10, pp. 159–166.
- Fraser, Alex S. (1957), Simulation of Genetic Systems by Automatic Digital Computers. I. Introduction. Australian Journal of Biological Sciences vol. 10 484-491.
- Fraser, Alex and Donald Burnell (1970), Computer Models in Genetics, McGraw-Hill, New York.
- Holland, John H (1975), Adaptation in Natural and Artificial Systems, University of Michigan Press, Ann Arbor
- Korns, Michael (2007), Large-Scale, Time-Constrained, Symbolic Regression-Classification, in Genetic Programming Theory and Practice V. Springer, New York.
- Korns, Michael (2009), Symbolic Regression of Conditional Target Expressions, in Genetic Programming Theory and Practice VII. Springer, New York.
- Korns, Michael (2010), Abstract Expression Grammar Symbolic Regression, in Genetic Programming Theory and Practice VIII. Springer, New York.
- Koza, J.R. (1990), Genetic Programming: A Paradigm for Genetically Breeding Populations of Computer Programs to Solve Problems, Stanford University Computer Science Department technical report STAN-CS-90-1314. A thorough report, possibly used as a draft to his 1992 book.
- Koza, J.R. (1992), Genetic Programming: On the Programming of Computers by Means of Natural Selection, MIT Press
- Koza, J.R. (1994), Genetic Programming II: Automatic Discovery of Reusable Programs, MIT Press
- Koza, J.R., Bennett, F.H., Andre, D., and Keane, M.A. (1999), Genetic Programming III: Darwinian Invention and Problem Solving, Morgan Kaufmann
- Koza, J.R., Keane, M.A., Streeter, M.J., Mydlowec, W., Yu, J., Lanza, G. (2003), Genetic Programming IV: Routine Human-Competitive Machine Intelligence, Kluwer Academic Publishers
- Langdon, W. B., Genetic Programming and Data Structures, Springer ISBN 0-7923-8135-1
- Langdon, W. B., Poli, R. (2002), Foundations of Genetic Programming, Springer-Verlag ISBN 3-540-42451-2
- Nordin, J.P., (1997) Evolutionary Program Induction of Binary Machine Code and its Application. Krehl Verlag, Muenster, Germany.
- Poli, R., Langdon, W. B., McPhee, N. F. (2008). A Field Guide to Genetic Programming. Lulu.com, freely available from the internet. ISBN 978-1-4092-0073-4.
{{cite book}}: External link in|publisher= - Rechenberg, I. (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis). Reprinted by Fromman-Holzboog (1973).
- Schmidhuber, J. (1987). Evolutionary principles in self-referential learning. (On learning how to learn: The meta-meta-... hook.) Diploma thesis, Institut f. Informatik, Tech. Univ. Munich.
- Smith, S.F. (1980), A Learning System Based on Genetic Adaptive Algorithms, PhD dissertation (University of Pittsburgh)
- Smith, Jeff S. (2002), Evolving a Better Solution, Developers Network Journal, March 2002 issue
- Shu-Heng Chen et al. (2008), Genetic Programming: An Emerging Engineering Tool,International Journal of Knowledge-based Intelligent Engineering System, 12(1): 1-2, 2008.
- Weise, T, Global Optimization Algorithms: Theory and Application, 2008
External links
- DigitalBiology.NET Vertical search engine for GA/GP resources
- Genetic Programming Source a website with a visual beginner's guide to GP.
- Aymen S Saket & Mark C Sinclair
- The Hitch-Hiker's Guide to Evolutionary Computation
- GP bibliography
- People who work on GP
