Stern–Gerlach experiment: Difference between revisions
Nslavov.mit (talk | contribs) m streamlined a long and awkward sentence. |
added commas to make understanding hopefully easier |
||
| Line 27: | Line 27: | ||
Electrons are [[spin-½|spin-{{frac|1|2}}]] particles. These have only two possible spin angular momentum values measured along any axis, +ħ/2 or −ħ/2, a sheerly quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles). |
Electrons are [[spin-½|spin-{{frac|1|2}}]] particles. These have only two possible spin angular momentum values measured along any axis, +ħ/2 or −ħ/2, a sheerly quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles). |
||
For electrons there are two possible values for the spin angular momentum that is measured along an axis. The same is true for the [[proton]] and the [[neutron]], which are composite particles made up of three [[quarks]] each (which are themselves [[spin-½|spin-{{frac|1|2}}]] particles. However the three quarks do not consist of a pair that cancel each other out and a third quark that gives the net {{frac|1|2}} spin to the composite particle as previously believed before the [[Proton spin crisis]] was discovered. Hence the intrinsic spin of the nucleons is orbital rather than intrinsic.). Other particles have a different number of possible spin values. [[Delta baryon]]s ({{SubatomicParticle|Delta++}}, {{SubatomicParticle|Delta+}}, {{SubatomicParticle|Delta0}}, {{SubatomicParticle|Delta-}}), for example, are spin +{{frac|3|2}} particles and have four possible spin momentum values. [[Vector mesons]], as well as [[W and Z bosons]] are spin-1 particles that have three possible spin angular momentum values. |
For electrons there are two possible values for the spin angular momentum that is measured along an axis. The same is true for the [[proton]] and the [[neutron]], which are composite particles made up of three [[quarks]] each (which are themselves [[spin-½|spin-{{frac|1|2}}]] particles. However, the three quarks do not consist of a pair that cancel each other out and a third quark that gives the net {{frac|1|2}} spin to the composite particle, as previously believed before the [[Proton spin crisis]] was discovered. Hence the intrinsic spin of the nucleons is orbital rather than intrinsic.). Other particles have a different number of possible spin values. [[Delta baryon]]s ({{SubatomicParticle|Delta++}}, {{SubatomicParticle|Delta+}}, {{SubatomicParticle|Delta0}}, {{SubatomicParticle|Delta-}}), for example, are spin +{{frac|3|2}} particles and have four possible spin momentum values. [[Vector mesons]], as well as [[W and Z bosons]] are spin-1 particles that have three possible spin angular momentum values. |
||
To describe the experiment with spin +{{frac|1|2}} particles mathematically, it is easiest to use [[Paul Adrien Maurice Dirac|Dirac]]'s [[bra–ket notation]]. As the particles pass through the Stern–Gerlach device, they are being observed by the detector which resolves to either spin up or spin down. These are described by the angular momentum quantum number ''j'', which can take on one of the two possible allowed values, either +ħ/2 or −ħ/2. The act of observing (measuring) the momentum along the z axis corresponds to the operator ''J''<sub>z</sub>. In mathematical terms, |
To describe the experiment with spin +{{frac|1|2}} particles mathematically, it is easiest to use [[Paul Adrien Maurice Dirac|Dirac]]'s [[bra–ket notation]]. As the particles pass through the Stern–Gerlach device, they are being observed by the detector which resolves to either spin up or spin down. These are described by the angular momentum quantum number ''j'', which can take on one of the two possible allowed values, either +ħ/2 or −ħ/2. The act of observing (measuring) the momentum along the z axis corresponds to the operator ''J''<sub>z</sub>. In mathematical terms, |
||
Revision as of 19:11, 21 July 2013
| Part of a series of articles about |
| Quantum mechanics |
|---|
The Stern–Gerlach experiment,[1] named after German physicists Otto Stern and Walther Gerlach, is an important experiment in quantum mechanics on the deflection of particles. This experiment, performed in 1922, is often used to illustrate basic principles of quantum mechanics. It can be used to demonstrate that electrons and atoms have intrinsically quantum properties, and how measurement in quantum mechanics affects the system being measured.
Basic theory and description

The Stern–Gerlach experiment involves sending a beam of particles through an inhomogeneous magnetic field and observing their deflection. The results show that particles possess an intrinsic angular momentum that is closely analogous to the angular momentum of a classically spinning object, but that takes only certain quantized values. Another important result is that only one component of a particle's spin can be measured at one time, meaning that the measurement of the spin along the z-axis destroys information about a particle's spin along the x and y axis.
The experiment is normally conducted using electrically neutral particles or atoms. This avoids the large deflection to the orbit of a charged particle moving through a magnetic field and allows spin-dependent effects to dominate. If the particle is treated as a classical spinning dipole, it will precess in a magnetic field because of the torque that the magnetic field exerts on the dipole (see torque-induced precession). If it moves through a homogeneous magnetic field, the forces exerted on opposite ends of the dipole cancel each other out and the trajectory of the particle is unaffected. However, if the magnetic field is inhomogeneous then the force on one end of the dipole will be slightly greater than the opposing force on the other end, so that there is a net force which deflects the particle's trajectory. If the particles were classical spinning objects, one would expect the distribution of their spin angular momentum vectors to be random and continuous. Each particle would be deflected by a different amount, producing some density distribution on the detector screen. Instead, the particles passing through the Stern–Gerlach apparatus are deflected either up or down by a specific amount. This was a measurement of the quantum observable now known as spin, which demonstrated possible outcomes of a measurement where the observable has point spectrum. Although some discrete quantum phenomena, such as atomic spectra, were observed much earlier, the Stern–Gerlach experiment allowed scientists to conduct measurements of deliberately superposed quantum states for the first time in the history of science.
By now it is known theoretically that quantum angular momentum of any kind has a discrete spectrum, which is sometimes imprecisely expressed as "angular momentum is quantized".
If the experiment is conducted using charged particles like electrons, there will be a Lorentz force that tends to bend the trajectory in a circle (see cyclotron motion). This force can be cancelled by an electric field of appropriate magnitude oriented transverse to the charged particle's path.

Electrons are spin-1⁄2 particles. These have only two possible spin angular momentum values measured along any axis, +ħ/2 or −ħ/2, a sheerly quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles).
For electrons there are two possible values for the spin angular momentum that is measured along an axis. The same is true for the proton and the neutron, which are composite particles made up of three quarks each (which are themselves spin-1⁄2 particles. However, the three quarks do not consist of a pair that cancel each other out and a third quark that gives the net 1⁄2 spin to the composite particle, as previously believed before the Proton spin crisis was discovered. Hence the intrinsic spin of the nucleons is orbital rather than intrinsic.). Other particles have a different number of possible spin values. Delta baryons (
Δ++
,
Δ+
,
Δ0
,
Δ−
), for example, are spin +3⁄2 particles and have four possible spin momentum values. Vector mesons, as well as W and Z bosons are spin-1 particles that have three possible spin angular momentum values.
To describe the experiment with spin +1⁄2 particles mathematically, it is easiest to use Dirac's bra–ket notation. As the particles pass through the Stern–Gerlach device, they are being observed by the detector which resolves to either spin up or spin down. These are described by the angular momentum quantum number j, which can take on one of the two possible allowed values, either +ħ/2 or −ħ/2. The act of observing (measuring) the momentum along the z axis corresponds to the operator Jz. In mathematical terms,
- .
The constants c1 and c2 are complex numbers. The squares of their absolute values (|c1|2 and |c2|2) determine the probabilities that in the state one of the two possible values of j is found. The constants must also be normalized in order that the probability of finding either one of the values be unity. However, this information is not sufficient to determine the values of c1 and c2, because they may in fact be complex numbers. Therefore the measurement yields only the absolute values of the constants.
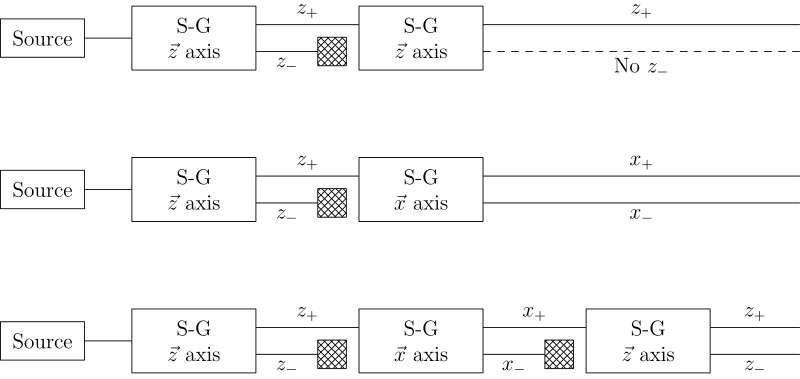
Sequential experiments
If we link multiple Stern–Gerlach apparatuses, we can clearly see that they do not act as simple selectors, but alter the states observed (as in light polarization), according to quantum mechanical law: [2]
History

The Stern–Gerlach experiment was performed in Frankfurt, Germany in 1922 by Otto Stern and Walther Gerlach. At the time, Stern was an assistant to Max Born at the University of Frankfurt's Institute for Theoretical Physics, and Gerlach was an assistant at the same university's Institute for Experimental Physics.
At the time of the experiment, the most prevalent model for describing the atom was the Bohr model, which described electrons as going around the positively charged nucleus only in certain discrete atomic orbitals or energy levels. Since the electron was quantized to be only in certain positions in space, the separation into distinct orbits was referred to as space quantization. The Stern–Gerlach experiment was meant to test the Bohr–Sommerfeld hypothesis that the direction of the angular momentum of a silver atom is quantized.[3]
Note that the experiment was performed several years before Uhlenbeck and Goudsmit formulated their hypothesis of the existence of the electron spin. Even though the result of the Stern−Gerlach experiment has later turned out to be in agreement with the predictions of quantum mechanics for a spin-1⁄2 particle, the experiment should be seen as a corroboration of the Bohr–Sommerfeld theory.[4]
In 1927, T.E. Phipps and J.B. Taylor reproduced the effect using hydrogen atoms in their ground state, thereby eliminating any doubts that may have been caused by the use of silver atoms.[5] (In 1926 the non-relativistic Schrödinger equation had incorrectly predicted the magnetic moment of hydrogen to be zero in its ground state. To correct this problem Wolfgang Pauli introduced "by hand", so to speak, the 3 Pauli matrices which now bear his name, but which were later shown by Paul Dirac in 1928 to be intrinsic in his relativistic equation.)[6]
Importance
The Stern–Gerlach experiment strongly influenced later developments in modern physics:
- In the decade that followed, scientists showed using similar techniques, that the nuclei of some atoms also have quantized angular momentum. It is the interaction of this nuclear angular momentum with the spin of the electron that is responsible for the hyperfine structure of the spectroscopic lines.
- In the 1930s, using an extended version of the Stern–Gerlach apparatus, Isidor Rabi and colleagues showed that by using a varying magnetic field, one can force the magnetic momentum to go from one state to the other. The series of experiments culminated in 1937 when they discovered that state transitions could be induced using time varying fields or RF fields. The so called Rabi oscillation is the working mechanism for the Magnetic Resonance Imaging equipment found in hospitals.
- Norman F. Ramsey later modified the Rabi apparatus to increase the interaction time with the field. The extreme sensitivity due to the frequency of the radiation makes this very useful for keeping accurate time, and it is still used today in atomic clocks.
- In the early sixties, Ramsey and Daniel Kleppner used a Stern–Gerlach system to produce a beam of polarized hydrogen as the source of energy for the hydrogen Maser, which is still one of the most popular atomic clocks.
- The direct observation of the spin is the most direct evidence of quantization in quantum mechanics.
- The Stern–Gerlach experiment has become a paradigm of quantum measurement. In particular, it has been assumed to satisfy von Neumann projection. According to more recent insights, based on a quantum mechanical description of the influence of the inhomogeneous magnetic field,[7] this can be true only in an approximate sense. Von Neumann projection can be rigorously satisfied only if the magnetic field is homogeneous. Hence, von Neumann projection is even incompatible with a proper functioning of the Stern–Gerlach device as an instrument for measuring spin.
See also
References
- ^ Gerlach, W.; Stern, O. (1922). "Das magnetische Moment des Silberatoms". Zeitschrift für Physik. 9: 353–355. Bibcode:1922ZPhy....9..353G. doi:10.1007/BF01326984.
- ^ Sakurai, J.-J. (1985). Modern quantum mechanics. Addison-Wesley. ISBN 0-201-53929-2.
- ^ Stern, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik. 7: 249–253. Bibcode:1921ZPhy....7..249S. doi:10.1007/BF01332793.
- ^ Weinert, F. (1995). "Wrong theory—right experiment: The significance of the Stern–Gerlach experiments". Studies in History and Philosophy of Modern Physics. 26B: 75−86. doi:10.1016/1355-2198(95)00002-B.
- ^ Phipps, T.E.; Taylor, J.B. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review. 29 (2): 309–320. Bibcode:1927PhRv...29..309P. doi:10.1103/PhysRev.29.309.
- ^ A., Henok (2002). Introduction to Applied Modern Physics. Lulu.com. p. 76. ISBN 1-4357-0521-1.
- ^ Scully, M.O.; Lamb, W.E.; Barut, A. (1987). "On the theory of the Stern–Gerlach apparatus". Foundations of Physics. 17 (6): 575–583. Bibcode:1987FoPh...17..575S. doi:10.1007/BF01882788.
External links
- Animation, applications and research linked to the spin (Université Paris Sud)
Further reading
- Friedrich, B.; Herschbach, D. (2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics". Physics Today. 56 (12): 53. Bibcode:2003PhT....56l..53F. doi:10.1063/1.1650229.
- Reinisch, G. (1999). "Stern–Gerlach experiment as the pioneer—and probably the simplest—quantum entanglement test?". Physics Letters A. 259 (6): 427–430. Bibcode:1999PhLA..259..427R. doi:10.1016/S0375-9601(99)00472-7.
- Venugopalan, A. (1997). "Decoherence and Schrödinger-cat states in a Stern−Gerlach-type experiment". Physical Review A. 56 (5): 4307–4310. Bibcode:1997PhRvA..56.4307V. doi:10.1103/PhysRevA.56.4307.
- Hsu, B.; Berrondo, M.; Van Huele, J.-F. (2011). "Stern-Gerlach dynamics with quantum propagators". Physical Review A. 83 (1): 012109-1-12. Bibcode:2011PhRvA..83a2109H. doi:10.1103/PhysRevA.83.012109.
- Jeremy Bernstein (2010). "The Stern Gerlach Experiment". arXiv:1007.2435v1 [physics.hist-ph].
- Use of ions



