Energy minimization

"Geometry optimization" redirects here. For the method in optimal control theory, see Shape optimization.

In the field of computational chemistry, energy minimization (also called energy optimization or geometry optimization) is the process of finding an arrangement in space of a collection of atoms where the forces acting on the atoms are (very close to) zero. This zero-force configuration is often referred to as the equilibrium configuration (or geometry). The collection of atoms might be a single molecule molecule, an ion, a condensed phase, a transition state or even a collection of any of these.

Typically (but not always) the process seeks to find the geometry of a particular arrangement of the atoms that represents a local energy minimum.

Given a set of atoms and a vector, r, describing the atoms' positions, one can introduce the concept of the energy as a function of the positions, E(r). The energy minimization procedure is then a mathematical optimization problem, in which it is desired to find the value of r for which E(r) is at a local minimum.

A helpful concept is the potential energy surface (PES) of a set of atoms and this is the surface formed by E(r) . Stable states of molecular systems correspond to minima on the potential energy surface.

Various techniques e.g. quantum mechanics are able to provide an estimate of E(r) and ideally also the gradient of the PES, that is, the derivative of the energy with respect to the position of the atoms, ∂E/∂r.

Concept of molecular geometry

As stated in the introduction, the geometry of a set of atoms is the vector describing the atoms' positions. This could be the set of the Cartesian coordinates of the atoms or, when considering molecules, might be internal coordinates formed from a set of bond lengths, bond angles and dihedral angles. The choice of the coordinate system can be crucial for performing a successful optimization. Cartesian coordinates, for example, are redundant and highly correlated.

Variations and techniques

When the gradient of the energy can be computed, far more efficient optimization is possible. If the energy gradient cannot be computed directly, it is often estimated numerically. If it is too computationally expensive to calculate the gradient analytically, different optimization methods might be used that do not require the gradient, such as the Powell's direction set method or the downhill simplex method can generally be more efficient than the gradient methods.

Simple gradient method

See also: Gradient descent

Here we have a single function of the potential energy to minimize with 3N independent variables, which are the 3 components of the coordinates of N atoms in our system. We calculate the net force on each atom F at each iteration step t, and we move the atoms in the direction of F with a multiple factor k. k can be smaller at the beginning of calculation if we begin with a very high potential energy. Note that similar strategy can be used in molecular dynamics for reducing the probability of divergence problems at the beginning of simulations.

$r_{i}^{t}=r_{i}^{t-1}+\kappa \cdot F\left(r_{i}\right),\quad i=1,\ldots ,N.$

We repeat this step in the above equation t = 1,2,... until F reaches zero for every atom. The potential energy of system goes down in a long narrow valley of energy in this procedure.

Though it is also called “steepest descent”, the simple gradient algorithm is in fact very time-consuming if we compare it to the nonlinear conjugate gradient approach; it is therefore known as a not very good algorithm. However, its advantage is its numerical stability, i.e., the potential energy can never increase if we take a reasonable k. Thus, it can be combined with a conjugated gradient algorithm for solving the numerical divergence problem when two atoms are too close to each other.

Nonlinear conjugate gradient method

See also: Nonlinear conjugate gradient method

The conjugate gradient algorithm includes two basic steps: adding an orthogonal vector to the current direction of the search, and then move them in another direction nearly perpendicular to this vector. These two steps are also known as: step on the valley floor and then jump down. Figure 2 shows a highly simplified comparison between the conjugate and the simple gradient methods on a 1D energy curve.

Figure 2: Comparison between two gradient algorithms on a simple 1D energy curve.

In this algorithm, we minimize the energy function by moving the atoms as follows,

$r_{i}^{t}=r_{i}^{t-1}+\kappa \cdot h_{i}^{t-1},\quad i=1,\ldots ,N$

where

$h_{i}^{t}=F\left(r_{i}^{t}\right)+\gamma _{i}^{t}h_{i}^{t-1}$

and gamma is updated using the Fletcher-Reeves formula as:

$\gamma _{i}^{t}={\frac {F\left(r_{i}^{t}\right)\cdot F\left(r_{i}^{t}\right)}{F\left(r_{i}^{t-1}\right)\cdot F\left(r_{i}^{t-1}\right)}}$

Here we note that gamma can also be calculated by using the Polak-Ribiere formula, however, it is less efficient than the Fletcher-Reeves one for certain energy functions. At the beginning of calculation (when t = 1), we can make the search direction vector 'h0 = 0.

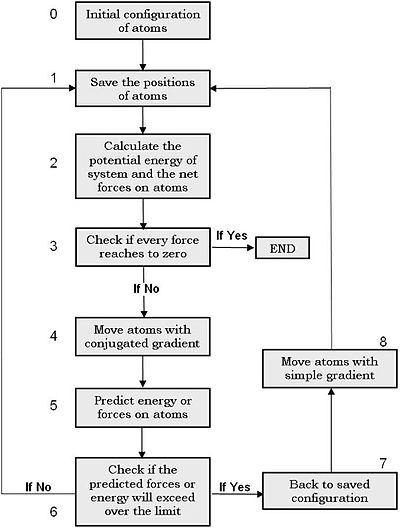
This algorithm is very efficient. However, it is not quite stable with certain potential functions, i.e. it sometimes can step so far into a very strong repulsive energy range (e.g. when two atoms are too close to each other), where the gradient at this point is almost infinite. It can directly result a typical data-overrun error during the calculation. To resolve this problem, we can combine the conjugate gradient algorithm with the simple one. Figure 3 shows the schematics of the combined algorithm. We note for implementation that steps 2 and 5 can be combined into a single step

Figure 3: Schematics of a computational energy minimization procedure.

Boundary conditions

The atoms in our system can have different degrees of freedom. For example, in case of a tube suspended over two supports, we need to fix certain number of atoms N* at the tube ends during the calculation. In this case, it is enough not to move these N* atoms in the step 4 or 8 in Figure 3, but we still calculate their interaction with other atoms in the steps 2 and 5. i.e. from mathematical point of view, we change the total number of variables in the energy function from 3N to 3N-3N*using the boundary condition, by which the values of these 3N* unknown variables are taken as known constants. Note that one can even fix atoms in only one or two directions in this way.

Moreover, one can equally adding other boundary conditions to the minimized energy function, such as adding external forces or external electric fields to the system. In these cases, the terms in potential energy function will be changed but the number of variables remains constant.

Here an example of the application of the energy minimization method in molecular modeling in nanoscience is shown in Figure 4.

Figure 4: Electrostatic deflections of a carbon nanotube in an electric field.

Further information about the application of this method in nanoscience and Computational Codes programmed in Fortran for students is available in the following external links.

Comparison with techniques

Unlike molecular dynamics simulations, which are based on Newtonian dynamic laws and allow calculation of atomic trajectories with kinetic energy, molecular energy minimization does not include the effect of temperature, and hence the trajectories of atoms during the calculation do not really make any physical sense, i.e. we can only obtain a final state of system that corresponds to a local minimum of potential energy. From a physical point of view, this final state of the system corresponds to the configuration of atoms when the temperature of the system is approximately zero, e.g. as shown in Figure 1, if there is a cantilevered beam vibrating between positions 1 and 2 around an equilibrium position 0 with an initial kinetic motion, whether we start with the state 1, the state 2 or any other state between these two positions, the result of energy minimization for this system will always be the state 0.

See also

• Graph cuts in computer vision – apparatus for solving computer vision problems that can be formulated in terms of energy minimization
• Energy principles in structural mechanics

External links

• Numerical Recipes in Fortran 77

Additional references

• Payne et al., "Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients", Reviews of Modern Physics 64 (4), pp. 1045–1097. (1992) (abstract)
• Atich et al., "Conjugate gradient minimization of the energy functional: A new method for electronic structure calculation", Physical Review B 39 (8), pp. 4997–5004, (1989)
• Chadi, "Energy-minimization approach to the atomic geometry of semiconductor surfaces", Physical Review Letters 41 (15), pp. 1062–1065 (1978)