Cube root

In mathematics, a cube root of a number, denoted ${\sqrt[{3}]{x}}$ or x^1/3, is a number a such that a³ = x. All real numbers have exactly one real cube root and a pair of complex conjugate roots, and all nonzero complex numbers have three distinct complex cube roots. For example, the real cube root of 8 is 2, because 2³ = 8. All the cube roots of −27i are

{\sqrt[{3}]{-27i}}={\begin{cases}3i\\{\frac {3{\sqrt {3}}}{2}}-{\frac {3}{2}}i\\-{\frac {3{\sqrt {3}}}{2}}-{\frac {3}{2}}i\end{cases}}

The cube root operation is not associative or distributive with addition or subtraction.

The cube root operation is associative with exponentiation and distributive with multiplication and division if consider only real numbers, but not always if consider complex number, for example:

({\sqrt[{3}]{8}})^{3}=8

but

{\sqrt[{3}]{8^{3}}}={\begin{cases}\ \ 8\\-4+4{\sqrt {3}}i\\-4-4{\sqrt {3}}i\end{cases}}

Formal definition

The cube roots of a number x are the numbers y which satisfy the equation

y^{3}=x.

Real numbers

If x and y are real, then there is a unique solution and so the cube root of a real number is sometimes defined by this equation. If this definition is used, the cube root of a negative number is a negative number. The principal cube root of x is also represented by

{\sqrt[{3}]{x}}=x^{1 \over 3}.

If x and y are allowed to be complex, then there are three solutions (if x is non-zero) and so x has three cube roots. A real number has one real cube root and two further cube roots, which form a complex conjugate pair. This can lead to some interesting results.

For instance, the cube roots of the number one are:

{\sqrt[{3}]{1}}={\begin{cases}\ \ 1\\-{\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i\\-{\frac {1}{2}}-{\frac {\sqrt {3}}{2}}i\end{cases}}

These two roots lead to a relationship between all roots. If a number is one cube root of any real or complex number, the other two cube roots can be found by multiplying that number by the two complex cube roots of one.

Complex numbers

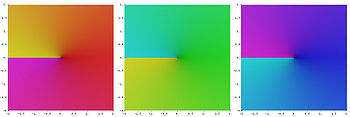
For complex numbers, the principal cube root is usually defined by

x^{1 \over 3}=\exp \left({\ln {x} \over 3}\right)

where ln(x) is the principal branch of the natural logarithm. If we write x as

x=r\exp(i\theta )\,

where r is a non-negative real number and θ lies in the range

-\pi <\theta \leq \pi

,

then the complex cube root is

{\sqrt[{3}]{x}}={\sqrt[{3}]{r}}\exp \left({i\theta  \over 3}\right)

.

This means that in polar coordinates, we are taking the cube root of the radius and dividing the polar angle by three in order to define a cube root. With this definition, the cube root of a negative number is a complex number, and for instance ${\sqrt[{3}]{-8}}$ will not be $-2$ , but rather $1+i{\sqrt {3}}$ .

This limitation can easily be avoided if we write the original complex number x in three equivalent forms, namely

x=r\exp(i\theta )\,

,

r\exp(i(\theta +2\pi ))\,

or

r\exp(i(\theta -2\pi ))\,

.

The three complex cube roots are then

{\sqrt[{3}]{x}}={\sqrt[{3}]{r}}\exp \left({i\theta  \over 3}\right)

,

{\sqrt[{3}]{r}}\exp \left(i\left({\theta  \over 3}+{2\pi  \over 3}\right)\right)

or

{\sqrt[{3}]{r}}\exp \left(i\left({\theta  \over 3}-{2\pi  \over 3}\right)\right)

.

In general, these three complex numbers are distinct, even though the three representations of x were the same. For example, ${\sqrt[{3}]{-8}}$ may then be calculated to be $1+i{\sqrt {3}}$ , $-2$ or $1-i{\sqrt {3}}$ .

In programs that are aware of the imaginary plane, the graph of the cube root of x on the real plane will not display any output for negative values of x. To also include negative roots, these programs must be explicitly instructed to only use real numbers. (In Mathematica, this can be achieved by executing the following line <<Miscellaneous`RealOnly`.)

Cube root on a standard calculator

From the identity:

{\frac {1}{3}}={\frac {1}{2^{2}}}\left(1+{\frac {1}{2^{2}}}\right)\left(1+{\frac {1}{2^{4}}}\right)\left(1+{\frac {1}{2^{8}}}\right)\left(1+{\frac {1}{2^{16}}}\right)\dots

,

there is a simple method to compute the cube roots using a non-scientific calculator, which requires only the multiplication and square root buttons. No memory is required. The following method is used:

Press the square root button twice.
Press the multiplication button.
Press the square root button twice.
Press the multiplication button.
Press the square root button four times.
Press the multiplication button.
Press the square root button eight times.
Press the multiplication button...

This process is continued until the number does not change when the multiplication button is pressed, since the repeated square root gives 1 (this means that the solution has been determined to as many significant digits as the calculator can handle). At this point an approximation of the cube root of the original number will be shown in the display.

If the first multiplication is replaced by division, instead of the cube root, the fifth root will be shown on the display.

Why this method works

After raising x to the power on both sides of the above identity:

x^{\frac {1}{3}}=x^{{\frac {1}{2^{2}}}\left(1+{\frac {1}{2^{2}}}\right)\left(1+{\frac {1}{2^{4}}}\right)\left(1+{\frac {1}{2^{8}}}\right)\left(1+{\frac {1}{2^{16}}}\right)...}

(*)

The left hand side is the cube root of x.

The steps shown in the method give:

After the second step:

x^{\frac {1}{2^{2}}}

After the fourth step:

x^{{\frac {1}{2^{2}}}(1+{\frac {1}{2^{2}}})}

After the sixth step:

x^{{\frac {1}{2^{2}}}(1+{\frac {1}{2^{2}}})(1+{\frac {1}{2^{4}}})}

After the eighth step:

x^{{\frac {1}{2^{2}}}(1+{\frac {1}{2^{2}}})(1+{\frac {1}{2^{4}}})(1+{\frac {1}{2^{8}}})}

etc.

Once the value of the expression is equal to 1 to the accuracy of the calculator, the final square root will return the right hand of (*).

External links

Template:Link FA