Area
This article needs additional citations for verification. (May 2009) |
Area is a quantity expressing the two-dimensional size of a defined part of a surface, typically a region bounded by a closed curve. The term surface area refers to the total area of the exposed surface of a 3-dimensional solid, such as the sum of the areas of the exposed sides of a polyhedron. Area is an important invariant in the differential geometry of surfaces.
Units
Units for measuring area include:
- area (a) = 100 square meters (m²)
- hectare (ha) = 100 ares (a) = 10000 square meters (m²)
- square kilometre (km²) = 100 hectars (ha) = 10000 ares (a) = 1000000 square metres (m²)
- square megametre (Mm²) = 1012 square metres
- square foot = 144 square inches = 0.09290304 square metres (m²)
- square yard = 9 square feet (0.84 m2) = 0.83612736 square metres (m²)
- square perch = 30.25 square yards = 25.2928526 square metres (m²)
- acre = 10 square chains (also one furlong by one chain); or 160 square perches; or 4840 square yards; or 43,560 square feet (4,047 m2) = 4046.8564224 square metres (m²)
- square mile = 640 acres (2.6 km2) = 2.5899881103 square kilometers (km²)
Formulæ
| Shape | Equation | Variables |
|---|---|---|
| Square | is the length of one side of the square. | |
| Regular triangle (equilateral triangle) | is the length of one side of the triangle. | |
| Regular hexagon | is the length of one side of the hexagon. | |
| Regular octagon | is the length of one side of the octagon. | |
| Any regular polygon | is the apothem, or the radius of an inscribed circle in the polygon, and is the perimeter of the polygon. | |
| Any regular polygon | is the sidelength and is the number of sides. | |
| Any regular polygon (using degree measure) | is the sidelength and is the number of sides. | |
| Rectangle | and are the lengths of the rectangle's sides (length and width). | |
| Parallelogram (in general) | and are the length of the base and the length of the perpendicular height, respectively. | |
| Rhombus | and are the lengths of the two diagonals of the rhombus. | |
| Triangle | and are the base and altitude (measured perpendicular to the base), respectively. | |
| Triangle | and are any two sides, and is the angle between them. | |
| Circle | is the radius and the diameter. | |
| Ellipse | and are the semi-major and semi-minor axes, respectively. | |
| Trapezoid | and are the parallel sides and the distance (height) between the parallels. | |
| Total surface area of a Cylinder | and are the radius and height, respectively. | |
| Lateral surface area of a cylinder | and are the radius and height, respectively. | |
| Total surface area of a Cone | and are the radius and slant height, respectively. | |
| Lateral surface area of a cone | and are the radius and slant height, respectively. | |
| Total surface area of a Sphere | and are the radius and diameter, respectively. | |
| Total surface area of an ellipsoid | See the article. | |
| Circular sector | and are the radius and angle (in radians), respectively. | |
| Square to circular area conversion | is the area of the square in square units. | |
| Circular to square area conversion | is the area of the circle in circular units. |
The above calculations show how to find the area of many common shapes.
The area of irregular polygons can be calculated using the "Surveyor's formula".[1]
Additional formulæ
Areas of 2-dimensional figures
- a triangle: (where B is any side, and h is the distance from the line on which B lies to the other vertex of the triangle). This formula can be used if the height h is known. If the lengths of the three sides are known then Heron's formula can be used: (where a, b, c are the sides of the triangle, and is half of its perimeter) If an angle and its two included sides are given, then area=absinC where C is the given angle and a and b are its included sides. If the triangle is graphed on a coordinate plane, a matrix can be used and is simplified to the absolute value of (x1y2+ x2y3+ x3y1 - x2y1- x3y2- x1y3) all divided by 2. This formula is also known as the shoelace formula and is an easy way to solve for the area of a coordinate triangle by substituting the 3 points, (x1,y1) (x2,y2) (x3,y 3). The shoelace formula can also be used to find the areas of other polygons when their vertices are known. Another approach for a coordinate triangle is to use Infinitesimal calculus to find the area.
Area in calculus
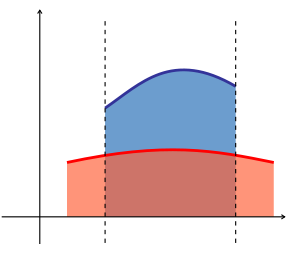
- the area between the graphs of two functions is equal to the integral of one function, f(x), minus the integral of the other function, g(x).
- an area bounded by a function r = r(θ) expressed in polar coordinates is .
- the area enclosed by a parametric curve with endpoints is given by the line integrals
(see Green's theorem)
- or the z-component of
Surface area of 3-dimensional figures
- cube: , where s is the length of the top side
- rectangular box: the length divided by height
- cone: , where r is the radius of the circular base, and h is the height. That can also be rewritten as where r is the radius and l is the slant height of the cone. is the base area while is the lateral surface area of the cone.
- prism: 2 * Area of Base + Perimeter of Base * Height
General formula
The general formula for the surface area of the graph of a continuously differentiable function where and is a region in the xy-plane with the smooth boundary:
Even more general formula for the area of the graph of a parametric surface in the vector form where is a continuously differentiable vector function of :
Area minimisation
Given a wire contour, the surface of least area spanning ("filling") it is a minimal surface. Familiar examples include soap bubbles.
The question of the filling area of the Riemannian circle remains open.
See also
- Equi-areal mapping
- Integral
- Orders of magnitude (area)—A list of areas by size.
- Volume
References
- ^ http://www.maa.org/pubs/Calc_articles/ma063.pdf
- ^ do Carmo, Manfredo. Differential Geometry of Curves and Surfaces. Prentice-Hall, 1976. Page 98.


























































