Euclidean geometry

A Greek mathematician performing a geometric construction with a compass, from The School of Athens by Raphael.

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, whose Elements is the earliest known systematic discussion of geometry. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could be fit into a comprehensive deductive and logical system. The Elements begin with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, couched in geometrical language.

For over two thousand years, the adjective "Euclidean" was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious that any theorem proved from them was deemed true in an absolute sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. It also is no longer taken for granted that Euclidean geometry describes physical space. An implication of Einstein's theory of general relativity is that Euclidean space is a good approximation to the properties of physical space only if the gravitational field is not too strong.

The Elements

Main article: Euclid's Elements

The Elements are mainly a systematization of earlier knowledge of geometry. Its superiority over earlier treatments was rapidly recognized, with the result that there was little interest in preserving the earlier ones, and they are now nearly all lost.

Books I-IV discuss plane geometry. Many results about plane figures are proved, e.g., If a triangle has two equal angles, then the sides subtended by the angles are equal. The Pythagorean theorem is proved.

Books V-X deal with number theory, with numbers treated geometrically via their representation as line segments with various lengths. Notions such as prime numbers and rational and irrational numbers are introduced. The infinitude of prime numbers is proved.

Books XI-XIII concern solid geometry. A typical result is the 1:3 ratio between the volume of a cone and a cylinder with the same height and base.

The parallel postulate: If two lines intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side if extended far enough.

Axioms

Euclidean geometry is an axiomatic system, in which all theorems ("true statements") are derived from a small number of axioms. Near the beginning of the first book of the Elements, Euclid gives five postulates (axioms) for plane geometry, stated in terms of constructions:

1. Let the following be postulated: to draw a straight line from any point to any point.
2. To produce [extend] a finite straight line continuously in a straight line.
3. To describe a circle with any center and distance [radius].
4. That all right angles are equal to one another.
5. The parallel postulate: That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.

Although Euclid's statement of the postulates only explicitly asserts the existence of the constructions, they are also taken to be unique.

The Elements also include the following five "common notions":

1. Things that equal the same thing also equal one another.
2. If equals are added to equals, then the wholes are equal.
3. If equals are subtracted from equals, then the remainders are equal.
4. Things that coincide with one another equal one another.
5. The whole is greater than the part.

The parallel postulate

Main article: Parallel postulate

To the ancients, the parallel postulate seemed less obvious than the others. Euclid himself seems to have considered it as being qualitatively different from the others, as evidenced by the organization of the Elements: the first 28 propositions he presents are those that can be proved without it.

Many alternative axioms can be formulated that have the same logical consequences as the parallel postulate. For example Playfair's axiom states:

Through a point not on a given straight line, at most one line can be drawn that never meets the given line.

A proof from Euclid's elements that, given a line segment, an equilateral triangle exists that includes the segment as one of its sides. The proof is by construction: an equilateral triangle ΑΒΓ is made by drawing circles Δ and Ε centered on the points Α and Β, and taking one intersection of the circles as the third vertex of the triangle.

Methods of proof

Euclidean geometry is constructive. Postulates 1, 2, 3, and 5 assert the existence and uniqueness of certain geometric figures, and these assertions are of a constructive nature: that is, we are not only told that certain things exist, but are also given methods for creating them with no more than a compass and an unmarked straightedge. In this sense, Euclidean geometry is more concrete than many modern axiomatic systems such as set theory, which often assert the existence of objects without saying how to construct them, or even assert the existence of objects that cannot be constructed within the theory. Strictly speaking, the lines on paper are models of the objects defined within the formal system, rather than instances of those objects. For example a Euclidean straight line has no width, but any real drawn line will. Although nonconstructive methods are today considered by nearly all mathematicians to be just as sound as constructive ones, Euclid's constructive proofs often supplanted fallacious nonconstructive ones, e.g., some of the Pythagoreans' proofs involving irrational numbers, which usually required a statement such as "Find the greatest common measure of ..."

Euclid often used proof by contradiction. Euclidean geometry also allows the method of superposition, in which a figure is transferred to another point in space. For example, proposition I.4, side-angle-side congruence of triangles, is proved by moving one of the two triangles so that one of its sides coincides with the other triangle's equal side, and then proving that the other sides coincide as well. Some modern treatments add a sixth postulate, the rigidity of the triangle, which can be used as an alternative to superposition.

System of measurement and arithmetic

Euclidean geometry has two fundamental types of measurements: angle and distance. The angle scale is absolute, and Euclid uses the right angle as his basic unit, so that, e.g., a 45-degree angle would be referred to as half of a right angle. The distance scale is relative; one arbitrarily picks a line with a certain length as the unit, and other distances are expressed in relation to it.

A line in Euclidean geometry is a model of the real number line. Addition is represented by a construction in which one line is copied onto the end of another line to extend its length, and similarly for subtraction.

Measurements of area and volume are derived from distances. For example, a rectangle with a width of 3 and a length of 4 has an area that represents the product, 12. Because this geometrical interpretation of multiplication was limited to three dimensions, there was no direct way of interpreting the product of four or more numbers, and Euclid avoided such products, although they are implied, e.g., in the proof of book IX, proposition 20.

An example of congruence. The two figures on the left are congruent, while the third is similar to them. The last figure is neither. Note that congruences alter some properties, such as location and orientation, but leave others unchanged, like distance and angles. The latter sort of properties are called invariants and studying them is the essence of geometry.

Euclid refers to a pair of lines, or a pair of planar or solid figures, as "equal" (ἴσος) if their lengths, areas, or volumes are equal, and similarly for angles. The stronger term "congruent" refers to the idea that an entire figure is the same size and shape as another figure. Alternatively, two figures are congruent if one can be moved on top of the other so that it matches up with it exactly. (Flipping it over is allowed.) Thus, for example, a 2x6 rectangle and a 3x4 rectangle are equal but not congruent, and the letter R is congruent to its mirror image. Figures that would be congruent except for their differing sizes are referred to as similar.

Notation and terminology

Naming of points and figures

Points are customarily named using capital letters of the alphabet. Other figures, such as lines, triangles, or circles, are named by listing a sufficient number of points to pick them out unambiguously from the relevant figure, e.g., triangle ABC would typically be a triangle with vertices at points A, B, and C.

Complementary and supplementary angles

Angles whose sum is a right angle are called complementary, those whose sum is two right angles supplementary.

Modern versions of Euclid's notation

In modern terminology, angles would normally be measured in degrees or radians.

Modern school textbooks often define separate figures called lines (infinite), rays (semi-infinite), and line segments (of finite length). Euclid, rather than discussing a ray as an object that extends to infinity in one direction, would normally use locutions such as "if the line is extended to a sufficient length," although he occasionally referred to "infinite lines." A "line" in Euclid could be either straight or curved, and he used the more specific term "straight line" when necessary.

Some important or well known results

• The bridge of asses theorem states that A=B and C=D.
  The bridge of asses theorem states that A=B and C=D.
• 
  The sum of angles A, B, and C is equal to 180 degrees.
• 
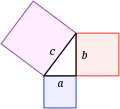
  Pythagoras' theorem: The sum of the areas of the two squares on the legs (a and b) of a right triangle equals the area of the square on the hypotenuse (c).
• 
  Thales' theorem: if AC is a diameter, then the angle at B is a right angle.

The Bridge of Asses

The Bridge of Asses (Pons Asinorum) states that in isosceles triangles the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another. Its name may be attributed to its frequent role as the first real test in the Elements of the intelligence of the reader and as a bridge to the harder propositions that followed. It might also be so named because of the geometrical figure's resemblance to a steep bridge which could only be crossed by a sure–footed donkey.

Congruence of triangles

Congruence of triangles is determined by specifying two sides and the angle between them (SAS), two angles and the side between them (ASA) or two angles and a corresponding adjacent side (AAS). Specifying two sides and an adjacent angle (SSA), however, can yield two distinct possible triangles.

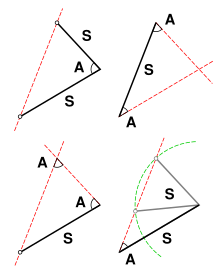
Triangles are congruent if they have all three sides equal (SSS), two sides and the angle between them equal (SAS), or two angles and a side equal (ASA) (Book I, propositions 4, 8, and 26). (Triangles with three equal angles are generally similar, but not necessarily congruent. Also, triangles with two equal sides and an adjacent angle are not necessarily equal.)

Sum of the angles of a triangle

The sum of the angles of a triangle is equal to two right angles (180 degrees).

The Pythagorean theorem

The celebrated Pythagorean theorem (book I, proposition 47) states that in any right triangle, the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares whose sides are the two legs (the two sides that meet at a right angle).

Thales' theorem

Thales' theorem (book I, proposition 32, named after Thales of Miletus) states that if A, B, and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Tradition has it that Thales sacrificed an ox to celebrate this theorem.

Scaling of area and volume

In modern terminology, the area of a plane figure is proportional to the square of any of its linear dimensions, $A\propto L^{2}$, and the volume of a solid to the cube, $V\propto L^{3}$. Euclid proved these results in various special cases such as the area of a circle and the volume of a parallelepipedal solid. Euclid determined some, but not all, of the relevant constants of proportionality. E.g., it was his successor Archimedes who proved that a sphere has 2/3 the volume of the circumscribing cylinder.

Applications

Because of Euclidean geometry's fundamental status in mathematics, it would be impossible to give more than a representative sampling of applications here.

• 
  A surveyor uses a theodolite
• 
  Sphere packing applies to a stack of oranges.
• 
  A parabolic mirror brings parallel rays of light to a focus.

As suggested by the etymology of the word, one of the earliest reasons for interest in geometry was surveying, and certain practical results from Euclidean geometry, such as the right-angle property of the 3-4-5 triangle, were used long before they were proved formally. The fundamental types of measurements in Euclidean geometry are distances and angles, and both of these quantities can be measured directly by a surveyor. Historically, distances were often measured by chains such as Gunter's chain, and angles using graduated circles and, later, the theodolite.

An application of Euclidean solid geometry is the determination of packing arrangements, such as the problem of finding the most efficient packing of spheres in n dimensions. This problem has applications in error detection and correction.

Geometric optics uses Euclidean geometry to analyze the focusing of light by lenses and mirrors.

• 
  Geometry is used in art and architecture.
• 
  The water tower consists of a cone, a cylinder, and a hemisphere. Its volume can be calculated using solid geometry.
• 
  Geometry can be used to design origami.

Geometry is used extensively in architecture.

Geometry can be used to design origami. Some classical construction problems of geometry are impossible using compass and straightedge, but can be solved using origami.

As a description of the structure of space

Euclid believed that his axioms were self-evident statements about physical reality. Taken as a physical description of space, postulate 2 (extending a line) asserts that space does not have holes or boundaries (i.e., space is homogenous); postulate 4 (equality of right angles) says that space is homogeneous and isotropic, so that figures may be moved to any location while maintaining congruence; and postulate 5 that space is flat (has no intrinsic curvature). As discussed in more detail below, Einstein's theory of relativity significantly modifies this view.

The ambiguous character of the axioms as originally formulated by Euclid makes it possible for different commentators to disagree about some of their other implications for the structure of space, such as whether or not it is infinite (see below) and what its topology is. Modern, more rigorous reformulations of the system typically aim for a cleaner separation of these issues. Interpreting Euclid's axioms in the spirit of this more modern approach, axioms 1-4 are consistent with either infinite or finite space (as in elliptic geometry), and all five axioms are consistent with a variety of topologies (e.g., a plane, a cylinder, or a torus for two-dimensional Euclidean geometry).

Later work

Archimedes and Apollonius

A sphere has 2/3 the volume and surface area of its circumscribing cylinder. A sphere and cylinder were placed on the tomb of Archimedes at his request.

Archimedes (ca. 287 BCE – ca. 212 BCE), a colorful figure about whom many historical anecdotes are recorded, is remembered along with Euclid as one of the greatest of ancient mathematicians. Although the foundations of his work were put in place by Euclid, his work, unlike Euclid's, is believed to have been entirely his own original accomplishment. He proved equations for the volumes and areas of various figures in two and three dimensions, and enunciated the Archimedean property of finite numbers.

Apollonius of Perga (ca. 262 BCE–ca. 190 BCE) is mainly known for his investigation of conic sections.

René Descartes. Portrait after Frans Hals, 1648.

The 17th century: Descartes

René Descartes (1596-1650) developed analytic geometry, an alternative method for formalizing geometry. In this approach, a point is represented by its Cartesian (x, y) coordinates, a line is represented by its equation, and so on. In Euclid's original approach, the Pythagorean theorem follows from Euclid's axioms. In the Cartesian approach, the axioms are the axioms of algebra, and the equation expressing the Pythagorean theorem is then a definition of one of the terms in Euclid's axioms, which are now considered to be theorems. The equation

$|PQ|={\sqrt {(p-r)^{2}+(q-s)^{2}}}$

defining the distance between two points P = (p, q) and Q=(r, s) is then known as the Euclidean metric, and other metrics define non-Euclidean geometries.

In terms of analytic geometry, the restriction of classical geometry to compass and straightedge constructions means a restriction to first- and second-order equations, e.g., y = 2x + 1 (a line), or x² + y² = 7 (a circle).

Also in the 17th century, Girard Desargues, motivated by the theory of perspective, introduced the concept of idealized points, lines, and planes at infinity. The result can be considered as a type of generalized geometry, projective geometry, but it can also be used to produce proofs in ordinary Euclidean geometry in which the number of special cases is reduced.

Squaring the circle: the areas of this square and this circle are equal. In 1882, it was proven that this figure cannot be constructed in a finite number of steps with an idealized compass and straightedge.

The 18th century

Geometers of the 18th century struggled to define the boundaries of the Euclidean system. Many tried in vain to prove the fifth postulate from the first four. By 1763 at least 28 different proofs had been published, but all were found to be incorrect.

Leading up to this period, geometers also tried to determine what constructions could be accomplished in Euclidean geometry. For example, the problem of trisecting an angle with a compass and straightedge is one that naturally occurs within the theory, since the axioms refer to constructive operations that can be carried out with those tools. However, centuries of efforts failed to find a solution to this problem, until Pierre Wantzel published a proof in 1837 that such a construction was impossible. Other constructions that were proved to be impossible include doubling the cube and squaring the circle. In the case of doubling the cube, the impossibility of the construction originates from the fact that the compass and straightedge method involve first- and second-order equations, while doubling a cube requires the solution of a third-order equation.

Euler discussed a generalization of Euclidean geometry called affine geometry, which retains the fifth postulate unmodified while weakening postulates three and four in a way that eliminates the notions of angle (whence right triangles become meaningless) and of equality of length of line segments in general (whence circles become meaningless) while retaining the notions of parallelism as an equivalence relation between lines, and equality of length of parallel line segments (so line segments continue to have a midpoint).

The 19th century and non-Euclidean geometry

In the early 19th century, Carnot and Möbius systematically developed the use of signed angles and line segments as a way of simplifying and unifying results.

The century's most significant development in geometry occurred when, around 1830, János Bolyai and Nikolai Ivanovich Lobachevsky separately published work on non-Euclidean geometry, in which the parallel postulate is not valid. Since non-Euclidean geometry is provably self-consistent, the parallel postulate cannot be proved from the other postulates.

In the 19th century, it was also realized that Euclid's ten axioms and common notions do not suffice to prove all of theorems stated in the Elements. For example, Euclid assumed implicitly that any line contains at least two points, but this assumption cannot be proved from the other axioms, and therefore needs to be an axiom itself. The very first geometric proof in the Elements, shown in the figure above, is that any line segment is part of a triangle; Euclid constructs this in the usual way, by drawing circles around both endpoints and taking their intersection as the third vertex. His axioms, however, do not guarantee that the circles actually intersect, because they do not assert the geometrical property of continuity, which in Cartesian terms is equivalent to the completeness property of the real numbers. Starting with Moritz Pasch in 1882, many improved axiomatic systems for geometry have been proposed, the best known being those of Hilbert, George Birkhoff, and Tarski.

The 20th century and general relativity

A disproof of Euclidean geometry as a description of physical space. In a 1919 test of the general theory of relativity, stars (marked with short horizontal lines) were photographed during a solar eclipse. The rays of starlight were bent by the Sun's gravity on their way to the earth. This is interpreted as evidence in favor of Einstein's prediction that gravity would cause deviations from Euclidean geometry.

Einstein's theory of general relativity shows that the true geometry of spacetime is non-Euclidean geometry. For example, if a triangle is constructed out of three rays of light, then in general the interior angles do not add up to 180 degrees due to gravity. A relatively weak gravitational field, such as the Earth's or the sun's, is represented by a metric that is approximately, but not exactly, Euclidean. Until the 20th century, there was no technology capable of detecting the deviations from Euclidean geometry, but Einstein predicted that such deviations would exist. They were later verified by observations such as the observation of the slight bending of starlight by the Sun during a solar eclipse in 1919, and non-Euclidean geometry is now, for example, an integral part of the software that runs the GPS system. It is possible to object to the non-Euclidean interpretation of general relativity on the grounds that light rays might be improper physical models of Euclid's lines, or that relativity could be rephrased so as to avoid the geometrical interpretations. However, one of the consequences of Einstein's theory is that there is no possible physical test that can do any better than a beam of light as a model of geometry. Thus, the only logical possibilities are to accept non-Euclidean geometry as physically real, or to reject the entire notion of physical tests of the axioms of geometry, which can then be imagined as a formal system without any intrinsic real-world meaning.

Treatment of infinity

Infinite objects

Euclid sometimes distinguished explicitly between "finite lines" (e.g., Postulate 2) and "infinite lines" (book I, proposition 12). However, he typically did not make such distinctions unless they were necessary. The postulates do not explicitly refer to infinite lines, although for example some commentators interpret postulate 3, existence of a circle with any radius, as implying that space is infinite.

The notion of infinitesimally small quantities had previously been discussed extensively by the Eleatic School, but nobody had been able to put them on a firm logical basis, with paradoxes such as Zeno's paradox occurring that had not been resolved to universal satisfaction. Euclid used the method of exhaustion rather than infinitesimals.

Later ancient commentators such as Proclus (410-485 CE) treated many questions about infinity as issues demanding proof and, e.g., Proclus claimed to prove the infinite divisibility of a line, based on a proof by contradiction in which he considered the cases of even and odd numbers of points constituting it.

At the turn of the 20th century, Giuseppe Veronese produced controversial work on non-Archimedean models of Euclidean geometry, in which the distance between two points may be infinite or infinitesimal, in the Newton–Leibniz sense. Fifty years later, Abraham Robinson provided a rigorous logical foundation for Veronese's work.

Infinite processes

One reason that the ancients treated the parallel postulate as less certain than the others is that verifying it physically would require us to inspect two lines to check that they never intersected, even at some very distant point, and this inspection could potentially take an infinite amount of time.

The modern formulation of proof by induction was not developed until the 17th century, but some later commentators consider it to be implicit in some of Euclid's proofs, e.g., the proof of the infinitude of primes.

Supposed paradoxes involving infinite series, such as Zeno's paradox, predated Euclid. Euclid avoided such discussions, giving, for example, the expression for the partial sums of the geometric series in IX.35 without commenting on the possibility of letting the number of terms become infinite.

Logical basis

Main article: Real closed field

Euclid frequently used the method of proof by contradiction, and therefore the traditional presentation of Euclidean geometry assumes classical logic, in which every proposition is either true or false, i.e., for any proposition P, the proposition "P or not P" is automatically true.

Tarski (1902-1983) and his students demonstrated for the first time that Euclidean geometry can be expressed as a first-order theory. That is, it can be written entirely in a form that allows statements such as "for all points ...", without those like "for all sets of points ..." This is important because it shows that the subject does not depend on set theory for its logical basis. Tarski proved his axiomatic formulation of Euclidean geometry to be consistent and complete in a certain sense: there is an algorithm which, for every proposition, can show it to be either true or false. (This doesn't violate Gödel's theorem, because Euclidean geometry cannot describe a sufficient amount of arithmetic for the theorem to apply.) This is equivalent to the decidability of real closed fields, which Euclidean geometry is a model of.

See also

• Analytic geometry
• Interactive geometry software
• Non-Euclidean geometry
• Ordered geometry
• Incidence geometry
• Birkhoff's axioms
• Hilbert's axioms
• Tarski's axioms
• Parallel postulate
• Schopenhauer's criticism of the proofs of the Parallel Postulate
• Cartesian coordinate system

Classical theorems

• Ceva's theorem
• Heron's formula
• Nine-point circle
• Pythagorean theorem
• Tartaglia's formula
• Menelaus' theorem
• Angle bisector theorem
• Butterfly theorem

References

• Ball, W.W. Rouse (1960). A Short Account of the History of Mathematics (4th ed. [Reprint. Original publication: London: Macmillan & Co., 1908] ed.). New York: Dover Publications. pp. 50–62. ISBN 0-486-20630-0.
• Coxeter, H.S.M. (1961). Introduction to Geometry. New York: Wiley.
• Eves, Howard (1963). A Survey of Geometry. Allyn and Bacon.
• Franzén, Torkel (2005). Gödel's Theorem: An Incomplete Guide to its Use and Abuse. AK Peters. ISBN 1-56881-238-8.
• Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925] ed.). New York: Dover Publications. ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3). {{cite book}}: |format= requires |url= (help); Check |isbn= value: invalid character (help) Heath's authoritative translation of Euclid's Elements plus his extensive historical research and detailed commentary throughout the text.
• Hofstadter, Douglas R. (1979). Gödel, Escher, Bach: An Eternal Golden Braid. New York: Basic Books.
• Misner, Thorne, and Wheeler (1973). Gravitation. W.H. Freeman.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Mlodinow (2001). Euclid's Window. The Free Press.
• Nagel, E. and Newman, J.R. (1958). Gödel's Proof. New York University Press.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Alfred Tarski (1951) A Decision Method for Elementary Algebra and Geometry. Univ. of California Press.

External links

• Kiran Kedlaya, Geometry Unbound (a treatment using analytic geometry; PDF format, GFDL licensed)