Spirograph

Several Spirograph designs drawn with a Spirograph set.

Evolution of a typical Spirograph pattern.

Example of a Spirograph set

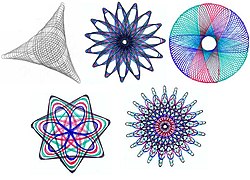
Spirograph is a geometric drawing toy that produces mathematical curves of the variety technically known as hypotrochoids and epitrochoids. The term has also been used to describe a variety of software applications that display similar curves, and applied to the class of curves that can be produced with the drawing equipment (so in this sense it may be regarded as a synonym of hypotrochoid). The name is a registered trademark of Hasbro, Inc.

History

The Spirograph was invented by the British engineer Denys Fisher, who exhibited it in 1965 at the Nuremberg International Toy Fair. It was subsequently produced by his company. Distribution rights were acquired by Kenner, Inc., which introduced it to the United States market in 1966.

Operation

A Spirograph consists of a set of plastic gears and other shapes such as rings, triangles, or straight bars. There are several sizes of gears and shapes, and all edges have teeth to engage any other piece. For instance, smaller gears fit inside the larger rings, but also can engage the outside of the rings in such a fashion that they rotate around the inside or along the outside edge of the rings.

To use it, a sheet of paper is placed on a heavy cardboard backing, and one of the plastic pieces—known as a stator—is pinned to the paper and cardboard. Another plastic piece—called the rotor—is placed so that its teeth engage with those of the pinned piece. For example, a ring may be pinned to the paper and a small gear placed inside the ring: the actual number of arrangements possible by combining different gears is very large. The point of a pen is placed in one of the holes of the rotor. As the rotor is moved, the pen traces out a curve.

The pen is used both to draw and to provide locomotive force; some practice is required before Spirograph can be operated without disengaging the stator and rotor. More intricate and unusual-shaped patterns may be made through the use of both hands, one to draw and one to guide the pieces. It is possible to move several pieces in relation to each other (say, the triangle around the ring, with a circle "climbing" from the ring onto the triangle), but this requires concentration or even additional assistance from other artists.

Mathematical Basis

Let us consider a fixed circle $C_{1}$ of radius $R$ centered at the origin. A smaller circle $C_{2}$ of radius $r<R$ is rolling inside $C_{1}$ and it is tangent to $C_{1}$. The inner circle cannot slip since teeth are present in a real Spirograph. Let us assume that a point $A$ that corresponds to hole in the inner circle of the Spirograph is located at the distance $\rho <r$ from the center of $C_{2}$. Without loss of generality we can assume that at the initial moment the point $A$ was on the $X$-axis. In order to find the trajectory created by a Spirograph we must follow $A$ as the inner circle is set in motion.

Let us mark two points $T$ on $C_{1}$ and $B$ on $C_{2}$. The point $T$ indicates where two circles are tangent all the time. Point $B$ however will travel on $C_{2}$ and its initial location coincides with $T$. After we set $C_{2}$ in motion counterclockwise, we will observe a clockwise rotation with respect to its center. The distances that point $B$ traverses on the the small circle is the same as the distance that the tangent point $T$ travels on the large circle due to absence of any slipping effects.

Let us consider the new (relative) system of coordinates $({\hat {X}},{\hat {Y}})$ with its origin at the center of $C_{2}$ and its axes parallel to $X$ and $Y$. If we define the parameter $t$ as the angle by which the tangent point $T$ rotates on $C_{1}$ and ${\hat {t}}$ is the angle by which $C_{2}$ rotates (i.e. by which $B$ travels) in the relative system of coordinates, then the distances traveled by $B$ and $T$ along their respective circles must be the same (no slipping). Thus we get

$tR=(t-{\hat {t}})r$

or equivalently

${\hat {t}}=-{\frac {R-r}{r}}t.$

It is common to assume that a counterclockwise motion results in a positive change of angle and a clockwise one will correspond to a negative change of angle. To accommodate this convention we introduced a minus sign in the formula above. (${\hat {t}}<0$)

Let $(x_{c},y_{c})$ be the coordinates of the center of $C_{2}$ in the absolute system of coordinates. Then $R-r$ represents the radius of the trajectory of the center of the inner circle, and

${\begin{array}{rcl}x_{c}&=&(R-r)\cos t,\\y_{c}&=&(R-r)\sin t.\end{array}}$

The coordinates of $A$ in the new system are $({\hat {x}},{\hat {y}})$ and they obey the regular law of circular motion (the angle of rotation in the relative system is ${\hat {t}}$):

${\begin{array}{rcl}{\hat {x}}&=&\rho \cos {\hat {t}},\\{\hat {y}}&=&\rho \sin {\hat {t}}.\end{array}}$

In order to obtain the trajectory of $A$ in the absolute (old) system of coordinates we add these two motions:

${\begin{array}{rcrcl}x&=&{\hat {x}}+x_{c}&=&(R-r)\cos t+\rho \cos {\hat {t}},\\y&=&{\hat {y}}+y_{c}&=&(R-r)\sin t+\rho \sin {\hat {t}},\\\end{array}}$

where $\rho$ is defined above.

Now we use the relation between $t$ and ${\hat {t}}$ as discussed above to obtain equations describing the trajectory of point $A$ in terms of one parameter $t$:

${\begin{array}{rcrcl}x&=&{\hat {x}}+x_{c}&=&(R-r)\cos t+\rho \cos {\frac {R-r}{r}}t,\\[4pt]y&=&{\hat {y}}+y_{c}&=&(R-r)\sin t-\rho \sin {\frac {R-r}{r}}t.\\\end{array}}$

(we used the fact that function $sin$ is odd)

It is convenient to represent the equation above in terms the radius $R$ of the largest circle and dimensionless parameters describing the structure of the Spirograph. Namely, let

$l={\frac {\rho }{r}}$

and

$k={\frac {r}{R}}.$

The parameter $0\leq l\leq 1$ represents how far the point $A$ is located from the center of the inner circle. At the same time, $0\leq k\leq 1$ represents how big the inner circle is with respect to the large one.

We observe that

${\frac {\rho }{R}}=lk,$

and therefore the trajectory equations take form of

${\begin{array}{rcl}x(t)&=&R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\[4pt]y(t)&=&R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{array}}$

Parameter $R$ is a scaling parameter and will not affect the structure of the Spirgoraph. It is interesting to note that two extreme cases of $k=0$ and $k=1$ will result in degenerate trajectories of the Spirograph. Namely when $k=1$ we will have a simple circle of radius $R$. And indeed this case corresponds to the case when the inner circle is shrunk into a point. (Division by $k=0$ in the formula is not a problem since both $\sin$ and $\cos$ are bounded functions).

The other extreme case $k=1$ corresponds to the inner circle matching the large circle. In this case the trajectory is a single point since the the inner circle is too large to roll without slipping.

If $l=1$ then we obtain the case when the point $A$ is on the circumference of the ineer circle. In this case the trajectories are called hypocycloids and the equations will match the one describing a hypocycloid.

See also

• Epicycloid
• Epitrochoid
• Guilloché
• Harmonograph
• Spirograph Nebula, a planetary nebula that displays delicate, spirograph-like filigree.
• Bruno Abakanowicz

External links

• Spirograph in Java
• Weisstein, Eric W. "Spirograph". MathWorld.
• Spirograph Toy Collection - Collection with photos of many versions including UK and Australian issues.
• Spirograph source files in C#
• Plotting Spirograph equations with gnuplot
• Ideas for spirographs in three dimensions
• An interactive Spirograph generator hosted by Google App-Engine