User:Earlster/Sandbox

Earlster/Sandbox

Example of insertion sort sorting a list of random numbers. Example of insertion sort sorting a list of random numbers.
Class	Sorting algorithm
Data structure	Array
Worst-case performance	$O(n)$
Best-case performance	$O(1)$
Average performance	$O(1.5)$
Worst-case space complexity	$O(n)$ total, $O(1)$

This is a WIP for Proxmap using the Bucket sort page as a template

Elements are distributed among bins

Then, elements are sorted within each bin

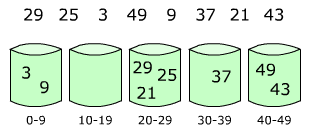
Proxmap Sort, or Proxmap, is a sorting algorithm that works by partitioning an array into a number of buckets. Several "tracking" arrays are used to reach what is known as the "proxmap," giving the sorting algorithm its title. A key is used to place each of the data into buckets using this proxmap. Data is dropped into each bucket and sorted individually by insertion sort. Since bucket sort is not a comparison sort, the Ω(n log n) lower bound is inapplicable. The computational complexity estimates involve the number of buckets and the key used.

ProxmapSort works as follows:

1. Set up an array of initially empty "buckets."
2. Assign an appropriate sorting key to match the data.
3. Scatter: Go over the original array, dropping each object into its bucket, insertion sorting as needed.
4. Gather: Visit the buckets in order and put all elements back into the original array.

Pseudocode

• Not yet implemented fully*

function proxmap-sort(array, n) is
  buckets ← new array of n empty lists
  for i = 0 to (length(array)-1) do
    insert array[i] into buckets[msbits(array[i], k)]
  for i = 0 to n - 1 do
    next-sort(buckets[i])
  return the concatenation of buckets[0], ..., buckets[n-1]

Here array is the array to be sorted and n is the number of buckets to use. The key function such as msbits(x,k) returns the k most significant bits of x (floor(x/2^(size(x)-k))); different functions can be used to translate the range of elements in array to n buckets, such as translating the letters A–Z to 0–25 or returning the first character (0–255) for sorting strings. Another method could simply take the floor of the incoming data divided by 10, or floor(k/10) Buckets get sorted as the data comes in, not all at the end.

Optimizations

Many optimizations include using the same array to store the sorted data, reusing the hitCount, proxMap, and location arrays used to sort the data. To be expanded on later...

Generic bucket sort

The most common variant of bucket sort operates on a list of n numeric inputs between zero and some maximum value M and divides the value range into n buckets each of size M/n. If each bucket is sorted using insertion sort, the sort can be shown to run in expected linear time (where the average is taken over all possible inputs). However, the performance of this sort degrades with clustering; if many values occur close together, they will all fall into a single bucket and be sorted slowly.

Comparison with other sorting algorithms

Generally, it works relatively fast when compared with other sorting algorithms as its not comparison-based. The function is nearly constant access time which makes it very appealing for large databases. Though it might take a few seconds to build, it saves thousands down the line. To be expanded on later...

References

• Thomas A. Standish "Using O(n) ProxmapSort and O(1) ProxmapSearch to Motivate CS2 Students (Part I)" from Donald Bren School of Information and Computer Sciences at UC Irvine.
• Norman Jacobson "A Synopsis of ProxmapSort & ProxmapSearch" from Donald Bren School of Information and Computer Sciences at UC Irvine.

External links

• http://www.cs.uah.edu/~rcoleman/CS221/Sorting/ProxMapSort.html