Jacobi elliptic functions

In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that are of historical importance. Many of their features show up in important structures and have direct relevance to some applications (e.g. the equation of a pendulum—also see pendulum (mathematics)). They also have useful analogies to the functions of trigonometry, as indicated by the matching notation sn for sin. The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi (1829).

Introduction

Auxiliary rectangle construction

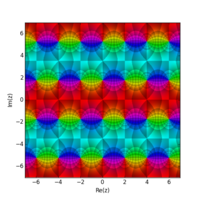
Jacobian elliptic functions are doubly periodic meromorphic functions on the complex plane. Since they are doubly periodic, they factor through a torus – in effect, their domain can be taken to be a torus, just as cosine and sine are in effect defined on a circle. Instead of having only one circle, we now have the product of two circles, one real and the other imaginary. The complex plane can be replaced by a complex torus. The circumference of the first circle is 4K and the second 4K′, where K and K′ are the quarter periods. Each function has two zeroes and two poles at opposite positions on the torus. Among the points 0, K, K + iK′, iK′ there is one zero and one pole. So an arrow can be drawn from a zero to a pole.

So there are twelve Jacobian elliptic functions. Each of the twelve corresponds to an arrow drawn from one corner of a rectangle to another. The corners of the rectangle are labeled, by convention, s, c, d and n. s is at the origin, c is at the point K on the real axis/loop, d is at the point K + iK′ and n is at point iK′ on the imaginary axis/loop. The twelve Jacobian elliptic functions are then pq, where each of p and q is a different one of the letters s, c, d, n.

The Jacobian elliptic functions are then the unique doubly periodic, meromorphic functions satisfying the following three properties:

• There is a simple zero at the corner p, and a simple pole at the corner q.
• The step from p to q is equal to half the period of the function pq u; that is, the function pq u is periodic in the direction pq, with the period being twice the distance from p to q. The function pq u is also periodic in the other two directions, with a period such that the distance from p to one of the other corners is a quarter period.
• If the function pq u is expanded in terms of u at one of the corners, the leading term in the expansion has a coefficient of 1. In other words, the leading term of the expansion of pq u at the corner p is u; the leading term of the expansion at the corner q is 1/u, and the leading term of an expansion at the other two corners is 1.

More generally, there is no need to impose a rectangle; a parallelogram will do. However, if K and iK' are kept on the real and imaginary axis respectively, then the Jacobi elliptic functions pq u will be real functions when u is real.

Jacobi elliptic function sn

Jacobi elliptic function cn

Jacobi elliptic function dn

Jacobi elliptic function sc

Images generated using a version of the domain coloring method.. All have values of the k parameter equal to 0.8.

Notation

The elliptic functions can be given in a variety of notations, which can make the subject unnecessarily confusing. Elliptic functions are functions of two variables. The first variable might be given in terms of the amplitude φ, or more commonly, in terms of u given below. The second variable might be given in terms of the parameter m, or as the elliptic modulus k, where k² = m, or in terms of the modular angle α, where m =  sin² α. A more extensive review and definition of these alternatives, their complements, and the associated notation schemes are given in the articles on elliptic integrals and quarter period.

The twelve Jacobi elliptic functions are generally written as pq(u,m) where ‘’p’’ and ‘’q’’ are any of the letters ‘’c’’, ‘’s’’, ‘’n’’, and ‘’d’’. Functions of the form pp(u,m) are trivially set to unity for notational completeness. The “major” functions are generally taken to be cn(u,m), sn(u,m) and dn(u,m) from which all other functions can be derived and expressions are often written solely in terms of these three functions, however, various symmetries and generalizations are often most conveniently expressed using the full set.

The functions are notationally related to each other by the multiplication rule: (arguments suppressed)

$\operatorname {pq} \,\,\,\,\operatorname {p'q'} =\operatorname {pq'} \,\,\,\operatorname {p'q}$

from which other commonly used relationships can be derived:

$\operatorname {pr} /\operatorname {qr} =\operatorname {pq}$

$1/\operatorname {qp} =\operatorname {pq}$

Definition as inverses of elliptic integrals

Model of amplitude (measured along vertical axis) as a function of independent variables u and k

The above definition, in terms of the unique meromorphic functions satisfying certain properties, is quite abstract. There is a simpler, but completely equivalent definition, giving the elliptic functions as inverses of the incomplete elliptic integral of the first kind. Let

$u=\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1-m\sin ^{2}\theta }}}\,.$

Then the elliptic sine sn u (Latin: sinus amplitudinis) is given by

$\operatorname {sn} u=\sin \varphi \,$

and the elliptic cosine cn u (Latin: cosinus amplitudinis) is given by

$\operatorname {cn} u=\cos \varphi$

and the delta amplitude dn u (Latin: delta amplitudinis)

$\operatorname {dn} u={\sqrt {1-m\sin ^{2}\varphi }}\,.$

Here, the angle $\varphi$ is called the amplitude. On occasion, dn u = Δ(u) is called the delta amplitude. In the above, the value m is a free parameter, usually taken to be real, 0 ≤ m ≤ 1, and so the elliptic functions can be thought of as being given by two variables, the amplitude $\varphi$ and the parameter m.

The remaining nine elliptic functions are easily built from the above three, and are given in a section below.

Note that when $\varphi =\pi /2$, that u then equals the quarter period K.

Definition as trigonometry

Plot of the Jacobi ellipse (x²+y²/b²=1, b real) and the twelve Jacobi Elliptic functions pq(u,m) for particular values of angle φ and parameter b. The solid curve is the ellipse, with m=1-1/b² and u=F(φ,m) where F(.,.) is the elliptic integral of the first kind. The dotted curve is the unit circle. For the ds-dc triangle,σ= Sin(φ)Cos(φ).

$\cos \varphi ,\sin \varphi$ are defined on the unit circle, with radius r = 1 and angle $\varphi =$ arc length of the unit circle measured from the positive x-axis. Similarly, Jacobi elliptic functions are defined on the unit ellipse, with a = 1. Let

${\begin{aligned}&x^{2}+{\frac {y^{2}}{b^{2}}}=1,\quad b>1,\\&m=1-{\frac {1}{b^{2}}},\quad 0<m<1,\\&x=r\cos \varphi ,\quad y=r\sin \varphi \end{aligned}}$

then:

$r(\varphi ,m)={\frac {1}{\sqrt {1-m\sin ^{2}\varphi }}}\,.$

For each angle $\varphi$ the angular component of the arc length, the 'angular arc length' is computed. An advantage of angular arc length is that we can calculate a total arc length for hyperbolas. Force $\times$ angular arc length, is the energy required to turn a lever with constant force. For the ellipse the angular arc length is:

$u=u(\varphi ,m)=\int _{0}^{\varphi }r(\theta ,m)\,d\theta .$

Let $P=(x,y)$ be the point on the ellipse with angular arc length $u(\varphi ,m)$ and let $P'=(x',y')$ be the point on the unit circle with the angular arc length $\varphi$, (note that origin $O,P'$ and $P$ are on the same straight line). The familiar relations from the unit circle ($OP'=1$):

$x'=\cos \varphi ,\quad y'=\sin \varphi$

imply for the ellipse:

$x'=\operatorname {cn} (u,m),\quad y'=\operatorname {sn} (u,m).$

So the projections of the intersection point $P'$ of the line $OP$ with the unit circle on the x- and y-axes are simply $\operatorname {cn} (u,m)$ and $\operatorname {sn} (u,m)$. These projections may be interpreted as 'definition as trigonometry'. In short:

$\operatorname {cn} (u,m)={\frac {x(u,m)}{r(u,m)}},\quad \operatorname {sn} (u,m)={\frac {y(u,m)}{r(u,m)}},\quad \operatorname {dn} (u,m)={\frac {1}{r(u,m)}}.$

For the $x$ and $y$ value of the point $P$ with $u$ and parameter $m$ we get, after inserting the relation:

$r(\varphi ,m)={\frac {1}{\operatorname {dn} (u,m)}}$

into:$x=r(\varphi ,m)\cos(\varphi ),y=r(\varphi ,m)\sin(\varphi )$ that:

$x={\frac {\operatorname {cn} (u,m)}{\operatorname {dn} (u,m)}},\quad y={\frac {\operatorname {sn} (u,m)}{\operatorname {dn} (u,m)}}.$

The latter relations for the x- and y-coordinates of points on the unit ellipse may be considered as generalization of the relations $x=\cos \varphi ,y=\sin \varphi$ for the coordinates of points on the unit circle.

The following table summarizes the expressions for all Jacobi elliptic functions pq(u,m) in the variables (x,y) and (φ,dn);

Jacobi Elliptic Functions pq[u,m] as functions of {x,y} and {φ,dn}

		q
		c	s	n	d
p
	c	1	$x/y=\cot(\phi )$	$x/r=\cos(\phi )$	$x=\cos(\phi )/dn$
	s	$y/x=\tan(\phi )$	1	$y/r=\sin(\phi )$	$y=\sin(\phi )/dn$
	n	$r/x=\sec(\phi )$	$r/y=\csc(\phi )$	1	$r=1/dn$
	d	$1/x=dn\sec(\phi )$	$1/y=dn\csc(\phi )$	$1/r=dn$	1

The Jacobi imaginary transformations

Plot of the degenerate Jacobi curve (x²+y²/b²=1, b=infinity) and the twelve Jacobi Elliptic functions pq(u,1) for a particular value of angle φ. The solid curve is the degenerate ellipse (x²=1) with m=1 and u=F(φ,1) where F(.,.) is the elliptic integral of the first kind.. The dotted curve is the unit circle. Since these are the Jacobi functions for m=0 (circular trigonometric functions) but with imaginary arguments, they correspond to the six hyperbolic trigonometric functions.

The Jacobi imaginary transformations relate various functions of the imaginary variable i u or, equivalently, relations between various values of the m parameter:

$\operatorname {cn} (iu,m)=\operatorname {nc} (u,1-m)$

$\operatorname {sn} (iu,m)=i\operatorname {sc} (u,1-m)$

$\operatorname {dn} (iu,m)=\operatorname {dc} (u,1-m)$

Using the multiplication rule all other derivatives may be expressed in terms of the above three. The following table gives pq'(u,1-m) for the given pq(iu,m) (arguments (u,m-1) supressed)

Jacobi Imaginary transformations pq(iu,m)=pq'(u,1-m)

		q
		c	s	n	d
p
	c	1	- i ns	nc	nd
	s	i sn	1	i sc	i sd
	n	cn	-i cs	1	cd
	d	dn	-i ds	dc	1

Since the hyperbolic trigonometric functions are proportional to the circular trigonometric functions with imaginary arguments, it follows that the Jacobi functions will yield the hyperbolic functions for m=1. In the figure, the Jacobi curve has degenerated to two vertical lines at x=1 and x=-1.

The dual - Jacobi unit hyperbola

Plot of the Jacobi hyperbola (x²+y²/b²=1, b imaginary) and the twelve Jacobi Elliptic functions pq(u,m) for particular values of angle φ and parameter b. The solid curve is the hyperbola, with m=1-1/b² and u=F(φ,m) where F(.,.) is the elliptic integral of the first kind. The dotted curve is the unit circle. For the ds-dc triangle,σ= Sin(φ)Cos(φ).

Introducing complex numbers, our ellipse has a dual hyperbola:

$xx^{2}-{\frac {yy^{2}}{b^{2}}}=1$

from applying Jacobi's imaginary transformation to the elliptic functions in the above equation for x and y.

$xx={\frac {1}{\operatorname {dn} (u,1-m)}},\quad yy={\frac {\operatorname {sn} (u,1-m)}{\operatorname {dn} (u,1-m)}}$

It follows that we can put $x=\operatorname {dn} (u,1-m),y=\operatorname {sn} (u,1-m)$. So our ellipse also has a dual ellipse with m replaced by 1-m.

Definition in terms of theta functions

Equivalently, Jacobi's elliptic functions can be defined in terms of his theta functions. If we abbreviate $\vartheta (0;\tau )$ as $\vartheta$, and $\vartheta _{01}(0;\tau ),\vartheta _{10}(0;\tau ),\vartheta _{11}(0;\tau )$ respectively as $\vartheta _{01},\vartheta _{10},\vartheta _{11}$ (the theta constants) then the elliptic modulus k is $k=\left({\vartheta _{10} \over \vartheta }\right)^{2}$. If we set $u=\pi \vartheta ^{2}z$, we have

${\begin{aligned}\operatorname {sn} (u;k)&=-{\vartheta \vartheta _{11}(z;\tau ) \over \vartheta _{10}\vartheta _{01}(z;\tau )}\\[7pt]\operatorname {cn} (u;k)&={\vartheta _{01}\vartheta _{10}(z;\tau ) \over \vartheta _{10}\vartheta _{01}(z;\tau )}\\[7pt]\operatorname {dn} (u;k)&={\vartheta _{01}\vartheta (z;\tau ) \over \vartheta \vartheta _{01}(z;\tau )}\end{aligned}}$

Since the Jacobi functions are defined in terms of the elliptic modulus k(τ), we need to invert this and find τ in terms of k. We start from $k'={\sqrt {1-k^{2}}}$, the complementary modulus. As a function of τ it is

$k'(\tau )=\left({\vartheta _{01} \over \vartheta }\right)^{2}.$

Let us first define

$\ell ={1 \over 2}{1-{\sqrt {k'}} \over 1+{\sqrt {k'}}}={1 \over 2}{\vartheta -\vartheta _{01} \over \vartheta +\vartheta _{01}}.$

Then define the nome q as $q=\exp(\pi i\tau )$ and expand $\ell$ as a power series in the nome q, we obtain

$\ell ={q+q^{9}+q^{25}+\cdots \over 1+2q^{4}+2q^{16}+\cdots }.$

Reversion of series now gives

$q=\ell +2\ell ^{5}+15\ell ^{9}+150\ell ^{13}+1707\ell ^{17}+20910\ell ^{21}+268616\ell ^{25}+\cdots .$

Since we may reduce to the case where the imaginary part of τ is greater than or equal to 1/2 sqrt(3), we can assume the absolute value of q is less than or equal to exp(-1/2 sqrt(3) π) ~ 0.0658; for values this small the above series converges very rapidly and easily allows us to find the appropriate value for q.

Minor functions

Reversing the order of the two letters of the function name results in the reciprocals of the three functions above:

${\begin{aligned}\operatorname {ns} (u)={\frac {1}{\operatorname {sn} (u)}},\qquad \operatorname {nc} (u)={\frac {1}{\operatorname {cn} (u)}},\qquad \operatorname {nd} (u)={\frac {1}{\operatorname {dn} (u)}}.\end{aligned}}$

Similarly, the ratios of the three primary functions correspond to the first letter of the numerator followed by the first letter of the denominator:

${\begin{aligned}\operatorname {sc} (u)={\frac {\operatorname {sn} (u)}{\operatorname {cn} (u)}},\qquad \operatorname {sd} (u)={\frac {\operatorname {sn} (u)}{\operatorname {dn} (u)}},\qquad \operatorname {dc} (u)={\frac {\operatorname {dn} (u)}{\operatorname {cn} (u)}},\qquad \operatorname {ds} (u)={\frac {\operatorname {dn} (u)}{\operatorname {sn} (u)}},\qquad \operatorname {cs} (u)={\frac {\operatorname {cn} (u)}{\operatorname {sn} (u)}},\qquad \operatorname {cd} (u),={\frac {\operatorname {cn} (u)}{\operatorname {dn} (u)}}.\end{aligned}}$

More compactly, we have

$\operatorname {pq} (u)={\frac {\operatorname {pn} (u)}{\operatorname {qn} (u)}}$

where p and q are any of the letters s, c, d.

(This notation is due to Gudermann and Glaisher and is not Jacobi's original notation)

Relations between squares of the functions

Relations between squares of the functions can be derived from two basic relationships (Arguments (u,m) suppressed):

$\operatorname {cn} ^{2}+\operatorname {sn} ^{2}=1$

$\operatorname {cn} ^{2}+m_{1}\operatorname {sn} ^{2}=\operatorname {dn} ^{2}$

where m + m₁ = 1 and m = k². Multiplying by any function of the form nq yields more general equations:

$\operatorname {cq} ^{2}+\operatorname {sq} ^{2}=\operatorname {nq} ^{2}$

$\operatorname {cq} ^{2}+m_{1}\operatorname {sq} ^{2}=\operatorname {dq} ^{2}$

With q=d, these correspond trigonometrically to the equations for the unit circle ($x^{2}+y^{2}=r^{2}$) and the unit ellipse ($x^{2}+m_{1}y^{2}=1$), with x=cd, y=sd and r=nd. Using the multiplication rule, other relationships may be derived. For example:

$-\operatorname {dn} ^{2}+m_{1}=-m\operatorname {cn} ^{2}=m\operatorname {sn} ^{2}-m$

$-m_{1}\operatorname {nd} ^{2}+m_{1}=-mm_{1}\operatorname {sd} ^{2}=m\operatorname {cd} ^{2}-m$

$m_{1}\operatorname {sc} ^{2}+m_{1}=m_{1}\operatorname {nc} ^{2}=\operatorname {dc} ^{2}-m$

$\operatorname {cs} ^{2}+m_{1}=\operatorname {ds} ^{2}=\operatorname {ns} ^{2}-m$

Addition theorems

The functions satisfy the two square relations

$\operatorname {cn} ^{2}(u,k)+\operatorname {sn} ^{2}(u,k)=1,\,$

$\operatorname {dn} ^{2}(u,k)+k^{2}\operatorname {sn} ^{2}(u,k)=1.\,$

From this we see that (cn, sn, dn) parametrizes an elliptic curve which is the intersection of the two quadrics defined by the above two equations. We now may define a group law for points on this curve by the addition formulas for the Jacobi functions

${\begin{aligned}\operatorname {cn} (x+y)&={\operatorname {cn} (x)\operatorname {cn} (y)-\operatorname {sn} (x)\operatorname {sn} (y)\operatorname {dn} (x)\operatorname {dn} (y) \over {1-k^{2}\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {sn} (x+y)&={\operatorname {sn} (x)\operatorname {cn} (y)\operatorname {dn} (y)+\operatorname {sn} (y)\operatorname {cn} (x)\operatorname {dn} (x) \over {1-k^{2}\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {dn} (x+y)&={\operatorname {dn} (x)\operatorname {dn} (y)-k^{2}\operatorname {sn} (x)\operatorname {sn} (y)\operatorname {cn} (x)\operatorname {cn} (y) \over {1-k^{2}\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}}.\end{aligned}}$

Expansion in terms of the nome

Let the nome be $q=\exp(-\pi K'/K)$ and let the argument be $v=\pi u/(2K)$. Then the functions have expansions as Lambert series

$\operatorname {sn} (u)={\frac {2\pi }{K{\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1-q^{2n+1}}}\sin((2n+1)v),$

$\operatorname {cn} (u)={\frac {2\pi }{K{\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1+q^{2n+1}}}\cos((2n+1)v),$

$\operatorname {dn} (u)={\frac {\pi }{2K}}+{\frac {2\pi }{K}}\sum _{n=1}^{\infty }{\frac {q^{n}}{1+q^{2n}}}\cos(2nv).$

Jacobi elliptic functions as solutions of nonlinear ordinary differential equations

The derivatives of the three basic Jacobi elliptic functions are:

${\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sn} (z)=\operatorname {cn} (z)\operatorname {dn} (z),$

${\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cn} (z)=-\operatorname {sn} (z)\operatorname {dn} (z),$

${\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {dn} (z)=-k^{2}\operatorname {sn} (z)\operatorname {cn} (z).$

These can be used to derive the derivatives of all other functions as shown in the table below (arguments (u,m) suppressed):

Derivatives ${\frac {d}{du}}\operatorname {pq} (u,m)$

		q
		c	s	n	d
p
	c	0	-ds ns	-dn sn	-m1 nd sd
	s	dc nc	0	cn dn	cd nd
	n	dc sc	-cs ds	0	m cd sd
	d	m1 nc sc	-cs ns	-m cn sn	0

With the addition theorems above and for a given k with 0 < k < 1 the major functions are therefore are solutions to the following nonlinear ordinary differential equations:

• $\operatorname {sn} (x)$ solves the differential equations

${\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1+k^{2})y-2k^{2}y^{3}=0$

and

$\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}y^{2})$

• $\operatorname {cn} (x)$ solves the differential equations

${\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1-2k^{2})y+2k^{2}y^{3}=0$

and

$\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}+k^{2}y^{2})$

• $\operatorname {dn} (x)$ solves the differential equations

${\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}-(2-k^{2})y+2y^{3}=0$

and

$\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(y^{2}-1)(1-k^{2}-y^{2})$

Approximation in terms of hyperbolic functions

The Jacobi elliptic functions can be expanded in terms of the hyperbolic functions. When $m$ is close to unity, such that $m_{1}^{2}$ and higher power of $m_{1}$ can be neglected, we have

• sn(u):

$\operatorname {sn} (u,m)\approx \tanh(u)+{\frac {1}{4}}m_{1}(\sinh(u)\cosh(u)-u)\operatorname {sech} ^{2}(u).$

• cn(u):

$\operatorname {cn} (u,m)\approx \operatorname {sech} (u)-{\frac {1}{4}}m_{1}(\sinh(u)\cosh(u)-u)\tanh u\operatorname {sech} (u).$

• dn(u):

$\operatorname {dn} (u,m)\approx \operatorname {sech} (u)+{\frac {1}{4}}m_{1}(\sinh(u)\cosh(u)+u)\tanh(u)\operatorname {sech} (u).$

• am(u):

$\operatorname {am} (u,m)\approx \operatorname {gd} (u)+{\frac {1}{4}}m_{1}(\sinh(u)\cosh(u)-u)\operatorname {sech} (u).$

Inverse functions

The inverses of the Jacobi elliptic functions can be defined similarly to the inverse trigonometric functions; if $x=\operatorname {sn} (\xi ,k)$, $\xi =\mathrm {arcsn} (x,k)$. They can be represented as elliptic integrals, and power series representations have been found.

• $\mathrm {arcsn} \,(x,k)=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(1-k^{2}t^{2})}}}$
• $\mathrm {arccn} \,(x,k)=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(1-k^{2}+k^{2}t^{2})}}}$
• $\mathrm {arcdn} \,(x,k)=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})(t^{2}+k^{2}-1)}}}$

Map projection

The Peirce quincuncial projection is a map projection based on Jacobian elliptic functions.

See also

• Elliptic integral
• Elliptic curve
• Schwarz–Christoffel mapping
• Carlson symmetric form
• Jacobi theta function
• Ramanujan theta function
• Dixon elliptic functions
• Abel elliptic functions
• Weierstrass's elliptic functions

References

• Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 16". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 569. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
• N. I. Akhiezer, Elements of the Theory of Elliptic Functions, (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
• A. C. Dixon The elementary properties of the elliptic functions, with examples (Macmillan, 1894)
• Alfred George Greenhill The applications of elliptic functions (London, New York, Macmillan, 1892)
• H. Hancock Lectures on the theory of elliptic functions (New York, J. Wiley & sons, 1910)
• Jacobi, C. G. J. (1829), Fundamenta nova theoriae functionum ellipticarum (in Latin), Königsberg, ISBN 978-1-108-05200-9, Reprinted by Cambridge University Press 2012
• Reinhardt, William P.; Walker, Peter L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
• E. T. Whittaker and G. N. Watson A Course of Modern Analysis, (1940, 1996) Cambridge University Press. ISBN 0-521-58807-3
• Template:Fr icon P. Appell and E. Lacour Principes de la théorie des fonctions elliptiques et applications (Paris, Gauthier Villars, 1897)
• Template:Fr icon G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 1) (Paris, Gauthier-Villars, 1886–1891)
• Template:Fr icon G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 2) (Paris, Gauthier-Villars, 1886–1891)
• Template:Fr icon G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 3) (Paris, Gauthier-Villars, 1886–1891)
• Template:Fr icon J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome I, Introduction. Calcul différentiel. Ire partie (Paris : Gauthier-Villars et fils, 1893)
• Template:Fr icon J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome II, Calcul différentiel. IIe partie (Paris : Gauthier-Villars et fils, 1893)
• Template:Fr icon J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome III, Calcul intégral. Ire partie, Théorèmes généraux. Inversion (Paris : Gauthier-Villars et fils, 1893)
• Template:Fr icon J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome IV, Calcul intégral. IIe partie, Applications (Paris : Gauthier-Villars et fils, 1893)
• Template:Fr icon C. Briot and J. C. Bouquet Théorie des fonctions elliptiques ( Paris : Gauthier-Villars, 1875)

External links

• "Jacobi elliptic functions", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Jacobi Elliptic Functions". MathWorld.