Logit
In mathematics, especially as applied in statistics, the logit (pronounced with a long "o" and a soft "g", IPA /loʊdʒɪt/) of a number p between 0 and 1 is
This function is used in logistic regression.
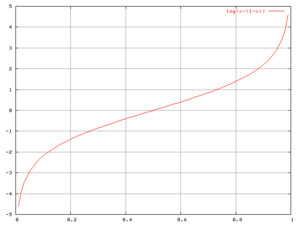
(The base of the logarithm function used here is of little importance in the present article, as long as it is greater than 1.) The logit function is the inverse of the "sigmoid", or "logistic" function. If p is a probability then p/(1 − p) is the corresponding odds, and the logit of the probability is the logarithm of the odds; similarly the difference between the logits of two probabilities is the logarithm of the odds-ratio, thus providing an additive mechanism for combining odds-ratios.
Logits are used for various purposes by statisticians. In particular there is the "logit model" of which the simplest sort is
where xi is some quantity on which success or failure in the i-th in a sequence of Bernoulli trials may depend, and pi is the probability of success in the i-th case. For example, x may be the age of a patient admitted to a hospital with a heart attack, and "success" may be the event that the patient dies before leaving the hospital. Having observed the values of x in a sequence of cases and whether there was a "success" or a "failure" in each such case, a statistician will often estimate the values of the coefficients a and b by the method of maximum likelihood. The result can then be used to assess the probability of "success" in a subsequent case in which the value of x is known. Estimation and prediction by this method are called logistic regression.
A logistic regression model can be seen as a feedforward neural network with no hidden units.
The logit in logistic regression is a special case of a link function in generalized linear models. Another example is the probit model, which differs from the logit by a constant factor except in the tails.
The concept of a logit is also central to the probabilistic Rasch model for measurement, which has applications in psychological and educational assessment, among other areas.
The logit model was introduced by Joseph Berkson in 1944, who coined the term. The term was borrowed by analogy from the very similar probit model developed by C.I. Bliss in 1934. G. A. Barnard in 1949 coined the commonly used term log-odds; the log-odds of an event is the logit of the probability of the event.
See also
- Daniel McFadden, winner of the Bank of Sweden Prize in Economic Sciences in Memory of Alfred Nobel for development of a particular logit model used in economics
- Logistic function
- Logit analysis in marketing
- Perceptron


