Girth (graph theory): Difference between revisions
m Bot: Migrating langlinks to WP:Wikidata - d:q959831 |
→Cages: The dashes were misleading, creating the impression that they provided some explanation, when in fact what given between them is part of the definition! |
||
| Line 3: | Line 3: | ||
==Cages== |
==Cages== |
||
A [[cubic graph]] (all vertices have degree three) of girth {{math|''g''}} |
A [[cubic graph]] (all vertices have degree three) of girth {{math|''g''}} that is as small as possible is known as a {{math|''g''}}-[[cage (graph theory)|cage]] (or as a (3,{{math|''g''}})-cage). The [[Petersen graph]] is the unique 5-cage (it is the smallest cubic graph of girth 5), the [[Heawood graph]] is the unique 6-cage, the [[McGee graph]] is the unique 7-cage and the [[Tutte eight cage]] is the unique 8-cage.<ref>{{citation|first=Andries E.|last=Brouwer|authorlink=Andries Brouwer|url=http://www.win.tue.nl/~aeb/drg/graphs/|title=Cages}}. Electronic supplement to the book ''Distance-Regular Graphs'' (Brouwer, Cohen, and Neumaier 1989, Springer-Verlag).</ref> There may exist multiple cages for a given girth. For instance there are three nonisomorphic 10-cages, each with 70 vertices : the [[Balaban 10-cage]], the [[Harries graph]] and the [[Harries-Wong graph]]. |
||
<gallery> |
<gallery> |
||
Revision as of 06:19, 30 March 2013
In graph theory, the girth of a graph is the length of a shortest cycle contained in the graph.[1] If the graph does not contain any cycles (i.e. it's an acyclic graph), its girth is defined to be infinity.[2] For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.
Cages
A cubic graph (all vertices have degree three) of girth g that is as small as possible is known as a g-cage (or as a (3,g)-cage). The Petersen graph is the unique 5-cage (it is the smallest cubic graph of girth 5), the Heawood graph is the unique 6-cage, the McGee graph is the unique 7-cage and the Tutte eight cage is the unique 8-cage.[3] There may exist multiple cages for a given girth. For instance there are three nonisomorphic 10-cages, each with 70 vertices : the Balaban 10-cage, the Harries graph and the Harries-Wong graph.
-
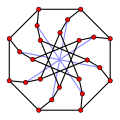
The Petersen graph has a girth of 5
-
The Heawood graph has a girth of 6
-
The McGee graph has a girth of 7
-
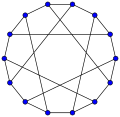
The Tutte–Coxeter graph (Tutte eight cage) has a girth of 8
Girth and graph coloring
For any positive integers g and χ, there exists a graph with girth at least g and chromatic number at least χ; for instance, the Grötzsch graph is triangle-free and has chromatic number 4, and repeating the Mycielskian construction used to form the Grötzsch graph produces triangle-free graphs of arbitrarily large chromatic number. Paul Erdős was the first to prove the general result, using the probabilistic method.[4] More precisely, he showed that a random graph on n vertices, formed by choosing independently whether to include each edge with probability n(1 − g)/g, has, with probability tending to 1 as n goes to infinity, at most n/2 cycles of length g or less, but has no independent set of size n/2k. Therefore, removing one vertex from each short cycle leaves a smaller graph with girth greater than g, in which each color class of a coloring must be small and which therefore requires at least k colors in any coloring.
Related concepts
The odd girth and even girth of a graph are the lengths of a shortest odd cycle and shortest even cycle respectively.
Thought of as the least length of a non-trivial cycle, the girth admits natural generalisations as the 1-systole or higher systoles in systolic geometry.
References
- ^ R. Diestel, Graph Theory, p.8. 3rd Edition, Springer-Verlag, 2005
- ^ Girth -- Wolfram MathWorld
- ^ Brouwer, Andries E., Cages. Electronic supplement to the book Distance-Regular Graphs (Brouwer, Cohen, and Neumaier 1989, Springer-Verlag).
- ^ Erdős, Paul (1959), "Graph theory and probability", Canadian Journal of Mathematics, 11: 34–38, doi:10.4153/CJM-1959-003-9.