User:Shapeyness/sandbox/Explanatory indispensability argument

From Wikipedia, the free encyclopedia
< User:Shapeyness‎ | sandbox

This is an old revision of this page, as edited by Shapeyness (talk | contribs) at 20:17, 28 April 2024 (→‎Others). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

The explanatory indispensability argument[a] is an altered form of the Quine–Putnam indispensability argument in the philosophy of mathematics. It claims that we should believe in mathematical objects such as numbers because they are indispensable to scientific explanations of empirical phenomena.

Origin

The explanatory indispensability argument is an example of an indispensability argument, which is an argument in which the conclusion is supported by the claim that its truth is indispensable or necessary for a certain purpose.[3] In particular, it is an altered form of the Quine–Putnam indispensability argument[4] first raised by W. V. Quine and Hilary Putnam in the 1960s and 1970s.[5] The Quine–Putnam indispensability argument supports the conclusion that mathematical objects exist with the idea that mathematics is indispensable to our best scientific theories.[6] It relies on the view, called confirmational holism, that scientific theories are confirmed as wholes, and that the confirmations of science extend to the mathematics it makes use of.[7]

The reliance of the Quine–Putnam argument on confirmational holism is controversial, and it has faced influential challenges from Penelope Maddy and Elliott Sober.[8] The argument has also been criticized for failing to specify the way in which mathematics is indispensable to science; according to Joseph Melia, we only need to believe in mathematics if it is indispensable in the right way.[9] Specifically, it needs to be indispensable to scientific explanations for it to be as strongly justified as theoretical entities such as electrons.[10] This claim by Melia arose through a debate with Mark Colyvan in the early 2000s over the argument, with Colyvan claiming that mathematics enhances the explanatory power of science. Inspired by this debate, Alan Baker (2005, 2009) developed an explicitly explanatory form of the indispensability argument, which he termed the enhanced indispensability argument.[11] He was also motivated by the objections against confirmational holism; his formulation aimed to replace confirmational holism with an inference to the best explanation.[12]

Among Baker's influences was Hartry Field, who had previously been the first person to draw a connection between indispensability arguments and explanation.[13] Baker cited Field as originating an explanatory form of the argument,[14] although Sorin Bangu states that Field merely alluded to such an argument without fully developing it,[15] and Russell Marcus argues he was discussing explanation within the context of the original Quine–Putnam indispensability argument rather than suggesting a new explanatory indispensability argument.[16] According to Marcus, Colyvan's discussion of explanatory power was also initially on its role within the Quine–Putnam indispensability argument, with the explanatory indispensability argument originating with Baker.[17] Others credit Colyvan and Baker equally with the origination of the argument. [cite this, also maybe specify who says this]


(The Stanford Encyclopedia of Philosophy credits the argument to Baker[18] while the Internet Encyclopedia of Philosophy credits it to both Colyvan and Baker.[19])

Important precursors to the argument are Mark Steiner (1978a, 1978b) and J. J. C. Smart (1990) for their work on mathematical explanation.[20] [maybe cut this]

[Busch & Sereni argue that it is fundamentally different to the QPIA argument and cannot be considered Quinean - maybe include? as an explanatory footnote after part about IBE?]

Overview

A standard formulation of the explanatory indispensability argument is given as follows:[21]

  • We ought rationally to believe in the existence of any entity which plays an indispensable explanatory role in our best scientific theories.
  • Mathematical objects play an indispensable explanatory role in science.
  • Therefore, we ought rationally to believe in the existence of mathematical objects.

Talk about assumptions: parity premise and existence premise

Genuinely mathematical explanations are not just explanations that are expressed with the help of mathematics, mathematics has to be doing the explanatory work (Wójtowicz 2020 p. 184, Târziu p. 394, see also Bangu p. 152) - maybe this needs its own section

Also talk about role of case studies in the argument (Paseau & Baker §3.5, Bangu p. 152, Baker 2021 p. 157)

Explain / discuss IBE

Maybe talk about target of argument (scientific realists) and motivation from epistemological problem

Case studies

Periodical cicadas

Number line with multiples of 3 and 4 highlighted up to the number 12. An illustration of a cicada sits at the number 13.
Number line visualizing why prime-numbered life cycles are advantageous compared to non-prime life cycles. If predators have life cycles of 3 or 4 years, they quickly synchronize with a non-prime life cycle such as a life cycle of 12 years. But they will not synchronize with a 13-year periodical cicada's life cycle until 39 and 52 years have passed, respectively.

The most influential case study is the example of periodical cicadas provided by Baker.[22] Periodical cicadas are a type of insect that usually have life cycles of 13 or 17 years. It is hypothesized that this is an evolutionary advantage because 13 and 17 are prime numbers. Because prime numbers have no non-trivial factors, this means it is less likely that periodic predators and other competing species of cicada can synchronize with periodic cicadas' life cycles.[23] Baker argues that this is an explanation in which mathematics, specifically number theory, plays a key role in explaining an empirical phenomenon.[24]

A number of non-mathematical explanations have been proposed for the length of periodical cicadas' life cycles. For example, a prominent alternative explanation claims that prime-numbered life cycles could have emerged from non-prime life cycles due to developmental delays. This hypothesis is supported by the fact that there are many other species of cicada that have non-prime life cycles, and that developmental changes with 4-year periods have often been observed in periodical cicadas.[25] Some philosophers have also argued that the concept of primeness in the case study by Baker can be replaced with a non-numeric concept of "intersection-minimizing periods", although Baker has argued that this would reduce the generality and depth of the explanation.[26]

The case study has also been criticized for assuming that periodical cicadas have had predators with periodic life cycles in their evolutionary history.[27] Baker has responded to this worry by arguing that it would be impossible to provide direct evidence that periodical cicadas have had periodic predators because "periodicity is not something that can be gleaned from the fossil record".[28] However, he has attempted to make the claim more plausible by arguing for the possibility of ecological constraints that would have restricted the range of the cicadas' possible life cycles, lessening the requirements on periodic predators for the case study to remain mathematically sound.[29]

[perhaps some coverage of arbitrariness of measuring life cycles in years instead of e.g. months / seasons + Baker's responses]

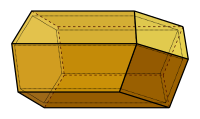
Bee honeycomb

A bee on some honeycomb
Hexagonal structure of bee honeycomb
A diagram showing the 3D structure of a honeycomb cell
3D structure of a honeycomb cell, with hexagonal opening on the left-hand side

Another prominent case study suggested by Aidan Lyon and Colyvan is the hexagonal structure of bee honeycomb. Lyon and Colyvan contend that the hexagonal structure of bee honeycomb can be explained by the mathematical proof of the honeycomb conjecture, which states that hexagons are the most efficient regular tiling of the plane. The explanation goes that there is an evolutionary pressure for honeybees to conserve wax in the construction of there combs, so the efficiency of the hexagonal grid explains why it is selected for.[30]

The explanation based on the honeycomb conjecture is potentially incomplete because the proof is a solution to a tiling problem in two dimensions, and disregards the 3D structure of comb cells.[31] Furthermore, many mathematicians do not see the proof of the honeycomb conjecture as an explanatory proof as it employs concepts outside of geometry to establish a geometrical result.[32] It is also controversial amongst philosophers whether the subject matter of geometry is purely mathematical, or whether it concerns physical space and structures, leading them to question if the explanation is truly mathematical. However, as the proof does employ mathematics outside of geometry, Baker has argued that it is a genuinely mathematical explanation.[33] [this doesn't seem accurate about Baker - find something else to go here??]

There are also non-mathematical explanations for the honeycomb case study. Darwin believed that the hexagonal shape of bee combs was the result of tightly packed spherical cells being pushed together and pressed into hexagons, with bees fixing breakages with flat surfaces of wax further contributing to a hexagonal shape.[34] More modern presentations hold that the shape of honeycomb is due to the flow of molten wax during the construction process.[35]

Others

A 17th century map of Königsberg with its bridges and rivers highlighted
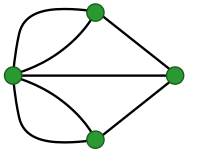
A graph representing the layout of bridges in Königsberg
Map of the seven bridges of Königsberg and their representation as a graph

Another key example is the Seven Bridges of Königsberg, which concerns the impossibility of crossing each of the historical seven bridges in the Prussian city of Königsberg a single time in a continuous walk around the city.[b] The explanation was found by Leonhard Euler in 1735 when he considered whether such a journey was possible.[36] Euler's solution involved abstracting away from the concrete details of the problem to a mathematical representation in the form of a graph, with nodes representing landmasses and lines representing bridges.[37] He reasoned that for each landmass, unless it is a starting or ending point, there must be a path to both enter and exit it. Therefore, there must be at most two nodes in the graph with an uneven number of lines connected to them for such a journey to be possible. But this is not the case for the graph representing the seven bridges in Königsberg, so it is mathematically impossible to cross all seven without crossing over one of the bridges multiple times.[38]

The existence at any particular time of antipodal points on the Earth's surface with equal temperature and pressure has been cited as another example. According to Colyvan, this is explained by the Borsuk–Ulam theorem, which entails that for any physical property that varies continuously across the surface of a sphere, there are antipodal points on that sphere with equal values of that property.[39] In response to this example, Baker has argued that it is a prediction rather than an explanation because antipodal points with equal pressure and temperature have not already been measured.[40] Mary Leng also questions whether it is appropriate to model temperature or pressure as continuous functions across individual points on the Earth's surface.[41][c]

An animation showing the phase-space trajectory of a Hénon-Heiles system. Poincaré section points (marked with crosses) form closed loops, showing that the system does not exhibit chaotic motion.

A key class of mathematical explanations is solutions to optimization problems, which includes the cicada and bee honeycomb case studies. In these cases, a certain feature is explained by showing that it is mathematically optimal.[43] Such explanations are important in evolutionary biology, as the mathematical demonstrations of optimality show why natural selection could not achieve a more optimal solution, but also appear in other areas of science such as physics, engineering and economics.[d] [cite rest of this]

A number of case studies draw from dynamical systems. Marc Lange, for example, argues that the fact that double pendulums always have four or more equilibrium configurations can be explained by the configuration space of the system forming the surface of a torus, which must have at least four stationary points.[44] Lyon and Colyvan point to the use of phase spaces and the Poincaré map to explain the behaviour of a Hénon–Heiles system, such as the stability of a star's orbit through a galaxy.[45] Other examples proposed by Colyvan include geometrical explanations for Lorentz contraction and gravitational lensing. Baker and Melia have objected to the geometrical aspects of these explanations, which could be interpreted physically instead of mathematically.[46]

Some examples are more mathematical. For example, widely discussed cases include the explanation for why 23 strawberries cannot be divided equally amongst three people,[47] why it is impossible to square the circle,[48] and why it is impossible to untie a trefoil knot.[49] However, it is unclear to what extent each of these cases are mathematical explanations of empirical phenomena rather than explanations internal to mathematics itself.[e] A key class of mathematical explanations is solutions to optimization problems, which includes the cicada and bee honeycomb case studies. [explain what they are] Other examples include sunflower seeds (?), marine predators & random walks, examples from economics. General features are.... Related - minimization processes, e.g. plateau soap film

[explain what they are] Other examples include sunflower seeds (?), marine predators & random walks, examples from economics. General features are.... Related - minimization processes, e.g. plateau soap film

Others that could be included: Kirkwood gaps

Include info on modal strength of mathematical explanations compared to non-mathematical explanations?




Maybe useful sources:

Barrantes 2019 - in depth analysis of periodic cicada case, some coverage of Bangu's circularity counter-argument, nominalized alternatives to Baker's explanation, discussion of theoretical virtues

Dieveney 2021 - discussion of the periodic cicada case, mainly around the fact that it relies on the idea that there are/were periodic predators for the cicadas which is unproven and adjustments made by Baker as a result, followed by an alternative example from Dieveney

Wójtowicz 2020 p. 185 - brief discussion of a number of different cases (antipodes, marine predatory behaviour, double pendulums, honeycomb, periodic cicadas, seven bridges in Königsberg) - afterwards there is discussion of the role of mathematical proof in explanations

Bangu 2012 p. 152 onwards - brief discussion of a few cases (antipodes, phase spaces, Lorentz contraction, periodic cicadas) followed by a bit on explanatory virtues and more extended section of periodic cicadas - then there is an alternative example by Bangu

Wakil & Justus 2017 - Extended discussion of periodic cicadas and bee honeycomb

Baron 2014 - Discussion of periodic cicadas, bee honeycomb and an example from Baron (marine predators), according to Baron the explanations are all solutions to optimality problems which are likely to be common in science (hence can't do piecemeal nominalizations without falling into the hard road) - further discussion of marine predator case by Baron here (alongside discussion of idealisations)

Saatsi 2011 - Extended discussion of periodic cicadas and bee honeycomb, arguing that mathematics in each is playing a representational rather than explanatory role

Saatsi 2017 - Extended discussion of explanatory power of phase spaces and dynamical systems

Raz 2013, 2017 - very detailed discussion of bee honeycomb case

Târziu 2018b - good coverage of cicada, honeycomb and antipodes cases

Cellucci 2017 - discussion of honeycomb, cicada and seven bridges in Königsberg cases

Drekalovic 2019 - cicada and Königsberg cases

Leng 2005 - general overview of mathematical explanation - early coverage of cicadas, antipodes and squaring the circle cases

Mathematical explanation

The philosophical study of mathematical explanations in science dates back to Aristotle, but within analytic philosophy, the first philosopher to deal with the issue was Mark Steiner, beginning in the 1970s.[53] [include quick description of Steiner's view?] Since then, there has been increasing attention on the question, and the explanatory indispensability argument has coincided with a greater emphasis on issues within the philosophy of mathematical practice more generally.[54] As a result, a number of competing theories of mathematical explanation have arisen, some favouring the argument and others contradicting it. [SEP maybe?]

[Cite all this]

Theories of mathematical explanation

Maybe useful sources: Wójtowicz 2020, Saatsi 2016

Talk about general features of case studies here? e.g. modal strength

Objections

The main response to the explanatory indispensability argument, adopted by philosophers such as Melia, Chris Daly, Simon Langford, and Juha Saatsi, is to deny there are genuinely mathematical explanations of empirical phenomena, instead framing the role of mathematics as representational or indexical. [cite + discuss this]

Others, particularly mathematical fictionalists such as Mary Leng and Stephen Yablo, have accepted that mathematics plays a genuinely explanatory role in science but argue that fictions can play an explanatory role. They point to the use of idealizations within science which explain empirical phenomena... [probably give example + cite] (Paseau & Baker section 6.2, Bangu section 9.4)

An objection advanced by Bangu states that the explanatory indispensability argument is circular and so begs the question in favour of its conclusion. Bangu argues that examples such as the periodic cicada case aim to explain statements that already contain mathematical content, namely the primeness of the cicadas life cycles. But an inference to the best explanation assumes that the statement being explained is true, and so inclusion of mathematical concepts such as primeness assume the truth of the mathematics in question.[55][f] Baker has responded to this objection by arguing that the statements being explained in such case studies can be reformulated to remove reference to mathematical entities, leaving mathematics indispensable only to the explanation itself and not the thing being explained.[57] (Baker 2021 discusses a section of PhD dissertation by David Michael Price arguing that circularity can be extended to all cases of mathematical explanation - room to include this directly in prose with mention of Steiner too?)

Notes

  1. ^ Also known as the enhanced indispensability argument[1] or explanationist indispensability argument[2]
  2. ^ Sometimes the additional requirement that the journey must begin and end at the same place is posed as part of the problem.
  3. ^ According to Jha et al. "continuity of temperature is ... a contingent causal phenomenon that depends on various factors, such as the vapor pressure of the droplets evaporating in the atmosphere; their interfacial conditions, including surface contamination; and so on".[42]
  4. ^ Optimization explanations in biology include sunflower seeds being arranged in the most space-efficient pattern and marine predators engaging in Levy walks because they minimize the average energy consumption required to find prey. [Add example from other areas of science?] Related to optimization explanations are explanations regarding minimization processes, such as the explanation of the shape of soap films from Plateau's laws which show that they minimize surface area.
  5. ^ Attributed to multiple sources: strawberry case study,[50] squaring the circle case study,[51] trefoil knot case study.[52]
  6. ^ A similar argument can be found from Steiner, who in 1978 claimed that "no explanatory argument can establish the existence of mathematical entities". According to Steiner, any description of the world necessarily presupposes the existence of mathematics, so it is impossible to compare mathematical explanations and non-mathematical explanations.[56]

References

Citations

  1. ^ Baker 2016, p. 225.
  2. ^ Hunt 2016, pp. 452–453; Bangu 2012, pp. 150–151, see also note 8 on p. 226.
  3. ^ Colyvan 2023, Introduction.
  4. ^ Drekalović & Žarnić 2018, p. 121; Molinini 2016, p. 404; Saatsi 2016, p. 1046.
  5. ^ Molinini, Pataut & Sereni 2016, p. 318.
  6. ^ Colyvan 2023, Introduction and §1.
  7. ^ Colyvan 2023, §3.
  8. ^ Colyvan 2023, §§4–5; Boyce 2021, p. 584.
  9. ^ Târziu 2018a, p. 396; Bangu 2012, pp. 147–148; Baron 2014, p. 460.
  10. ^ Heylen & Tump 2021, p. 3034; Lyon 2012, p. 572.
  11. ^ Heylen & Tump 2021, p. 3034; Lyon 2012, p. 572; Mancosu, Poggiolesi & Pincock 2023, §1.4.
  12. ^ Târziu 2018a, pp. 396–397.
  13. ^ Molinini, Pataut & Sereni 2016, p. 320; Bangu 2012, p. 150.
  14. ^ Marcus 2015, p. 127.
  15. ^ Bangu 2012, p. 150.
  16. ^ Marcus 2015, pp. 127–130.
  17. ^ Marcus 2015, p. 130.
  18. ^ Mancosu, Poggiolesi & Pincock 2023, §1.4.
  19. ^ Marcus n.d., §5.
  20. ^ Colyvan 2023, Bibliography; Colyvan & Resnik 2023.
  21. ^ Paseau & Baker 2023, p. 34.
  22. ^ Molinini, Pataut & Sereni 2016, p. 320; Baker 2005.
  23. ^ Barrantes 2019, p. 250; Leng 2005, pp. 184–185.
  24. ^ Colyvan 2023, §5; Paseau & Baker 2023, pp. 35–36.
  25. ^ Wakil & Justus 2017, pp. 918–919.
  26. ^ Barrantes 2019, pp. 251–253; McCullough-Benner 2022, pp. 754–758; Saatsi 2011, p. 150.
  27. ^ Dieveney 2021, p. 60; Drekalović 2019, p. 34.
  28. ^ Dieveney 2021, p. 60.
  29. ^ Dieveney 2021, p. 61.
  30. ^ Baron 2014, pp. 461–462; Räz 2013, pp. 351–352; Lyon & Colyvan 2008.
  31. ^ Wakil & Justus 2017, p. 923; Cellucci 2017, p. 22; Räz 2013.
  32. ^ Baker 2015, pp. 237–239.
  33. ^ Baron 2014, p. 462.
  34. ^ Wakil & Justus 2017, p. 921.
  35. ^ Wakil & Justus 2017, p. 922; Cellucci 2017, p. 22.
  36. ^ Lange 2013, pp. 488–489; Räz 2018, pp. 331–332; Pincock 2007.
  37. ^ Drekalović 2019, pp. 25–26; Vineberg 2018, p. 240.
  38. ^ Lange 2013, p. 489; Pantsar 2021, pp. 2595–2596; Vineberg 2018, p. 240.
  39. ^ Leng 2005, p. 181; Târziu 2018b, p. 93; Colyvan 2001, p. 49.
  40. ^ Marcus 2015, p. 131; Târziu 2018b, p. 93.
  41. ^ Marcus 2015, p. 131; Leng 2005, pp. 181–182.
  42. ^ Jha et al. 2024, p. 8.
  43. ^ Baker 2015, p. 241.
  44. ^ Pincock 2023, pp. 48–49; Jha et al. 2022; Lange 2013.
  45. ^ Saatsi 2017, pp. 894–895; Friend & Molinini 2016, pp. 188–189; Lyon & Colyvan 2008.
  46. ^ Marcus 2015, pp. 130–131; Saatsi 2007, p. 30; Sereni 2016, p. 426; Colyvan 2001, §3.3.
  47. ^ Baker 2021b, pp. 2–4; Bueno & French 2018, pp. 163–164; Lange 2013.
  48. ^ Leng 2005, pp. 182–184; Colyvan 2007.
  49. ^ Târziu 2018c, p. 474; Jha et al. 2024, pp. 16–17; Lange 2013.
  50. ^ Baker 2021b, pp. 2–4; Bueno & French 2018, pp. 163–164.
  51. ^ Leng 2005, pp. 182–184.
  52. ^ Târziu 2018c, p. 474; Jha et al. 2024, pp. 16–17.
  53. ^ Mancosu 2008, §5.1; Molinini, Pataut & Sereni 2016, p. 322.
  54. ^ Paseau & Baker 2023, p. 52; Molinini, Pataut & Sereni 2016, p. 323.
  55. ^ Mancosu, Poggiolesi & Pincock 2023, §1.4; Baker 2021a, p. 157; Heylen & Tump 2021, pp. 3055–3056.
  56. ^ Mancosu, Poggiolesi & Pincock 2023, §1.4; Mancosu 2008, p. 135; Steiner 1978b, pp. 19–20.
  57. ^ Heylen & Tump 2021, p. 3036; Baron 2020, pp. 20–21.

Sources

  • Baker, Alan (2005). "Are There Genuine Mathematical Explanations of Physical Phenomena?". Mind. 114 (454): 223–238. doi:10.1093/mind/fzi223. ISSN 0026-4423.
  • Baker, Alan (2009). "Mathematical Explanation in Science". The British Journal for the Philosophy of Science. 60 (3): 611–633. doi:10.1093/bjps/axp025. ISSN 0007-0882.
  • Baker, Alan (2015). "Mathematical Explanation in Biology". In Braillard, Pierre-Alain; Malaterre, Christophe (eds.). Explanation in Biology: An Enquiry into the Diversity of Explanatory Patterns in the Life Sciences. Springer Nature. pp. 229–247. ISBN 978-94-017-9821-1.
  • Baker, Alan (2016). "Non-Optional Projects: Mathematical and Ethical". In Leibowitz, Uri D.; Sinclair, Neil (eds.). Explanation in Ethics and Mathematics: Debunking and Dispensability. Oxford University Press. pp. 220–235. ISBN 9780198778592 – via Swarthmore College.
  • Baker, Alan (2021a). "Circularity, Indispensability, and Mathematical Explanation in Science". Studies in History and Philosophy of Science. 88: 156–163. doi:10.1016/j.shpsa.2021.05.017. ISSN 0039-3681.
  • Baker, Alan (2021b). "Bipedal Gait Costs: A New Case Study of Mathematical Explanation in Science". European Journal for Philosophy of Science. 11 (3). doi:10.1007/s13194-021-00411-3. ISSN 1879-4912.
  • Bangu, Sorin (2012). The Applicability of Mathematics in Science: Indispensability and Ontology. New Directions in the Philosophy of Science. Palgrave Macmillan. ISBN 978-0-230-28520-0.
  • Baron, Sam (2014). "Optimisation and Mathematical Explanation: Doing the Lévy Walk". Synthese. 191 (3): 459–479. doi:10.1007/s11229-013-0284-2. ISSN 0039-7857.
  • Baron, Sam (2020). "Purely Physical Explananda: Bistability in Perception". In Falguera, José L.; Martínez-Vidal, Concha (eds.). Abstract Objects: For and Against. Springer Nature. pp. 17–34. ISBN 978-3-030-38244-5.
  • Barrantes, Manuel (2019). "Optimal Representations and the Enhanced Indispensability Argument". Synthese. 196 (1): 247–263. doi:10.1007/s11229-017-1470-4. ISSN 0039-7857.
  • Boyce, Kenneth (2021). "Why Inference to the Best Explanation Doesn't Secure Empirical Grounds for Mathematical Platonism". Synthese. 198 (1): 583–595. doi:10.1007/s11229-018-02043-2. ISSN 0039-7857.
  • Bueno, Otávio; French, Steven (2018). "Explaining with Mathematics? From Cicadas to Symmetry". Applying Mathematics: Immersion, Inference, Interpretation. Oxford University Press. pp. 151–182. ISBN 978-0-19-881504-4.
  • Cellucci, Carlo (2017). "Mathematical Explanations". Rethinking Knowledge: The Heuristic View. European Studies in Philosophy of Science. Vol. 4. Springer. pp. 315–334. ISBN 978-3-319-53237-0.
Retrieved from "https://en.wikipedia.org/w/index.php?title=User:Shapeyness/sandbox/Explanatory_indispensability_argument&oldid=1221253053"