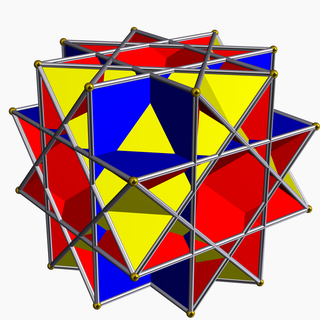
Nonconvex great rhombicuboctahedron
| Nonconvex great rhombicuboctahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 26, E = 48 V = 24 (χ = 2) |
| Faces by sides | 8{3}+(6+12){4} |
| Coxeter diagram |      
|
| Wythoff symbol | 3/2 4 | 2 3 4/3 | 2 |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U17, C59, W85 |
| Dual polyhedron | Great deltoidal icositetrahedron |
| Vertex figure |  4.4.4.3/2 |
| Bowers acronym | Querco |
In geometry, the nonconvex great rhombicuboctahedron is a nonconvex uniform polyhedron, indexed as U17. It has 26 faces (8 triangles and 18 squares), 48 edges, and 24 vertices.[1] It is represented by Schläfli symbol t0,2{4,3⁄2} and Coxeter-Dynkin diagram of 
. Its vertex figure is a crossed quadrilateral.
This model shares the name with the convex great rhombicuboctahedron, also called the truncated cuboctahedron.
An alternate name for this figure is quasirhombicuboctahedron. From that derives its Bowers acronym: querco.
Orthogonal projections
Cartesian coordinates
Cartesian coordinates for the vertices of a nonconvex great rhombicuboctahedron centered at the origin with edge length 1 are all the permutations of
- (±ξ, ±1, ±1),
where ξ = √2 − 1.
Related polyhedra
It shares the vertex arrangement with the convex truncated cube. It additionally shares its edge arrangement with the great cubicuboctahedron (having the triangular faces and 6 square faces in common), and with the great rhombihexahedron (having 12 square faces in common). It has the same vertex figure as the pseudo great rhombicuboctahedron, which is not a uniform polyhedron.
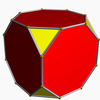 Truncated cube |
Great rhombicuboctahedron |
 Great cubicuboctahedron |
 Great rhombihexahedron |
 Pseudo great rhombicuboctahedron |
Great deltoidal icositetrahedron
| Great deltoidal icositetrahedron | |
|---|---|
| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 24, E = 48 V = 26 (χ = 2) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU17 |
| dual polyhedron | Nonconvex great rhombicuboctahedron |
The great deltoidal icositetrahedron is the dual of the nonconvex great rhombicuboctahedron.
References
- ^ Maeder, Roman. "17: great rhombicuboctahedron". MathConsult.
{{cite web}}: CS1 maint: url-status (link)
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208
External links
Weisstein, Eric W. "Great Deltoidal Icositetrahedron". MathWorld.
- Weisstein, Eric W. "Uniform great rhombicuboctahedron". MathWorld.
- Great Rhombicuboctahedron Paper model
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |